LAMBDA: A Large Model Based Data Agent

We introduce ``LAMBDA," a novel open-source, code-free multi-agent data analysis system that that harnesses the power of large models. LAMBDA is designed to address data analysis challenges in complex data-driven applications through the use of innovatively designed data agents that operate iteratively and generatively using natural language. At the core of LAMBDA are two key agent roles: the programmer and the inspector, which are engineered to work together seamlessly. Specifically, the programmer generates code based on the user's instructions and domain-specific knowledge, enhanced by advanced models. Meanwhile, the inspector debugs the code when necessary. To ensure robustness and handle adverse scenarios, LAMBDA features a user interface that allows direct user intervention in the operational loop. Additionally, LAMBDA can flexibly integrate external models and algorithms through our knowledge integration mechanism, catering to the needs of customized data analysis. LAMBDA has demonstrated strong performance on various machine learning datasets. It has the potential to enhance data science practice and analysis paradigm by seamlessly integrating human and artificial intelligence, making it more accessible, effective, and efficient for individuals from diverse backgrounds. The strong performance of LAMBDA in solving data science problems is demonstrated in several case studies, which are presented at \url{https://www.polyu.edu.hk/ama/cmfai/lambda.html}.

Machine Learning Insides OptVerse AI Solver: Design Principles and Applications

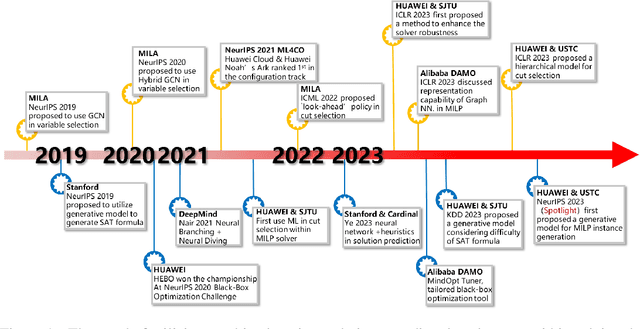
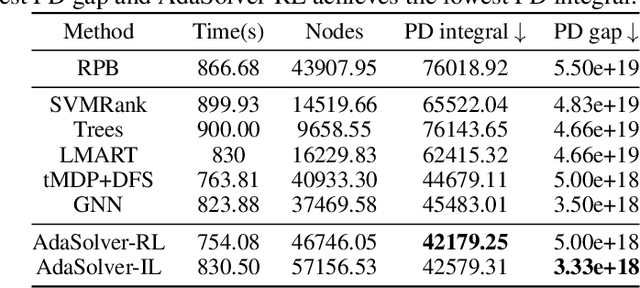
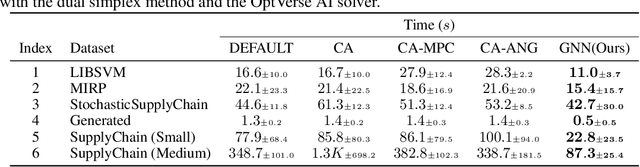
In an era of digital ubiquity, efficient resource management and decision-making are paramount across numerous industries. To this end, we present a comprehensive study on the integration of machine learning (ML) techniques into Huawei Cloud's OptVerse AI Solver, which aims to mitigate the scarcity of real-world mathematical programming instances, and to surpass the capabilities of traditional optimization techniques. We showcase our methods for generating complex SAT and MILP instances utilizing generative models that mirror multifaceted structures of real-world problem. Furthermore, we introduce a training framework leveraging augmentation policies to maintain solvers' utility in dynamic environments. Besides the data generation and augmentation, our proposed approaches also include novel ML-driven policies for personalized solver strategies, with an emphasis on applications like graph convolutional networks for initial basis selection and reinforcement learning for advanced presolving and cut selection. Additionally, we detail the incorporation of state-of-the-art parameter tuning algorithms which markedly elevate solver performance. Compared with traditional solvers such as Cplex and SCIP, our ML-augmented OptVerse AI Solver demonstrates superior speed and precision across both established benchmarks and real-world scenarios, reinforcing the practical imperative and effectiveness of machine learning techniques in mathematical programming solvers.

Randomly Projected Convex Clustering Model: Motivation, Realization, and Cluster Recovery Guarantees

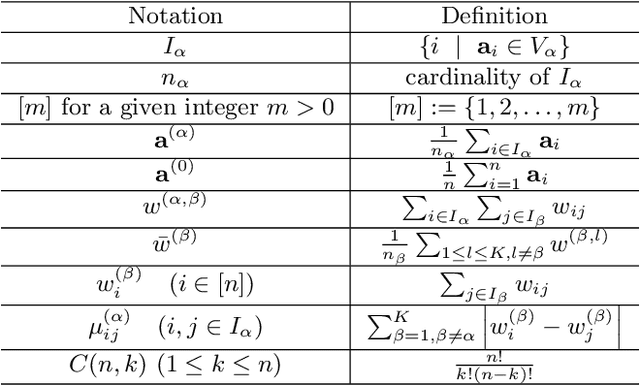
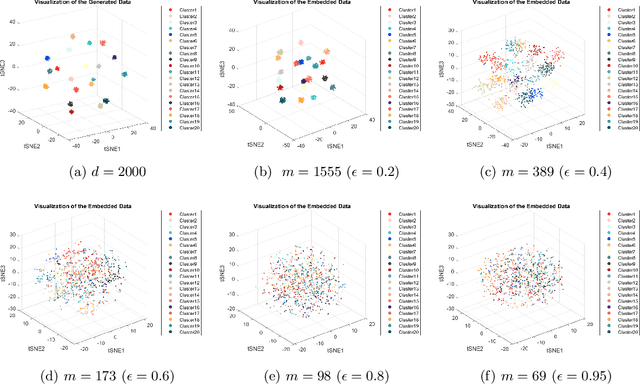
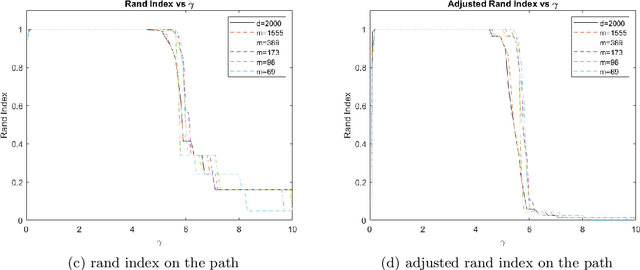
In this paper, we propose a randomly projected convex clustering model for clustering a collection of $n$ high dimensional data points in $\mathbb{R}^d$ with $K$ hidden clusters. Compared to the convex clustering model for clustering original data with dimension $d$, we prove that, under some mild conditions, the perfect recovery of the cluster membership assignments of the convex clustering model, if exists, can be preserved by the randomly projected convex clustering model with embedding dimension $m = O(\epsilon^{-2}\log(n))$, where $0 < \epsilon < 1$ is some given parameter. We further prove that the embedding dimension can be improved to be $O(\epsilon^{-2}\log(K))$, which is independent of the number of data points. Extensive numerical experiment results will be presented in this paper to demonstrate the robustness and superior performance of the randomly projected convex clustering model. The numerical results presented in this paper also demonstrate that the randomly projected convex clustering model can outperform the randomly projected K-means model in practice.

Beyond ADMM: A Unified Client-variance-reduced Adaptive Federated Learning Framework

As a novel distributed learning paradigm, federated learning (FL) faces serious challenges in dealing with massive clients with heterogeneous data distribution and computation and communication resources. Various client-variance-reduction schemes and client sampling strategies have been respectively introduced to improve the robustness of FL. Among others, primal-dual algorithms such as the alternating direction of method multipliers (ADMM) have been found being resilient to data distribution and outperform most of the primal-only FL algorithms. However, the reason behind remains a mystery still. In this paper, we firstly reveal the fact that the federated ADMM is essentially a client-variance-reduced algorithm. While this explains the inherent robustness of federated ADMM, the vanilla version of it lacks the ability to be adaptive to the degree of client heterogeneity. Besides, the global model at the server under client sampling is biased which slows down the practical convergence. To go beyond ADMM, we propose a novel primal-dual FL algorithm, termed FedVRA, that allows one to adaptively control the variance-reduction level and biasness of the global model. In addition, FedVRA unifies several representative FL algorithms in the sense that they are either special instances of FedVRA or are close to it. Extensions of FedVRA to semi/un-supervised learning are also presented. Experiments based on (semi-)supervised image classification tasks demonstrate superiority of FedVRA over the existing schemes in learning scenarios with massive heterogeneous clients and client sampling.

Learning Graph Laplacian with MCP

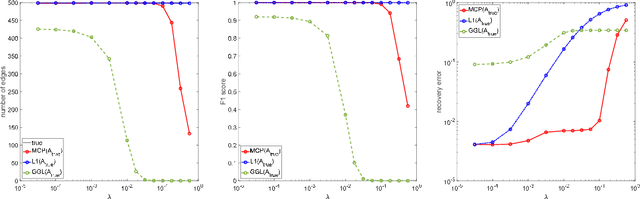
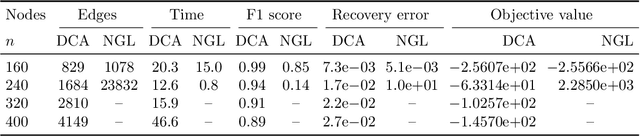
Motivated by the observation that the ability of the $\ell_1$ norm in promoting sparsity in graphical models with Laplacian constraints is much weakened, this paper proposes to learn graph Laplacian with a non-convex penalty: minimax concave penalty (MCP). For solving the MCP penalized graphical model, we design an inexact proximal difference-of-convex algorithm (DCA) and prove its convergence to critical points. We note that each subproblem of the proximal DCA enjoys the nice property that the objective function in its dual problem is continuously differentiable with a semismooth gradient. Therefore, we apply an efficient semismooth Newton method to subproblems of the proximal DCA. Numerical experiments on various synthetic and real data sets demonstrate the effectiveness of the non-convex penalty MCP in promoting sparsity. Compared with the state-of-the-art method \cite[Algorithm~1]{ying2020does}, our method is demonstrated to be more efficient and reliable for learning graph Laplacian with MCP.

Estimation of sparse Gaussian graphical models with hidden clustering structure

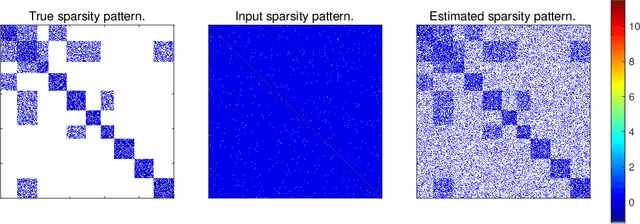
Estimation of Gaussian graphical models is important in natural science when modeling the statistical relationships between variables in the form of a graph. The sparsity and clustering structure of the concentration matrix is enforced to reduce model complexity and describe inherent regularities. We propose a model to estimate the sparse Gaussian graphical models with hidden clustering structure, which also allows additional linear constraints to be imposed on the concentration matrix. We design an efficient two-phase algorithm for solving the proposed model. We develop a symmetric Gauss-Seidel based alternating direction method of the multipliers (sGS-ADMM) to generate an initial point to warm-start the second phase algorithm, which is a proximal augmented Lagrangian method (pALM), to get a solution with high accuracy. Numerical experiments on both synthetic data and real data demonstrate the good performance of our model, as well as the efficiency and robustness of our proposed algorithm.

Efficient algorithms for multivariate shape-constrained convex regression problems

Shape-constrained convex regression problem deals with fitting a convex function to the observed data, where additional constraints are imposed, such as component-wise monotonicity and uniform Lipschitz continuity. This paper provides a comprehensive mechanism for computing the least squares estimator of a multivariate shape-constrained convex regression function in $\mathbb{R}^d$. We prove that the least squares estimator is computable via solving a constrained convex quadratic programming (QP) problem with $(n+1)d$ variables and at least $n(n-1)$ linear inequality constraints, where $n$ is the number of data points. For solving the generally very large-scale convex QP, we design two efficient algorithms, one is the symmetric Gauss-Seidel based alternating direction method of multipliers ({\tt sGS-ADMM}), and the other is the proximal augmented Lagrangian method ({\tt pALM}) with the subproblems solved by the semismooth Newton method ({\tt SSN}). Comprehensive numerical experiments, including those in the pricing of basket options and estimation of production functions in economics, demonstrate that both of our proposed algorithms outperform the state-of-the-art algorithm. The {\tt pALM} is more efficient than the {\tt sGS-ADMM} but the latter has the advantage of being simpler to implement.

A sparse semismooth Newton based proximal majorization-minimization algorithm for nonconvex square-root-loss regression problems

In this paper, we consider high-dimensional nonconvex square-root-loss regression problems and introduce a proximal majorization-minimization (PMM) algorithm for these problems. Our key idea for making the proposed PMM to be efficient is to develop a sparse semismooth Newton method to solve the corresponding subproblems. By using the Kurdyka-{\L}ojasiewicz property exhibited in the underlining problems, we prove that the PMM algorithm converges to a d-stationary point. We also analyze the oracle property of the initial subproblem used in our algorithm. Extensive numerical experiments are presented to demonstrate the high efficiency of the proposed PMM algorithm.

On the Closed-form Proximal Mapping and Efficient Algorithms for Exclusive Lasso Models

The exclusive lasso regularization based on the $\ell_{1,2}$ norm has become popular recently due to its superior performance over the group lasso regularization. Comparing to the group lasso regularization which enforces the competition on variables among different groups and results in inter-group sparsity, the exclusive lasso regularization also enforces the competition within each group and results in intra-group sparsity. However, to the best of our knowledge, a correct closed-form solution to the proximal mapping of the $\ell_{1,2}$ norm has still been elusive. In this paper, we fill the gap by deriving a closed-form solution for $\rm{Prox}_{\rho\|\cdot\|_1^2}(\cdot)$ and its generalized Jacobian. Based on the obtained analytical results, we are able to design efficient first and second order algorithms for machine learning models involving the exclusive lasso regularization. Our analytical solution of the proximal mapping for the exclusive lasso regularization can be used to improve the efficiency of existing algorithms relying on the efficient computation of the proximal mapping.

A Fast Globally Linearly Convergent Algorithm for the Computation of Wasserstein Barycenters

In this paper, we consider the problem of computing a Wasserstein barycenter for a set of discrete probability distributions with finite supports, which finds many applications in different areas such as statistics, machine learning and image processing. When the support points of the barycenter are pre-specified, this problem can be modeled as a linear programming (LP), while the problem size can be extremely large. To handle this large-scale LP, in this paper, we derive its dual problem, which is conceivably more tractable and can be reformulated as a well-structured convex problem with 3 kinds of block variables and a coupling linear equality constraint. We then adapt a symmetric Gauss-Seidel based alternating direction method of multipliers (sGS-ADMM) to solve the resulting dual problem and analyze its global convergence as well as its global linear convergence rate. We also show how all the subproblems involved can be solved exactly and efficiently. This makes our method suitable for computing a Wasserstein barycenter on a large dataset. In addition, our sGS-ADMM can be used as a subroutine in an alternating minimization method to compute a barycenter when its support points are not pre-specified. Numerical results on synthetic datasets and image datasets demonstrate that our method is more efficient for solving large-scale problems, comparing with two existing representative methods and the commercial software Gurobi.