Approximation Bounds for Transformer Networks with Application to Regression

We explore the approximation capabilities of Transformer networks for H\"older and Sobolev functions, and apply these results to address nonparametric regression estimation with dependent observations. First, we establish novel upper bounds for standard Transformer networks approximating sequence-to-sequence mappings whose component functions are H\"older continuous with smoothness index $\gamma \in (0,1]$. To achieve an approximation error $\varepsilon$ under the $L^p$-norm for $p \in [1, \infty]$, it suffices to use a fixed-depth Transformer network whose total number of parameters scales as $\varepsilon^{-d_x n / \gamma}$. This result not only extends existing findings to include the case $p = \infty$, but also matches the best known upper bounds on number of parameters previously obtained for fixed-depth FNNs and RNNs. Similar bounds are also derived for Sobolev functions. Second, we derive explicit convergence rates for the nonparametric regression problem under various $\beta$-mixing data assumptions, which allow the dependence between observations to weaken over time. Our bounds on the sample complexity impose no constraints on weight magnitudes. Lastly, we propose a novel proof strategy to establish approximation bounds, inspired by the Kolmogorov-Arnold representation theorem. We show that if the self-attention layer in a Transformer can perform column averaging, the network can approximate sequence-to-sequence H\"older functions, offering new insights into the interpretability of self-attention mechanisms.

Error Analysis of Three-Layer Neural Network Trained with PGD for Deep Ritz Method

Machine learning is a rapidly advancing field with diverse applications across various domains. One prominent area of research is the utilization of deep learning techniques for solving partial differential equations(PDEs). In this work, we specifically focus on employing a three-layer tanh neural network within the framework of the deep Ritz method(DRM) to solve second-order elliptic equations with three different types of boundary conditions. We perform projected gradient descent(PDG) to train the three-layer network and we establish its global convergence. To the best of our knowledge, we are the first to provide a comprehensive error analysis of using overparameterized networks to solve PDE problems, as our analysis simultaneously includes estimates for approximation error, generalization error, and optimization error. We present error bound in terms of the sample size $n$ and our work provides guidance on how to set the network depth, width, step size, and number of iterations for the projected gradient descent algorithm. Importantly, our assumptions in this work are classical and we do not require any additional assumptions on the solution of the equation. This ensures the broad applicability and generality of our results.

Convergence Analysis of Flow Matching in Latent Space with Transformers

We present theoretical convergence guarantees for ODE-based generative models, specifically flow matching. We use a pre-trained autoencoder network to map high-dimensional original inputs to a low-dimensional latent space, where a transformer network is trained to predict the velocity field of the transformation from a standard normal distribution to the target latent distribution. Our error analysis demonstrates the effectiveness of this approach, showing that the distribution of samples generated via estimated ODE flow converges to the target distribution in the Wasserstein-2 distance under mild and practical assumptions. Furthermore, we show that arbitrary smooth functions can be effectively approximated by transformer networks with Lipschitz continuity, which may be of independent interest.

Convergence Analysis of the Deep Galerkin Method for Weak Solutions

This paper analyzes the convergence rate of a deep Galerkin method for the weak solution (DGMW) of second-order elliptic partial differential equations on $\mathbb{R}^d$ with Dirichlet, Neumann, and Robin boundary conditions, respectively. In DGMW, a deep neural network is applied to parametrize the PDE solution, and a second neural network is adopted to parametrize the test function in the traditional Galerkin formulation. By properly choosing the depth and width of these two networks in terms of the number of training samples $n$, it is shown that the convergence rate of DGMW is $\mathcal{O}(n^{-1/d})$, which is the first convergence result for weak solutions. The main idea of the proof is to divide the error of the DGMW into an approximation error and a statistical error. We derive an upper bound on the approximation error in the $H^{1}$ norm and bound the statistical error via Rademacher complexity.

Deep Neural Networks with ReLU-Sine-Exponential Activations Break Curse of Dimensionality on Hölder Class

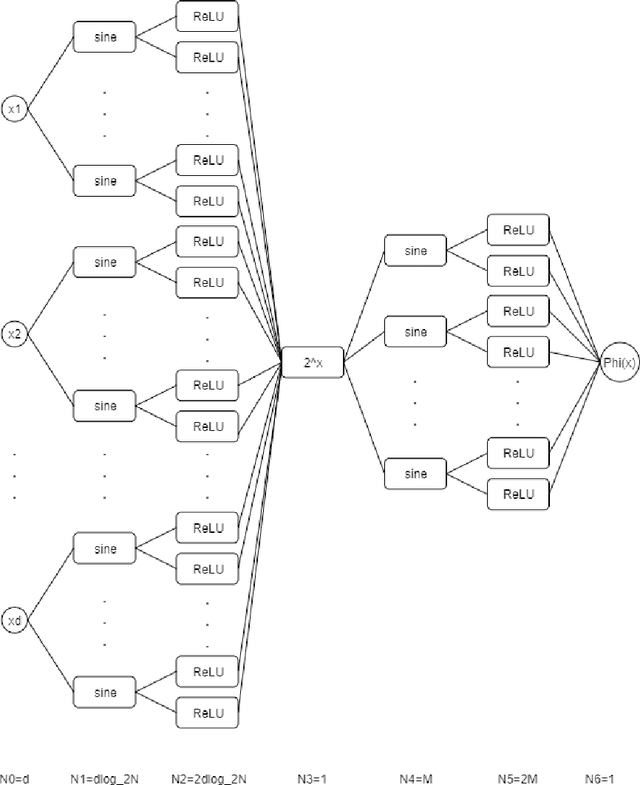
In this paper, we construct neural networks with ReLU, sine and $2^x$ as activation functions. For general continuous $f$ defined on $[0,1]^d$ with continuity modulus $\omega_f(\cdot)$, we construct ReLU-sine-$2^x$ networks that enjoy an approximation rate $\mathcal{O}(\omega_f(\sqrt{d})\cdot2^{-M}+\omega_{f}\left(\frac{\sqrt{d}}{N}\right))$, where $M,N\in \mathbb{N}^{+}$ denote the hyperparameters related to widths of the networks. As a consequence, we can construct ReLU-sine-$2^x$ network with the depth $5$ and width $\max\left\{\left\lceil2d^{3/2}\left(\frac{3\mu}{\epsilon}\right)^{1/{\alpha}}\right\rceil,2\left\lceil\log_2\frac{3\mu d^{\alpha/2}}{2\epsilon}\right\rceil+2\right\}$ that approximates $f\in \mathcal{H}_{\mu}^{\alpha}([0,1]^d)$ within a given tolerance $\epsilon >0$ measured in $L^p$ norm $p\in[1,\infty)$, where $\mathcal{H}_{\mu}^{\alpha}([0,1]^d)$ denotes the H\"older continuous function class defined on $[0,1]^d$ with order $\alpha \in (0,1]$ and constant $\mu > 0$. Therefore, the ReLU-sine-$2^x$ networks overcome the curse of dimensionality on $\mathcal{H}_{\mu}^{\alpha}([0,1]^d)$. In addition to its supper expressive power, functions implemented by ReLU-sine-$2^x$ networks are (generalized) differentiable, enabling us to apply SGD to train.