DeepTracer: Tracing Stolen Model via Deep Coupled Watermarks

Model watermarking techniques can embed watermark information into the protected model for ownership declaration by constructing specific input-output pairs. However, existing watermarks are easily removed when facing model stealing attacks, and make it difficult for model owners to effectively verify the copyright of stolen models. In this paper, we analyze the root cause of the failure of current watermarking methods under model stealing scenarios and then explore potential solutions. Specifically, we introduce a robust watermarking framework, DeepTracer, which leverages a novel watermark samples construction method and a same-class coupling loss constraint. DeepTracer can incur a high-coupling model between watermark task and primary task that makes adversaries inevitably learn the hidden watermark task when stealing the primary task functionality. Furthermore, we propose an effective watermark samples filtering mechanism that elaborately select watermark key samples used in model ownership verification to enhance the reliability of watermarks. Extensive experiments across multiple datasets and models demonstrate that our method surpasses existing approaches in defending against various model stealing attacks, as well as watermark attacks, and achieves new state-of-the-art effectiveness and robustness.

Sobolev norm inconsistency of kernel interpolation

We study the consistency of minimum-norm interpolation in reproducing kernel Hilbert spaces corresponding to bounded kernels. Our main result give lower bounds for the generalization error of the kernel interpolation measured in a continuous scale of norms that interpolate between $L^2$ and the hypothesis space. These lower bounds imply that kernel interpolation is always inconsistent, when the smoothness index of the norm is larger than a constant that depends only on the embedding index of the hypothesis space and the decay rate of the eigenvalues.

Enhancing Playback Performance in Video Recommender Systems with an On-Device Gating and Ranking Framework

Video recommender systems (RSs) have gained increasing attention in recent years. Existing mainstream RSs focus on optimizing the matching function between users and items. However, we noticed that users frequently encounter playback issues such as slow loading or stuttering while browsing the videos, especially in weak network conditions, which will lead to a subpar browsing experience, and may cause users to leave, even when the video content and recommendations are superior. It is quite a serious issue, yet easily overlooked. To tackle this issue, we propose an on-device Gating and Ranking Framework (GRF) that cooperates with server-side RS. Specifically, we utilize a gate model to identify videos that may have playback issues in real-time, and then we employ a ranking model to select the optimal result from a locally-cached pool to replace the stuttering videos. Our solution has been fully deployed on Kwai, a large-scale short video platform with hundreds of millions of users globally. Moreover, it significantly enhances video playback performance and improves overall user experience and retention rates.

On the optimal approximation of Sobolev and Besov functions using deep ReLU neural networks

This paper studies the problem of how efficiently functions in the Sobolev spaces $\mathcal{W}^{s,q}([0,1]^d)$ and Besov spaces $\mathcal{B}^s_{q,r}([0,1]^d)$ can be approximated by deep ReLU neural networks with width $W$ and depth $L$, when the error is measured in the $L^p([0,1]^d)$ norm. This problem has been studied by several recent works, which obtained the approximation rate $\mathcal{O}((WL)^{-2s/d})$ up to logarithmic factors when $p=q=\infty$, and the rate $\mathcal{O}(L^{-2s/d})$ for networks with fixed width when the Sobolev embedding condition $1/q -1/p<s/d$ holds. We generalize these results by showing that the rate $\mathcal{O}((WL)^{-2s/d})$ indeed holds under the Sobolev embedding condition. It is known that this rate is optimal up to logarithmic factors. The key tool in our proof is a novel encoding of sparse vectors by using deep ReLU neural networks with varied width and depth, which may be of independent interest.

On the rates of convergence for learning with convolutional neural networks

We study approximation and learning capacities of convolutional neural networks (CNNs) with one-side zero-padding and multiple channels. Our first result proves a new approximation bound for CNNs with certain constraint on the weights. Our second result gives new analysis on the covering number of feed-forward neural networks with CNNs as special cases. The analysis carefully takes into account the size of the weights and hence gives better bounds than the existing literature in some situations. Using these two results, we are able to derive rates of convergence for estimators based on CNNs in many learning problems. In particular, we establish minimax optimal convergence rates of the least squares based on CNNs for learning smooth functions in the nonparametric regression setting. For binary classification, we derive convergence rates for CNN classifiers with hinge loss and logistic loss. It is also shown that the obtained rates for classification are minimax optimal in some common settings.

Nonparametric regression using over-parameterized shallow ReLU neural networks

It is shown that over-parameterized neural networks can achieve minimax optimal rates of convergence (up to logarithmic factors) for learning functions from certain smooth function classes, if the weights are suitably constrained or regularized. Specifically, we consider the nonparametric regression of estimating an unknown $d$-variate function by using shallow ReLU neural networks. It is assumed that the regression function is from the H\"older space with smoothness $\alpha<(d+3)/2$ or a variation space corresponding to shallow neural networks, which can be viewed as an infinitely wide neural network. In this setting, we prove that least squares estimators based on shallow neural networks with certain norm constraints on the weights are minimax optimal, if the network width is sufficiently large. As a byproduct, we derive a new size-independent bound for the local Rademacher complexity of shallow ReLU neural networks, which may be of independent interest.

Optimal rates of approximation by shallow ReLU$^k$ neural networks and applications to nonparametric regression

We study the approximation capacity of some variation spaces corresponding to shallow ReLU$^k$ neural networks. It is shown that sufficiently smooth functions are contained in these spaces with finite variation norms. For functions with less smoothness, the approximation rates in terms of the variation norm are established. Using these results, we are able to prove the optimal approximation rates in terms of the number of neurons for shallow ReLU$^k$ neural networks. It is also shown how these results can be used to derive approximation bounds for deep neural networks and convolutional neural networks (CNNs). As applications, we study convergence rates for nonparametric regression using three ReLU neural network models: shallow neural network, over-parameterized neural network, and CNN. In particular, we show that shallow neural networks can achieve the minimax optimal rates for learning H\"older functions, which complements recent results for deep neural networks. It is also proven that over-parameterized (deep or shallow) neural networks can achieve nearly optimal rates for nonparametric regression.

Convergence Analysis of the Deep Galerkin Method for Weak Solutions

This paper analyzes the convergence rate of a deep Galerkin method for the weak solution (DGMW) of second-order elliptic partial differential equations on $\mathbb{R}^d$ with Dirichlet, Neumann, and Robin boundary conditions, respectively. In DGMW, a deep neural network is applied to parametrize the PDE solution, and a second neural network is adopted to parametrize the test function in the traditional Galerkin formulation. By properly choosing the depth and width of these two networks in terms of the number of training samples $n$, it is shown that the convergence rate of DGMW is $\mathcal{O}(n^{-1/d})$, which is the first convergence result for weak solutions. The main idea of the proof is to divide the error of the DGMW into an approximation error and a statistical error. We derive an upper bound on the approximation error in the $H^{1}$ norm and bound the statistical error via Rademacher complexity.

Universality and approximation bounds for echo state networks with random weights

We study the uniform approximation of echo state networks with randomly generated internal weights. These models, in which only the readout weights are optimized during training, have made empirical success in learning dynamical systems. We address the representational capacity of these models by showing that they are universal under weak conditions. Our main result gives a sufficient condition for the activation function and a sampling procedure for the internal weights so that echo state networks can approximate any continuous casual time-invariant operators with high probability. In particular, for ReLU activation, we quantify the approximation error of echo state networks for sufficiently regular operators.

Learning Distributions by Generative Adversarial Networks: Approximation and Generalization

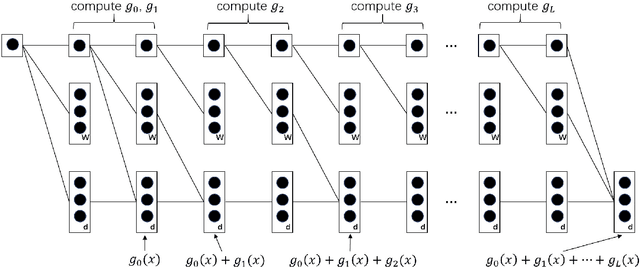
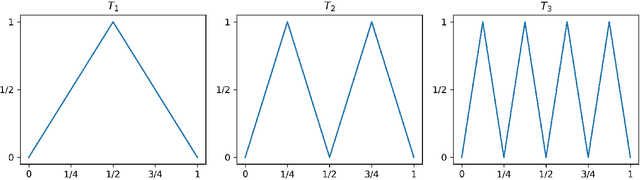
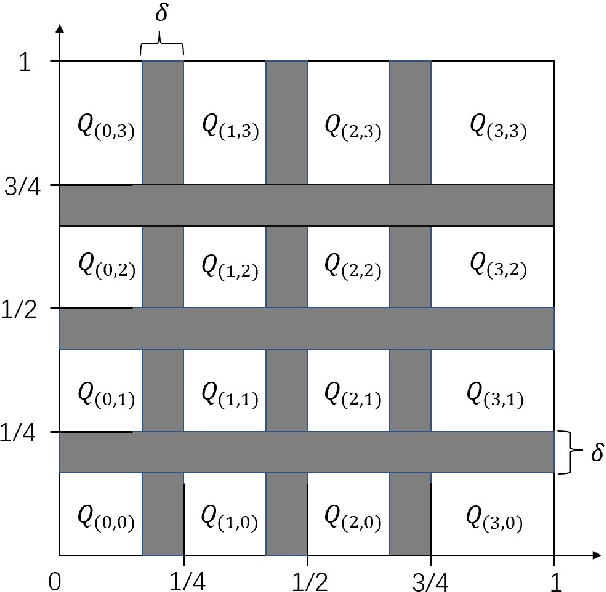
We study how well generative adversarial networks (GAN) learn probability distributions from finite samples by analyzing the convergence rates of these models. Our analysis is based on a new oracle inequality that decomposes the estimation error of GAN into the discriminator and generator approximation errors, generalization error and optimization error. To estimate the discriminator approximation error, we establish error bounds on approximating H\"older functions by ReLU neural networks, with explicit upper bounds on the Lipschitz constant of the network or norm constraint on the weights. For generator approximation error, we show that neural network can approximately transform a low-dimensional source distribution to a high-dimensional target distribution and bound such approximation error by the width and depth of neural network. Combining the approximation results with generalization bounds of neural networks from statistical learning theory, we establish the convergence rates of GANs in various settings, when the error is measured by a collection of integral probability metrics defined through H\"older classes, including the Wasserstein distance as a special case. In particular, for distributions concentrated around a low-dimensional set, we show that the convergence rates of GANs do not depend on the high ambient dimension, but on the lower intrinsic dimension.