Two-Stage Data Synthesization: A Statistics-Driven Restricted Trade-off between Privacy and Prediction

Synthetic data have gained increasing attention across various domains, with a growing emphasis on their performance in downstream prediction tasks. However, most existing synthesis strategies focus on maintaining statistical information. Although some studies address prediction performance guarantees, their single-stage synthesis designs make it challenging to balance the privacy requirements that necessitate significant perturbations and the prediction performance that is sensitive to such perturbations. We propose a two-stage synthesis strategy. In the first stage, we introduce a synthesis-then-hybrid strategy, which involves a synthesis operation to generate pure synthetic data, followed by a hybrid operation that fuses the synthetic data with the original data. In the second stage, we present a kernel ridge regression (KRR)-based synthesis strategy, where a KRR model is first trained on the original data and then used to generate synthetic outputs based on the synthetic inputs produced in the first stage. By leveraging the theoretical strengths of KRR and the covariant distribution retention achieved in the first stage, our proposed two-stage synthesis strategy enables a statistics-driven restricted privacy--prediction trade-off and guarantee optimal prediction performance. We validate our approach and demonstrate its characteristics of being statistics-driven and restricted in achieving the privacy--prediction trade-off both theoretically and numerically. Additionally, we showcase its generalizability through applications to a marketing problem and five real-world datasets.

Optimal Convergence Rates of Deep Neural Network Classifiers

In this paper, we study the binary classification problem on $[0,1]^d$ under the Tsybakov noise condition (with exponent $s \in [0,\infty]$) and the compositional assumption. This assumption requires the conditional class probability function of the data distribution to be the composition of $q+1$ vector-valued multivariate functions, where each component function is either a maximum value function or a H\"{o}lder-$\beta$ smooth function that depends only on $d_*$ of its input variables. Notably, $d_*$ can be significantly smaller than the input dimension $d$. We prove that, under these conditions, the optimal convergence rate for the excess 0-1 risk of classifiers is $$ \left( \frac{1}{n} \right)^{\frac{\beta\cdot(1\wedge\beta)^q}{{\frac{d_*}{s+1}+(1+\frac{1}{s+1})\cdot\beta\cdot(1\wedge\beta)^q}}}\;\;\;, $$ which is independent of the input dimension $d$. Additionally, we demonstrate that ReLU deep neural networks (DNNs) trained with hinge loss can achieve this optimal convergence rate up to a logarithmic factor. This result provides theoretical justification for the excellent performance of ReLU DNNs in practical classification tasks, particularly in high-dimensional settings. The technique used to establish these results extends the oracle inequality presented in our previous work. The generalized approach is of independent interest.

Super-fast rates of convergence for Neural Networks Classifiers under the Hard Margin Condition

We study the classical binary classification problem for hypothesis spaces of Deep Neural Networks (DNNs) with ReLU activation under Tsybakov's low-noise condition with exponent $q>0$, and its limit-case $q\to\infty$ which we refer to as the "hard-margin condition". We show that DNNs which minimize the empirical risk with square loss surrogate and $\ell_p$ penalty can achieve finite-sample excess risk bounds of order $\mathcal{O}\left(n^{-\alpha}\right)$ for arbitrarily large $\alpha>0$ under the hard-margin condition, provided that the regression function $\eta$ is sufficiently smooth. The proof relies on a novel decomposition of the excess risk which might be of independent interest.

Two-Dimensional Deep ReLU CNN Approximation for Korobov Functions: A Constructive Approach

This paper investigates approximation capabilities of two-dimensional (2D) deep convolutional neural networks (CNNs), with Korobov functions serving as a benchmark. We focus on 2D CNNs, comprising multi-channel convolutional layers with zero-padding and ReLU activations, followed by a fully connected layer. We propose a fully constructive approach for building 2D CNNs to approximate Korobov functions and provide rigorous analysis of the complexity of the constructed networks. Our results demonstrate that 2D CNNs achieve near-optimal approximation rates under the continuous weight selection model, significantly alleviating the curse of dimensionality. This work provides a solid theoretical foundation for 2D CNNs and illustrates their potential for broader applications in function approximation.

Spherical Analysis of Learning Nonlinear Functionals

In recent years, there has been growing interest in the field of functional neural networks. They have been proposed and studied with the aim of approximating continuous functionals defined on sets of functions on Euclidean domains. In this paper, we consider functionals defined on sets of functions on spheres. The approximation ability of deep ReLU neural networks is investigated by novel spherical analysis using an encoder-decoder framework. An encoder comes up first to accommodate the infinite-dimensional nature of the domain of functionals. It utilizes spherical harmonics to help us extract the latent finite-dimensional information of functions, which in turn facilitates in the next step of approximation analysis using fully connected neural networks. Moreover, real-world objects are frequently sampled discretely and are often corrupted by noise. Therefore, encoders with discrete input and those with discrete and random noise input are constructed, respectively. The approximation rates with different encoder structures are provided therein.

Convergence Analysis for Deep Sparse Coding via Convolutional Neural Networks

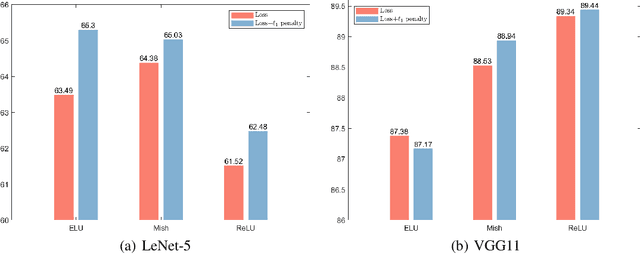
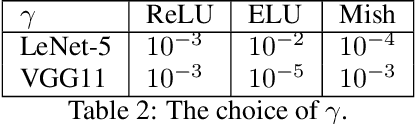
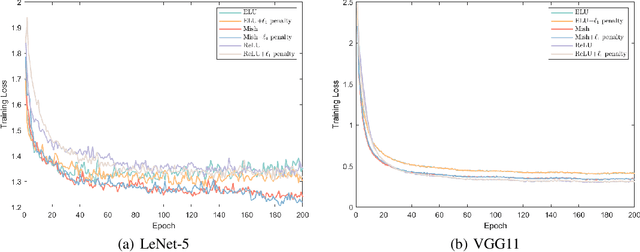
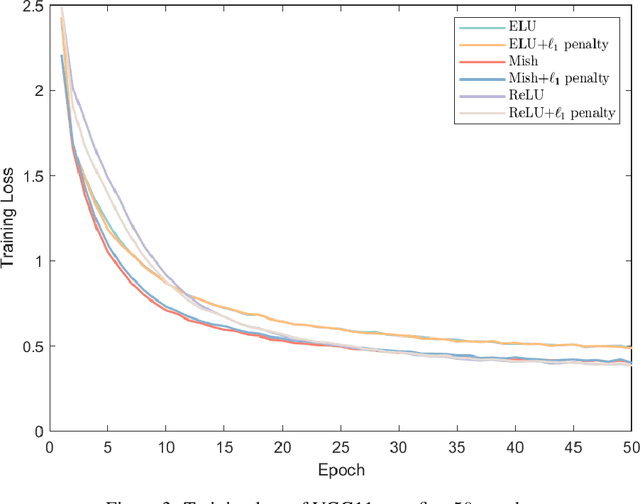
In this work, we explore the intersection of sparse coding theory and deep learning to enhance our understanding of feature extraction capabilities in advanced neural network architectures. We begin by introducing a novel class of Deep Sparse Coding (DSC) models and establish a thorough theoretical analysis of their uniqueness and stability properties. By applying iterative algorithms to these DSC models, we derive convergence rates for convolutional neural networks (CNNs) in their ability to extract sparse features. This provides a strong theoretical foundation for the use of CNNs in sparse feature learning tasks. We additionally extend this convergence analysis to more general neural network architectures, including those with diverse activation functions, as well as self-attention and transformer-based models. This broadens the applicability of our findings to a wide range of deep learning methods for deep sparse feature extraction. Inspired by the strong connection between sparse coding and CNNs, we also explore training strategies to encourage neural networks to learn more sparse features. Through numerical experiments, we demonstrate the effectiveness of these approaches, providing valuable insights for the design of efficient and interpretable deep learning models.

Bridging Smoothness and Approximation: Theoretical Insights into Over-Smoothing in Graph Neural Networks

In this paper, we explore the approximation theory of functions defined on graphs. Our study builds upon the approximation results derived from the $K$-functional. We establish a theoretical framework to assess the lower bounds of approximation for target functions using Graph Convolutional Networks (GCNs) and examine the over-smoothing phenomenon commonly observed in these networks. Initially, we introduce the concept of a $K$-functional on graphs, establishing its equivalence to the modulus of smoothness. We then analyze a typical type of GCN to demonstrate how the high-frequency energy of the output decays, an indicator of over-smoothing. This analysis provides theoretical insights into the nature of over-smoothing within GCNs. Furthermore, we establish a lower bound for the approximation of target functions by GCNs, which is governed by the modulus of smoothness of these functions. This finding offers a new perspective on the approximation capabilities of GCNs. In our numerical experiments, we analyze several widely applied GCNs and observe the phenomenon of energy decay. These observations corroborate our theoretical results on exponential decay order.

Generalization analysis with deep ReLU networks for metric and similarity learning

While considerable theoretical progress has been devoted to the study of metric and similarity learning, the generalization mystery is still missing. In this paper, we study the generalization performance of metric and similarity learning by leveraging the specific structure of the true metric (the target function). Specifically, by deriving the explicit form of the true metric for metric and similarity learning with the hinge loss, we construct a structured deep ReLU neural network as an approximation of the true metric, whose approximation ability relies on the network complexity. Here, the network complexity corresponds to the depth, the number of nonzero weights and the computation units of the network. Consider the hypothesis space which consists of the structured deep ReLU networks, we develop the excess generalization error bounds for a metric and similarity learning problem by estimating the approximation error and the estimation error carefully. An optimal excess risk rate is derived by choosing the proper capacity of the constructed hypothesis space. To the best of our knowledge, this is the first-ever-known generalization analysis providing the excess generalization error for metric and similarity learning. In addition, we investigate the properties of the true metric of metric and similarity learning with general losses.

On the rates of convergence for learning with convolutional neural networks

We study approximation and learning capacities of convolutional neural networks (CNNs) with one-side zero-padding and multiple channels. Our first result proves a new approximation bound for CNNs with certain constraint on the weights. Our second result gives new analysis on the covering number of feed-forward neural networks with CNNs as special cases. The analysis carefully takes into account the size of the weights and hence gives better bounds than the existing literature in some situations. Using these two results, we are able to derive rates of convergence for estimators based on CNNs in many learning problems. In particular, we establish minimax optimal convergence rates of the least squares based on CNNs for learning smooth functions in the nonparametric regression setting. For binary classification, we derive convergence rates for CNN classifiers with hinge loss and logistic loss. It is also shown that the obtained rates for classification are minimax optimal in some common settings.

Nonlinear functional regression by functional deep neural network with kernel embedding

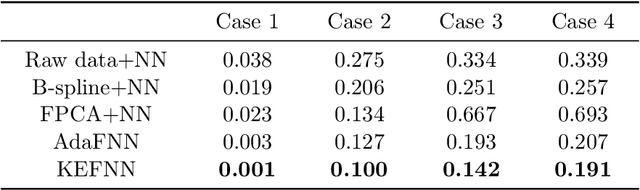
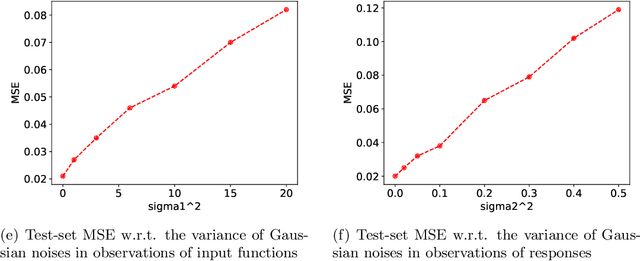
With the rapid development of deep learning in various fields of science and technology, such as speech recognition, image classification, and natural language processing, recently it is also widely applied in the functional data analysis (FDA) with some empirical success. However, due to the infinite dimensional input, we need a powerful dimension reduction method for functional learning tasks, especially for the nonlinear functional regression. In this paper, based on the idea of smooth kernel integral transformation, we propose a functional deep neural network with an efficient and fully data-dependent dimension reduction method. The architecture of our functional net consists of a kernel embedding step: an integral transformation with a data-dependent smooth kernel; a projection step: a dimension reduction by projection with eigenfunction basis based on the embedding kernel; and finally an expressive deep ReLU neural network for the prediction. The utilization of smooth kernel embedding enables our functional net to be discretization invariant, efficient, and robust to noisy observations, capable of utilizing information in both input functions and responses data, and have a low requirement on the number of discrete points for an unimpaired generalization performance. We conduct theoretical analysis including approximation error and generalization error analysis, and numerical simulations to verify these advantages of our functional net.