Convergence Analysis for Deep Sparse Coding via Convolutional Neural Networks

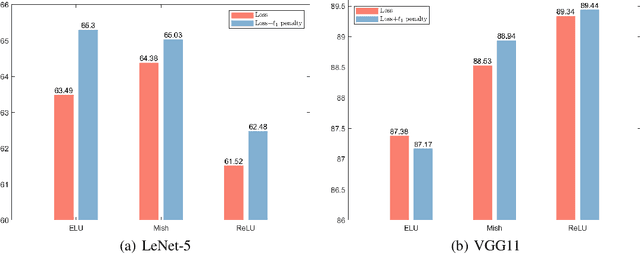
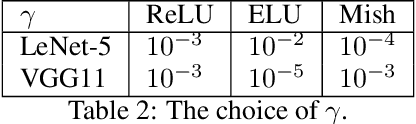
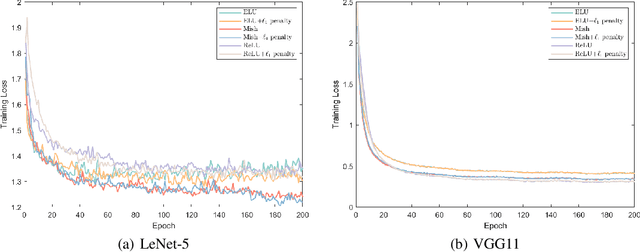
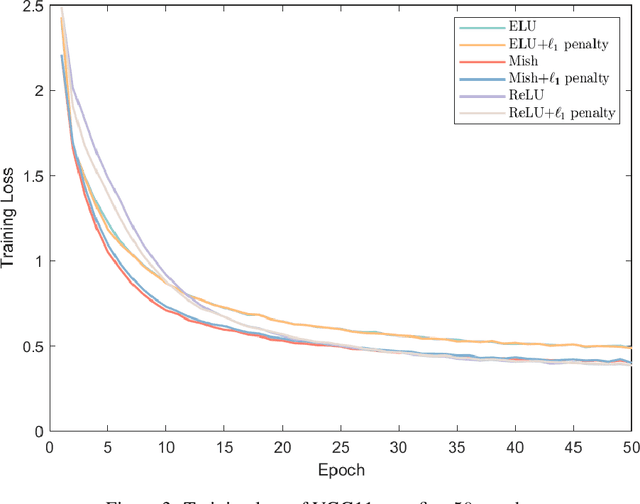
In this work, we explore the intersection of sparse coding theory and deep learning to enhance our understanding of feature extraction capabilities in advanced neural network architectures. We begin by introducing a novel class of Deep Sparse Coding (DSC) models and establish a thorough theoretical analysis of their uniqueness and stability properties. By applying iterative algorithms to these DSC models, we derive convergence rates for convolutional neural networks (CNNs) in their ability to extract sparse features. This provides a strong theoretical foundation for the use of CNNs in sparse feature learning tasks. We additionally extend this convergence analysis to more general neural network architectures, including those with diverse activation functions, as well as self-attention and transformer-based models. This broadens the applicability of our findings to a wide range of deep learning methods for deep sparse feature extraction. Inspired by the strong connection between sparse coding and CNNs, we also explore training strategies to encourage neural networks to learn more sparse features. Through numerical experiments, we demonstrate the effectiveness of these approaches, providing valuable insights for the design of efficient and interpretable deep learning models.

Bridging Smoothness and Approximation: Theoretical Insights into Over-Smoothing in Graph Neural Networks

In this paper, we explore the approximation theory of functions defined on graphs. Our study builds upon the approximation results derived from the $K$-functional. We establish a theoretical framework to assess the lower bounds of approximation for target functions using Graph Convolutional Networks (GCNs) and examine the over-smoothing phenomenon commonly observed in these networks. Initially, we introduce the concept of a $K$-functional on graphs, establishing its equivalence to the modulus of smoothness. We then analyze a typical type of GCN to demonstrate how the high-frequency energy of the output decays, an indicator of over-smoothing. This analysis provides theoretical insights into the nature of over-smoothing within GCNs. Furthermore, we establish a lower bound for the approximation of target functions by GCNs, which is governed by the modulus of smoothness of these functions. This finding offers a new perspective on the approximation capabilities of GCNs. In our numerical experiments, we analyze several widely applied GCNs and observe the phenomenon of energy decay. These observations corroborate our theoretical results on exponential decay order.

Permutation Equivariant Graph Framelets for Heterophilous Graph Learning

The nature of heterophilous graphs is significantly different with that of homophilous graphs, which causes difficulties in early graph neural network models and suggests aggregations beyond 1-hop neighborhood. In this paper, we develop a new way to implement multi-scale extraction via constructing Haar-type graph framelets with desired properties of permutation equivariance, efficiency, and sparsity, for deep learning tasks on graphs. We further design a graph framelet neural network model PEGFAN (Permutation Equivariant Graph Framelet Augmented Network) based on our constructed graph framelets. The experiments are conducted on a synthetic dataset and 9 benchmark datasets to compare performance with other state-of-the-art models. The result shows that our model can achieve best performance on certain datasets of heterophilous graphs (including the majority of heterophilous datasets with relatively larger sizes and denser connections) and competitive performance on the remaining.

A new activation for neural networks and its approximation

Deep learning with deep neural networks (DNNs) has attracted tremendous attention from various fields of science and technology recently. Activation functions for a DNN define the output of a neuron given an input or set of inputs. They are essential and inevitable in learning non-linear transformations and performing diverse computations among successive neuron layers. Thus, the design of activation functions is still an important topic in deep learning research. Meanwhile, theoretical studies on the approximation ability of DNNs with activation functions have been investigated within the last few years. In this paper, we propose a new activation function, named as "DLU", and investigate its approximation ability for functions with various smoothness and structures. Our theoretical results show that DLU networks can process competitive approximation performance with rational and ReLU networks, and have some advantages. Numerical experiments are conducted comparing DLU with the existing activations-ReLU, Leaky ReLU, and ELU, which illustrate the good practical performance of DLU.

Approximation analysis of CNNs from feature extraction view

Deep learning based on deep neural networks has been very successful in many practical applications, but it lacks enough theoretical understanding due to the network architectures and structures. In this paper, we establish the analysis for linear feature extraction by deep multi-channel convolutional neural networks(CNNs), which demonstrates the power of deep learning over traditional linear transformations, like Fourier, Wavelets, and Redundant dictionary coding methods. Moreover, we give an exact construction presenting how linear features extraction can be conducted efficiently with multi-channel CNNs. It can be applied to lower the essential dimension for approximating a high-dimensional function. Rates of function approximation by such deep networks implemented with channels and followed by fully-connected layers are investigated as well. Harmonic analysis for factorizing linear features into multi-resolution convolutions plays an essential role in our work. Nevertheless, a dedicate vectorization of matrices is constructed, which bridges 1D CNN and 2D CNN and allows us have corresponding 2D analysis.

Spherical Image Inpainting with Frame Transformation and Data-driven Prior Deep Networks

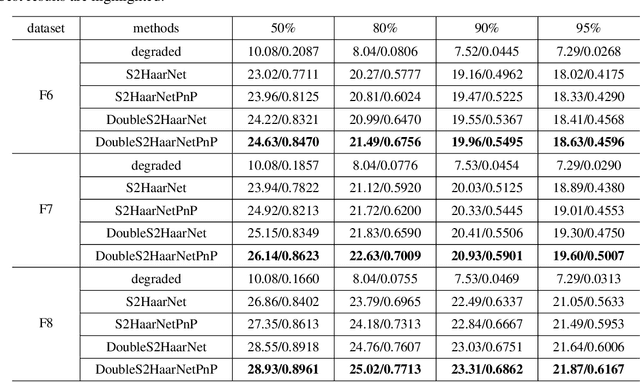
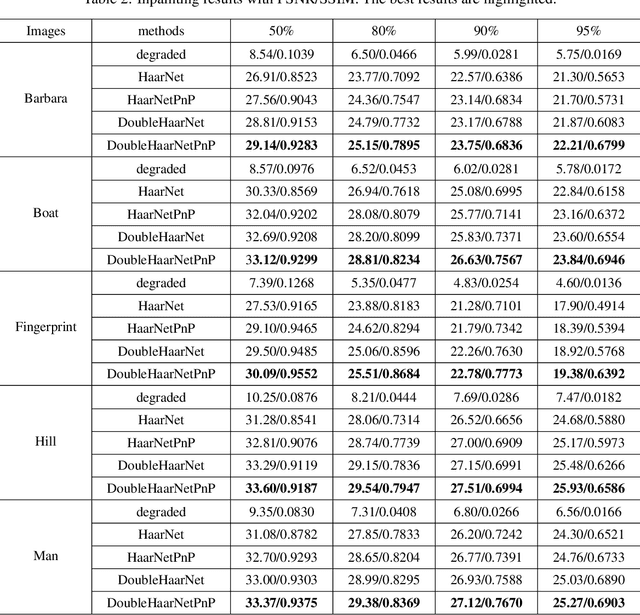
Spherical image processing has been widely applied in many important fields, such as omnidirectional vision for autonomous cars, global climate modelling, and medical imaging. It is non-trivial to extend an algorithm developed for flat images to the spherical ones. In this work, we focus on the challenging task of spherical image inpainting with deep learning-based regularizer. Instead of a naive application of existing models for planar images, we employ a fast directional spherical Haar framelet transform and develop a novel optimization framework based on a sparsity assumption of the framelet transform. Furthermore, by employing progressive encoder-decoder architecture, a new and better-performed deep CNN denoiser is carefully designed and works as an implicit regularizer. Finally, we use a plug-and-play method to handle the proposed optimization model, which can be implemented efficiently by training the CNN denoiser prior. Numerical experiments are conducted and show that the proposed algorithms can greatly recover damaged spherical images and achieve the best performance over purely using deep learning denoiser and plug-and-play model.

Convolutional Neural Networks for Spherical Signal Processing via Spherical Haar Tight Framelets

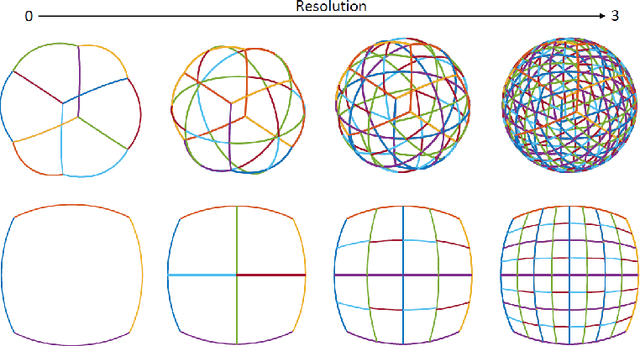
In this paper, we develop a general theoretical framework for constructing Haar-type tight framelets on any compact set with a hierarchical partition. In particular, we construct a novel area-regular hierarchical partition on the 2-sphere and establish its corresponding spherical Haar tight framelets with directionality. We conclude by evaluating and illustrating the effectiveness of our area-regular spherical Haar tight framelets in several denoising experiments. Furthermore, we propose a convolutional neural network (CNN) model for spherical signal denoising which employs the fast framelet decomposition and reconstruction algorithms. Experiment results show that our proposed CNN model outperforms threshold methods, and processes strong generalization and robustness properties.