Seedance 1.5 pro: A Native Audio-Visual Joint Generation Foundation Model

Recent strides in video generation have paved the way for unified audio-visual generation. In this work, we present Seedance 1.5 pro, a foundational model engineered specifically for native, joint audio-video generation. Leveraging a dual-branch Diffusion Transformer architecture, the model integrates a cross-modal joint module with a specialized multi-stage data pipeline, achieving exceptional audio-visual synchronization and superior generation quality. To ensure practical utility, we implement meticulous post-training optimizations, including Supervised Fine-Tuning (SFT) on high-quality datasets and Reinforcement Learning from Human Feedback (RLHF) with multi-dimensional reward models. Furthermore, we introduce an acceleration framework that boosts inference speed by over 10X. Seedance 1.5 pro distinguishes itself through precise multilingual and dialect lip-syncing, dynamic cinematic camera control, and enhanced narrative coherence, positioning it as a robust engine for professional-grade content creation. Seedance 1.5 pro is now accessible on Volcano Engine at https://console.volcengine.com/ark/region:ark+cn-beijing/experience/vision?type=GenVideo.

Soul: Breathe Life into Digital Human for High-fidelity Long-term Multimodal Animation

We propose a multimodal-driven framework for high-fidelity long-term digital human animation termed $\textbf{Soul}$, which generates semantically coherent videos from a single-frame portrait image, text prompts, and audio, achieving precise lip synchronization, vivid facial expressions, and robust identity preservation. We construct Soul-1M, containing 1 million finely annotated samples with a precise automated annotation pipeline (covering portrait, upper-body, full-body, and multi-person scenes) to mitigate data scarcity, and we carefully curate Soul-Bench for comprehensive and fair evaluation of audio-/text-guided animation methods. The model is built on the Wan2.2-5B backbone, integrating audio-injection layers and multiple training strategies together with threshold-aware codebook replacement to ensure long-term generation consistency. Meanwhile, step/CFG distillation and a lightweight VAE are used to optimize inference efficiency, achieving an 11.4$\times$ speedup with negligible quality loss. Extensive experiments show that Soul significantly outperforms current leading open-source and commercial models on video quality, video-text alignment, identity preservation, and lip-synchronization accuracy, demonstrating broad applicability in real-world scenarios such as virtual anchors and film production. Project page at https://zhangzjn.github.io/projects/Soul/

HOPS: High-order Polynomials with Self-supervised Dimension Reduction for Load Forecasting

Load forecasting is a fundamental task in smart grid. Many techniques have been applied to developing load forecasting models. Due to the challenges such as the Curse of Dimensionality, overfitting, and limited computing resources, multivariate higher-order polynomial models have received limited attention in load forecasting, despite their desirable mathematical foundations and optimization properties. In this paper, we propose low rank approximation and self-supervised dimension reduction to address the aforementioned issues. To further improve computational efficiency, we also introduce a fast Conjugate Gradient based algorithm for the proposed polynomial models. Based on the ISO New England dataset used in Global Energy Forecasting Competition 2017, the proposed method high-order polynomials with self-supervised dimension reduction (HOPS) demonstrates higher forecasting accuracy over several competitive models. Additionally, experimental results indicate that our approach alleviates redundant variable construction, achieving better forecasts with fewer input variables.

Deeper Insights into Deep Graph Convolutional Networks: Stability and Generalization

Graph convolutional networks (GCNs) have emerged as powerful models for graph learning tasks, exhibiting promising performance in various domains. While their empirical success is evident, there is a growing need to understand their essential ability from a theoretical perspective. Existing theoretical research has primarily focused on the analysis of single-layer GCNs, while a comprehensive theoretical exploration of the stability and generalization of deep GCNs remains limited. In this paper, we bridge this gap by delving into the stability and generalization properties of deep GCNs, aiming to provide valuable insights by characterizing rigorously the associated upper bounds. Our theoretical results reveal that the stability and generalization of deep GCNs are influenced by certain key factors, such as the maximum absolute eigenvalue of the graph filter operators and the depth of the network. Our theoretical studies contribute to a deeper understanding of the stability and generalization properties of deep GCNs, potentially paving the way for developing more reliable and well-performing models.

Spherical Analysis of Learning Nonlinear Functionals

In recent years, there has been growing interest in the field of functional neural networks. They have been proposed and studied with the aim of approximating continuous functionals defined on sets of functions on Euclidean domains. In this paper, we consider functionals defined on sets of functions on spheres. The approximation ability of deep ReLU neural networks is investigated by novel spherical analysis using an encoder-decoder framework. An encoder comes up first to accommodate the infinite-dimensional nature of the domain of functionals. It utilizes spherical harmonics to help us extract the latent finite-dimensional information of functions, which in turn facilitates in the next step of approximation analysis using fully connected neural networks. Moreover, real-world objects are frequently sampled discretely and are often corrupted by noise. Therefore, encoders with discrete input and those with discrete and random noise input are constructed, respectively. The approximation rates with different encoder structures are provided therein.

Convergence Analysis for Deep Sparse Coding via Convolutional Neural Networks

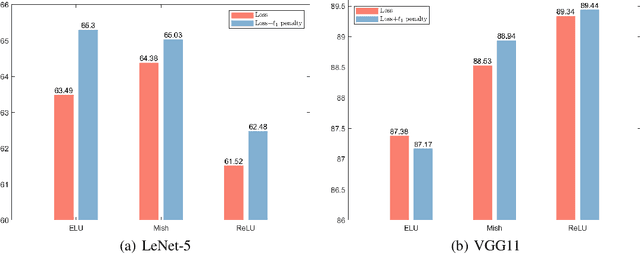
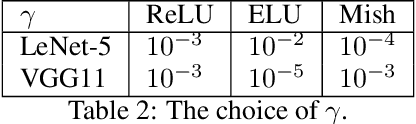
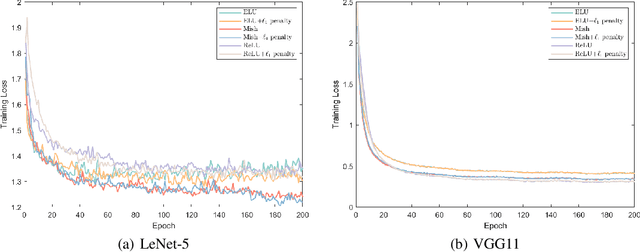
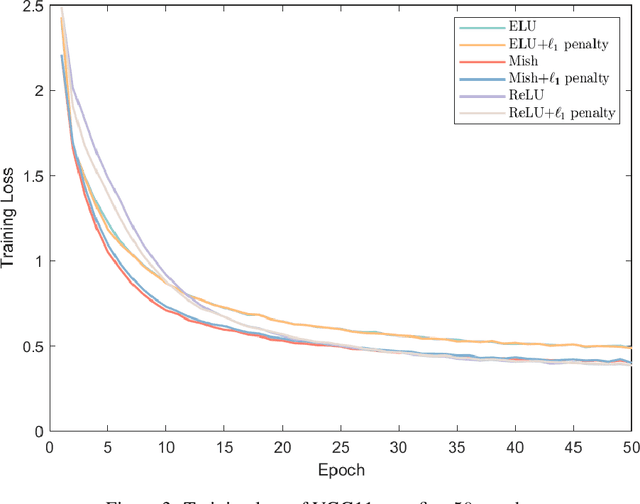
In this work, we explore the intersection of sparse coding theory and deep learning to enhance our understanding of feature extraction capabilities in advanced neural network architectures. We begin by introducing a novel class of Deep Sparse Coding (DSC) models and establish a thorough theoretical analysis of their uniqueness and stability properties. By applying iterative algorithms to these DSC models, we derive convergence rates for convolutional neural networks (CNNs) in their ability to extract sparse features. This provides a strong theoretical foundation for the use of CNNs in sparse feature learning tasks. We additionally extend this convergence analysis to more general neural network architectures, including those with diverse activation functions, as well as self-attention and transformer-based models. This broadens the applicability of our findings to a wide range of deep learning methods for deep sparse feature extraction. Inspired by the strong connection between sparse coding and CNNs, we also explore training strategies to encourage neural networks to learn more sparse features. Through numerical experiments, we demonstrate the effectiveness of these approaches, providing valuable insights for the design of efficient and interpretable deep learning models.

Theoretical Insights into CycleGAN: Analyzing Approximation and Estimation Errors in Unpaired Data Generation

In this paper, we focus on analyzing the excess risk of the unpaired data generation model, called CycleGAN. Unlike classical GANs, CycleGAN not only transforms data between two unpaired distributions but also ensures the mappings are consistent, which is encouraged by the cycle-consistency term unique to CycleGAN. The increasing complexity of model structure and the addition of the cycle-consistency term in CycleGAN present new challenges for error analysis. By considering the impact of both the model architecture and training procedure, the risk is decomposed into two terms: approximation error and estimation error. These two error terms are analyzed separately and ultimately combined by considering the trade-off between them. Each component is rigorously analyzed; the approximation error through constructing approximations of the optimal transport maps, and the estimation error through establishing an upper bound using Rademacher complexity. Our analysis not only isolates these errors but also explores the trade-offs between them, which provides a theoretical insights of how CycleGAN's architecture and training procedures influence its performance.

Bridging Smoothness and Approximation: Theoretical Insights into Over-Smoothing in Graph Neural Networks

In this paper, we explore the approximation theory of functions defined on graphs. Our study builds upon the approximation results derived from the $K$-functional. We establish a theoretical framework to assess the lower bounds of approximation for target functions using Graph Convolutional Networks (GCNs) and examine the over-smoothing phenomenon commonly observed in these networks. Initially, we introduce the concept of a $K$-functional on graphs, establishing its equivalence to the modulus of smoothness. We then analyze a typical type of GCN to demonstrate how the high-frequency energy of the output decays, an indicator of over-smoothing. This analysis provides theoretical insights into the nature of over-smoothing within GCNs. Furthermore, we establish a lower bound for the approximation of target functions by GCNs, which is governed by the modulus of smoothness of these functions. This finding offers a new perspective on the approximation capabilities of GCNs. In our numerical experiments, we analyze several widely applied GCNs and observe the phenomenon of energy decay. These observations corroborate our theoretical results on exponential decay order.

Stratified Avatar Generation from Sparse Observations

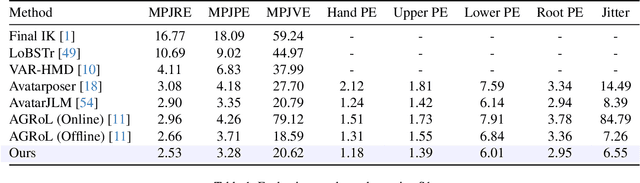
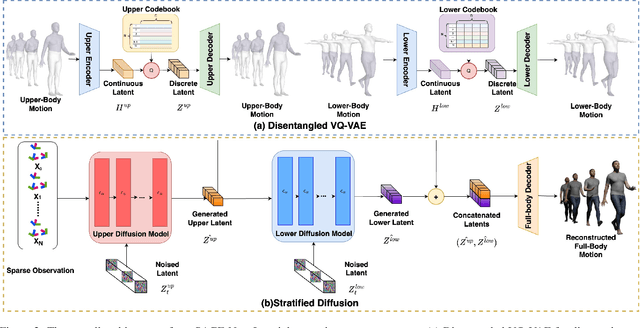
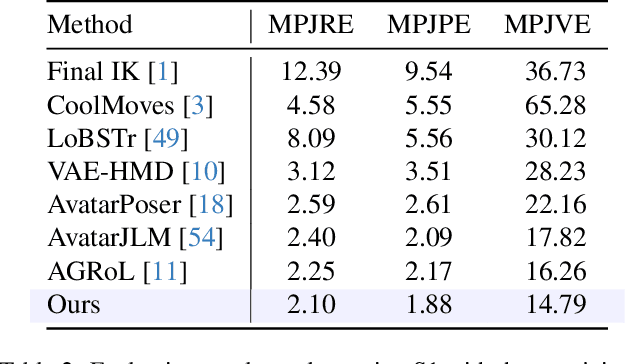
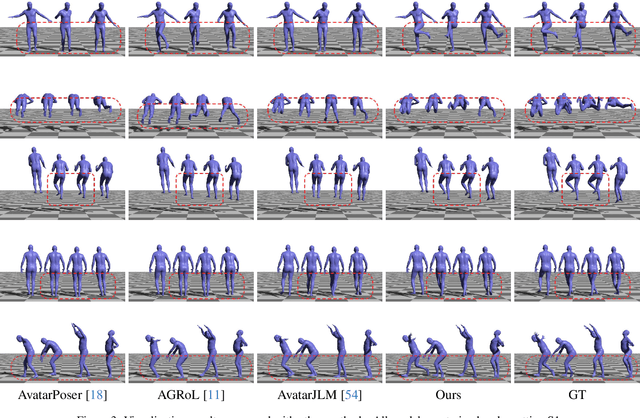
Estimating 3D full-body avatars from AR/VR devices is essential for creating immersive experiences in AR/VR applications. This task is challenging due to the limited input from Head Mounted Devices, which capture only sparse observations from the head and hands. Predicting the full-body avatars, particularly the lower body, from these sparse observations presents significant difficulties. In this paper, we are inspired by the inherent property of the kinematic tree defined in the Skinned Multi-Person Linear (SMPL) model, where the upper body and lower body share only one common ancestor node, bringing the potential of decoupled reconstruction. We propose a stratified approach to decouple the conventional full-body avatar reconstruction pipeline into two stages, with the reconstruction of the upper body first and a subsequent reconstruction of the lower body conditioned on the previous stage. To implement this straightforward idea, we leverage the latent diffusion model as a powerful probabilistic generator, and train it to follow the latent distribution of decoupled motions explored by a VQ-VAE encoder-decoder model. Extensive experiments on AMASS mocap dataset demonstrate our state-of-the-art performance in the reconstruction of full-body motions.

On the rates of convergence for learning with convolutional neural networks

We study approximation and learning capacities of convolutional neural networks (CNNs) with one-side zero-padding and multiple channels. Our first result proves a new approximation bound for CNNs with certain constraint on the weights. Our second result gives new analysis on the covering number of feed-forward neural networks with CNNs as special cases. The analysis carefully takes into account the size of the weights and hence gives better bounds than the existing literature in some situations. Using these two results, we are able to derive rates of convergence for estimators based on CNNs in many learning problems. In particular, we establish minimax optimal convergence rates of the least squares based on CNNs for learning smooth functions in the nonparametric regression setting. For binary classification, we derive convergence rates for CNN classifiers with hinge loss and logistic loss. It is also shown that the obtained rates for classification are minimax optimal in some common settings.