Deeper Insights into Deep Graph Convolutional Networks: Stability and Generalization

Graph convolutional networks (GCNs) have emerged as powerful models for graph learning tasks, exhibiting promising performance in various domains. While their empirical success is evident, there is a growing need to understand their essential ability from a theoretical perspective. Existing theoretical research has primarily focused on the analysis of single-layer GCNs, while a comprehensive theoretical exploration of the stability and generalization of deep GCNs remains limited. In this paper, we bridge this gap by delving into the stability and generalization properties of deep GCNs, aiming to provide valuable insights by characterizing rigorously the associated upper bounds. Our theoretical results reveal that the stability and generalization of deep GCNs are influenced by certain key factors, such as the maximum absolute eigenvalue of the graph filter operators and the depth of the network. Our theoretical studies contribute to a deeper understanding of the stability and generalization properties of deep GCNs, potentially paving the way for developing more reliable and well-performing models.

Subgraph-based Tight Frames on Graphs with Compact Supports and Vanishing Moments

In this work, we proposed a novel and general method to construct tight frames on graphs with compact supports based on a series of hierarchical partitions. Starting from our abstract construction that generalizes previous methods based on partition trees, we are able to flexibly incorporate subgraph Laplacians into our design of graph frames. Consequently, our general methods permit adjusting the (subgraph) vanishing moments of the framelets and extra properties, such as directionality, for efficiently representing graph signals with path-like supports. Several variants are explicitly defined and tested. Experimental results show our proposed graph frames perform superiorly in non-linear approximation tasks.

Permutation Equivariant Graph Framelets for Heterophilous Graph Learning

The nature of heterophilous graphs is significantly different with that of homophilous graphs, which causes difficulties in early graph neural network models and suggests aggregations beyond 1-hop neighborhood. In this paper, we develop a new way to implement multi-scale extraction via constructing Haar-type graph framelets with desired properties of permutation equivariance, efficiency, and sparsity, for deep learning tasks on graphs. We further design a graph framelet neural network model PEGFAN (Permutation Equivariant Graph Framelet Augmented Network) based on our constructed graph framelets. The experiments are conducted on a synthetic dataset and 9 benchmark datasets to compare performance with other state-of-the-art models. The result shows that our model can achieve best performance on certain datasets of heterophilous graphs (including the majority of heterophilous datasets with relatively larger sizes and denser connections) and competitive performance on the remaining.

Convolutional Neural Networks for Spherical Signal Processing via Spherical Haar Tight Framelets

In this paper, we develop a general theoretical framework for constructing Haar-type tight framelets on any compact set with a hierarchical partition. In particular, we construct a novel area-regular hierarchical partition on the 2-sphere and establish its corresponding spherical Haar tight framelets with directionality. We conclude by evaluating and illustrating the effectiveness of our area-regular spherical Haar tight framelets in several denoising experiments. Furthermore, we propose a convolutional neural network (CNN) model for spherical signal denoising which employs the fast framelet decomposition and reconstruction algorithms. Experiment results show that our proposed CNN model outperforms threshold methods, and processes strong generalization and robustness properties.

Decimated Framelet System on Graphs and Fast G-Framelet Transforms

Graph representation learning has many real-world applications, from super-resolution imaging, 3D computer vision to drug repurposing, protein classification, social networks analysis. An adequate representation of graph data is vital to the learning performance of a statistical or machine learning model for graph-structured data. In this paper, we propose a novel multiscale representation system for graph data, called decimated framelets, which form a localized tight frame on the graph. The decimated framelet system allows storage of the graph data representation on a coarse-grained chain and processes the graph data at multi scales where at each scale, the data is stored at a subgraph. Based on this, we then establish decimated G-framelet transforms for the decomposition and reconstruction of the graph data at multi resolutions via a constructive data-driven filter bank. The graph framelets are built on a chain-based orthonormal basis that supports fast graph Fourier transforms. From this, we give a fast algorithm for the decimated G-framelet transforms, or FGT, that has linear computational complexity O(N) for a graph of size N. The theory of decimated framelets and FGT is verified with numerical examples for random graphs. The effectiveness is demonstrated by real-world applications, including multiresolution analysis for traffic network, and graph neural networks for graph classification tasks.

Adaptive directional Haar tight framelets on bounded domains for digraph signal representations

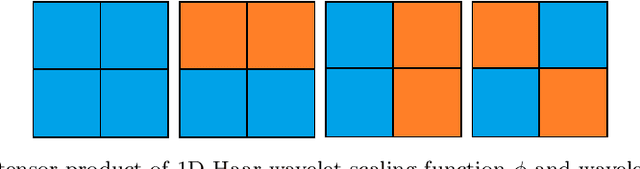
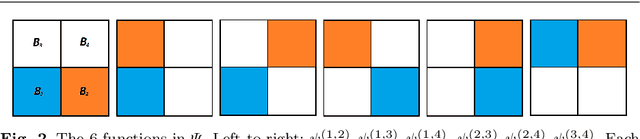
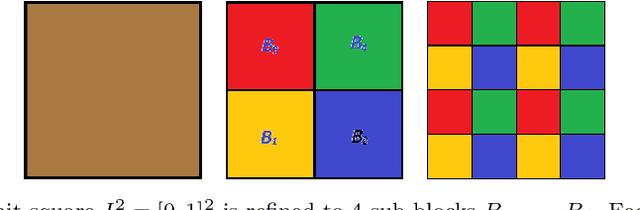
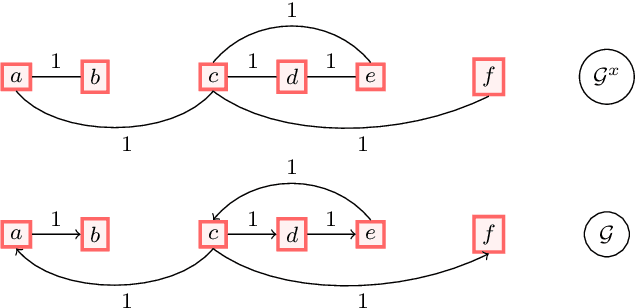
Based on hierarchical partitions, we provide the construction of Haar-type tight framelets on any compact set $K\subseteq \mathbb{R}^d$. In particular, on the unit block $[0,1]^d$, such tight framelets can be built to be with adaptivity and directionality. We show that the adaptive directional Haar tight framelet systems can be used for digraph signal representations. Some examples are provided to illustrate results in this paper.

HaarPooling: Graph Pooling with Compressive Haar Basis

Deep Graph Neural Networks (GNNs) are instrumental in graph classification and graph-based regression tasks. In these tasks, graph pooling is a critical ingredient by which GNNs adapt to input graphs of varying size and structure. We propose a new graph pooling operation based on compressive Haar transforms, called HaarPooling. HaarPooling is computed following a chain of sequential clusterings of the input graph. The input of each pooling layer is transformed by the compressive Haar basis of the corresponding clustering. HaarPooling operates in the frequency domain by the synthesis of nodes in the same cluster and filters out fine detail information by compressive Haar transforms. Such transforms provide an effective characterization of the data and preserve the structure information of the input graph. By the sparsity of the Haar basis, the computation of HaarPooling is of linear complexity. The GNN with HaarPooling and existing graph convolution layers achieves state-of-the-art performance on diverse graph classification problems.

Fast Haar Transforms for Graph Neural Networks

Graph Neural Networks (GNNs) have become a topic of intense research recently due to their powerful capability in high-dimensional classification and regression tasks for graph-structured data. However, as GNNs typically define the graph convolution by the orthonormal basis for the graph Laplacian, they suffer from high computational cost when the graph size is large. This paper introduces the Haar basis, a sparse and localized orthonormal system for graph, constructed from a coarse-grained chain on the graph. The graph convolution under Haar basis --- the Haar convolution can be defined accordingly for GNNs. The sparsity and locality of the Haar basis allow Fast Haar Transforms (FHTs) on graph, by which a fast evaluation of Haar convolution between the graph signals and the filters can be achieved. We conduct preliminary experiments on GNNs equipped with Haar convolution, which can obtain state-of-the-art results for a variety of geometric deep learning tasks.