Supermodular Rank: Set Function Decomposition and Optimization

We define the supermodular rank of a function on a lattice. This is the smallest number of terms needed to decompose it into a sum of supermodular functions. The supermodular summands are defined with respect to different partial orders. We characterize the maximum possible value of the supermodular rank and describe the functions with fixed supermodular rank. We analogously define the submodular rank. We use submodular decompositions to optimize set functions. Given a bound on the submodular rank of a set function, we formulate an algorithm that splits an optimization problem into submodular subproblems. We show that this method improves the approximation ratio guarantees of several algorithms for monotone set function maximization and ratio of set functions minimization, at a computation overhead that depends on the submodular rank.

Characterizing the Spectrum of the NTK via a Power Series Expansion

Under mild conditions on the network initialization we derive a power series expansion for the Neural Tangent Kernel (NTK) of arbitrarily deep feedforward networks in the infinite width limit. We provide expressions for the coefficients of this power series which depend on both the Hermite coefficients of the activation function as well as the depth of the network. We observe faster decay of the Hermite coefficients leads to faster decay in the NTK coefficients. Using this series, first we relate the effective rank of the NTK to the effective rank of the input-data Gram. Second, for data drawn uniformly on the sphere we derive an explicit formula for the eigenvalues of the NTK, which shows faster decay in the NTK coefficients implies a faster decay in its spectrum. From this we recover existing results on eigenvalue asymptotics for ReLU networks and comment on how the activation function influences the RKHS. Finally, for generic data and activation functions with sufficiently fast Hermite coefficient decay, we derive an asymptotic upper bound on the spectrum of the NTK.

Spectral Bias Outside the Training Set for Deep Networks in the Kernel Regime

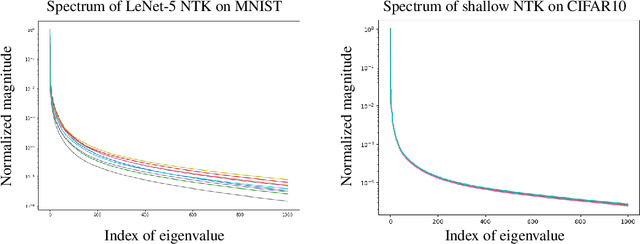
We provide quantitative bounds measuring the $L^2$ difference in function space between the trajectory of a finite-width network trained on finitely many samples from the idealized kernel dynamics of infinite width and infinite data. An implication of the bounds is that the network is biased to learn the top eigenfunctions of the Neural Tangent Kernel not just on the training set but over the entire input space. This bias depends on the model architecture and input distribution alone and thus does not depend on the target function which does not need to be in the RKHS of the kernel. The result is valid for deep architectures with fully connected, convolutional, and residual layers. Furthermore the width does not need to grow polynomially with the number of samples in order to obtain high probability bounds up to a stopping time. The proof exploits the low-effective-rank property of the Fisher Information Matrix at initialization, which implies a low effective dimension of the model (far smaller than the number of parameters). We conclude that local capacity control from the low effective rank of the Fisher Information Matrix is still underexplored theoretically.

Implicit Bias of MSE Gradient Optimization in Underparameterized Neural Networks

We study the dynamics of a neural network in function space when optimizing the mean squared error via gradient flow. We show that in the underparameterized regime the network learns eigenfunctions of an integral operator $T_{K^\infty}$ determined by the Neural Tangent Kernel (NTK) at rates corresponding to their eigenvalues. For example, for uniformly distributed data on the sphere $S^{d - 1}$ and rotation invariant weight distributions, the eigenfunctions of $T_{K^\infty}$ are the spherical harmonics. Our results can be understood as describing a spectral bias in the underparameterized regime. The proofs use the concept of "Damped Deviations", where deviations of the NTK matter less for eigendirections with large eigenvalues due to the occurence of a damping factor. Aside from the underparameterized regime, the damped deviations point-of-view can be used to track the dynamics of the empirical risk in the overparameterized setting, allowing us to extend certain results in the literature. We conclude that damped deviations offers a simple and unifying perspective of the dynamics when optimizing the squared error.

How Framelets Enhance Graph Neural Networks

This paper presents a new approach for assembling graph neural networks based on framelet transforms. The latter provides a multi-scale representation for graph-structured data. With the framelet system, we can decompose the graph feature into low-pass and high-pass frequencies as extracted features for network training, which then defines a framelet-based graph convolution. The framelet decomposition naturally induces a graph pooling strategy by aggregating the graph feature into low-pass and high-pass spectra, which considers both the feature values and geometry of the graph data and conserves the total information. The graph neural networks with the proposed framelet convolution and pooling achieve state-of-the-art performance in many types of node and graph prediction tasks. Moreover, we propose shrinkage as a new activation for the framelet convolution, which thresholds the high-frequency information at different scales. Compared to ReLU, shrinkage in framelet convolution improves the graph neural network model in terms of denoising and signal compression: noises in both node and structure can be significantly reduced by accurately cutting off the high-pass coefficients from framelet decomposition, and the signal can be compressed to less than half its original size with the prediction performance well preserved.

Wasserstein Proximal of GANs

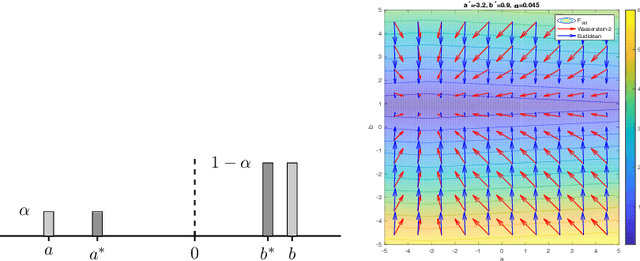
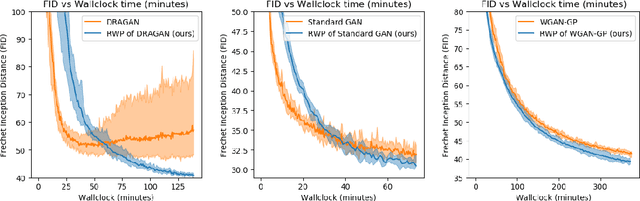
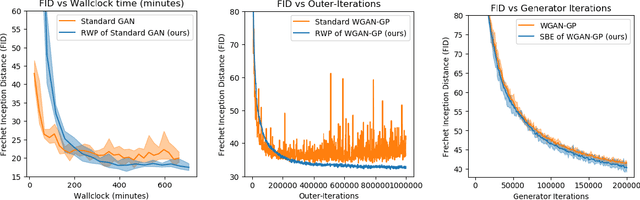
We introduce a new method for training generative adversarial networks by applying the Wasserstein-2 metric proximal on the generators. The approach is based on Wasserstein information geometry. It defines a parametrization invariant natural gradient by pulling back optimal transport structures from probability space to parameter space. We obtain easy-to-implement iterative regularizers for the parameter updates of implicit deep generative models. Our experiments demonstrate that this method improves the speed and stability of training in terms of wall-clock time and Fr\'echet Inception Distance.

Tight Bounds on the Smallest Eigenvalue of the Neural Tangent Kernel for Deep ReLU Networks

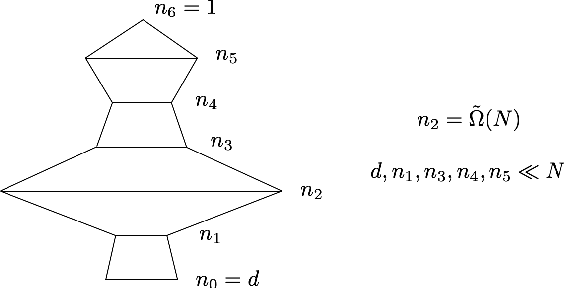
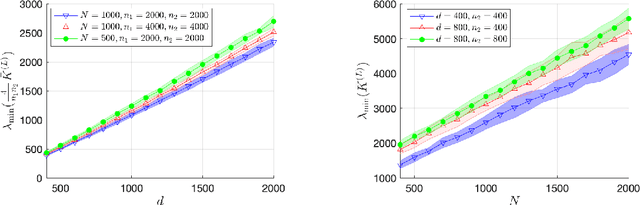
A recent line of work has analyzed the theoretical properties of deep neural networks via the Neural Tangent Kernel (NTK). In particular, the smallest eigenvalue of the NTK has been related to memorization capacity, convergence of gradient descent algorithms and generalization of deep nets. However, existing results either provide bounds in the two-layer setting or assume that the spectrum of the NTK is bounded away from 0 for multi-layer networks. In this paper, we provide tight bounds on the smallest eigenvalue of NTK matrices for deep ReLU networks, both in the limiting case of infinite widths and for finite widths. In the finite-width setting, the network architectures we consider are quite general: we require the existence of a wide layer with roughly order of $N$ neurons, $N$ being the number of data samples; and the scaling of the remaining widths is arbitrary (up to logarithmic factors). To obtain our results, we analyze various quantities of independent interest: we give lower bounds on the smallest singular value of feature matrices, and upper bounds on the Lipschitz constant of input-output feature maps.

Kernelized Wasserstein Natural Gradient

Many machine learning problems can be expressed as the optimization of some cost functional over a parametric family of probability distributions. It is often beneficial to solve such optimization problems using natural gradient methods. These methods are invariant to the parametrization of the family, and thus can yield more effective optimization. Unfortunately, computing the natural gradient is challenging as it requires inverting a high dimensional matrix at each iteration. We propose a general framework to approximate the natural gradient for the Wasserstein metric, by leveraging a dual formulation of the metric restricted to a Reproducing Kernel Hilbert Space. Our approach leads to an estimator for gradient direction that can trade-off accuracy and computational cost, with theoretical guarantees. We verify its accuracy on simple examples, and show the advantage of using such an estimator in classification tasks on Cifar10 and Cifar100 empirically.