Linear causal disentanglement via higher-order cumulants

Linear causal disentanglement is a recent method in causal representation learning to describe a collection of observed variables via latent variables with causal dependencies between them. It can be viewed as a generalization of both independent component analysis and linear structural equation models. We study the identifiability of linear causal disentanglement, assuming access to data under multiple contexts, each given by an intervention on a latent variable. We show that one perfect intervention on each latent variable is sufficient and in the worst case necessary to recover parameters under perfect interventions, generalizing previous work to allow more latent than observed variables. We give a constructive proof that computes parameters via a coupled tensor decomposition. For soft interventions, we find the equivalence class of latent graphs and parameters that are consistent with observed data, via the study of a system of polynomial equations. Our results hold assuming the existence of non-zero higher-order cumulants, which implies non-Gaussianity of variables.

Contrastive independent component analysis

Visualizing data and finding patterns in data are ubiquitous problems in the sciences. Increasingly, applications seek signal and structure in a contrastive setting: a foreground dataset relative to a background dataset. For this purpose, we propose contrastive independent component analysis (cICA). This generalizes independent component analysis to independent latent variables across a foreground and background. We propose a hierarchical tensor decomposition algorithm for cICA. We study the identifiability of cICA and demonstrate its performance visualizing data and finding patterns in data, using synthetic and real-world datasets, comparing the approach to existing contrastive methods.

Supermodular Rank: Set Function Decomposition and Optimization

We define the supermodular rank of a function on a lattice. This is the smallest number of terms needed to decompose it into a sum of supermodular functions. The supermodular summands are defined with respect to different partial orders. We characterize the maximum possible value of the supermodular rank and describe the functions with fixed supermodular rank. We analogously define the submodular rank. We use submodular decompositions to optimize set functions. Given a bound on the submodular rank of a set function, we formulate an algorithm that splits an optimization problem into submodular subproblems. We show that this method improves the approximation ratio guarantees of several algorithms for monotone set function maximization and ratio of set functions minimization, at a computation overhead that depends on the submodular rank.

Linear Causal Disentanglement via Interventions

Causal disentanglement seeks a representation of data involving latent variables that relate to one another via a causal model. A representation is identifiable if both the latent model and the transformation from latent to observed variables are unique. In this paper, we study observed variables that are a linear transformation of a linear latent causal model. Data from interventions are necessary for identifiability: if one latent variable is missing an intervention, we show that there exist distinct models that cannot be distinguished. Conversely, we show that a single intervention on each latent variable is sufficient for identifiability. Our proof uses a generalization of the RQ decomposition of a matrix that replaces the usual orthogonal and upper triangular conditions with analogues depending on a partial order on the rows of the matrix, with partial order determined by a latent causal model. We corroborate our theoretical results with a method for causal disentanglement that accurately recovers a latent causal model.

Learning Paths from Signature Tensors

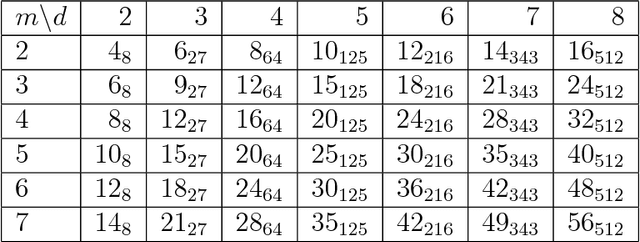
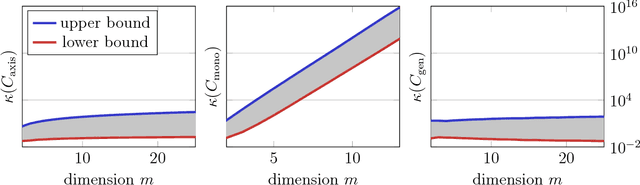
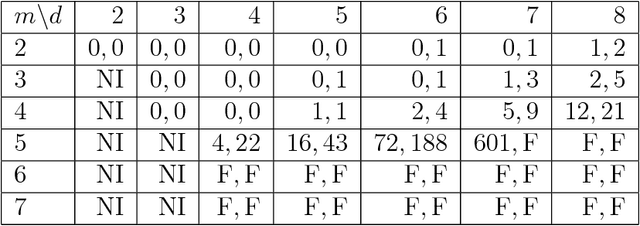
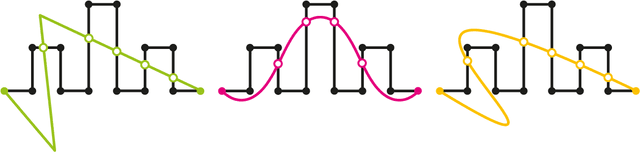
Matrix congruence extends naturally to the setting of tensors. We apply methods from tensor decomposition, algebraic geometry and numerical optimization to this group action. Given a tensor in the orbit of another tensor, we compute a matrix which transforms one to the other. Our primary application is an inverse problem from stochastic analysis: the recovery of paths from their signature tensors of order three. We establish identifiability results and recovery algorithms for piecewise linear paths, polynomial paths, and generic dictionaries. A detailed analysis of the relevant condition numbers is presented. We also compute the shortest path with a given signature tensor.

Duality of Graphical Models and Tensor Networks

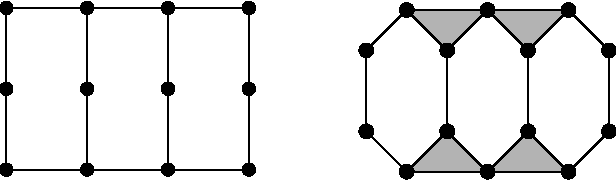
In this article we show the duality between tensor networks and undirected graphical models with discrete variables. We study tensor networks on hypergraphs, which we call tensor hypernetworks. We show that the tensor hypernetwork on a hypergraph exactly corresponds to the graphical model given by the dual hypergraph. We translate various notions under duality. For example, marginalization in a graphical model is dual to contraction in the tensor network. Algorithms also translate under duality. We show that belief propagation corresponds to a known algorithm for tensor network contraction. This article is a reminder that the research areas of graphical models and tensor networks can benefit from interaction.

Mixtures and products in two graphical models

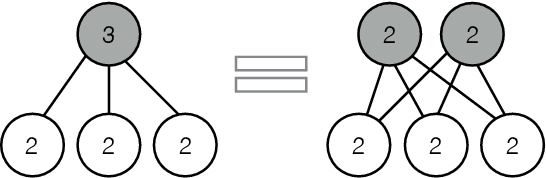
We compare two statistical models of three binary random variables. One is a mixture model and the other is a product of mixtures model called a restricted Boltzmann machine. Although the two models we study look different from their parametrizations, we show that they represent the same set of distributions on the interior of the probability simplex, and are equal up to closure. We give a semi-algebraic description of the model in terms of six binomial inequalities and obtain closed form expressions for the maximum likelihood estimates. We briefly discuss extensions to larger models.

Tensor clustering with algebraic constraints gives interpretable groups of crosstalk mechanisms in breast cancer

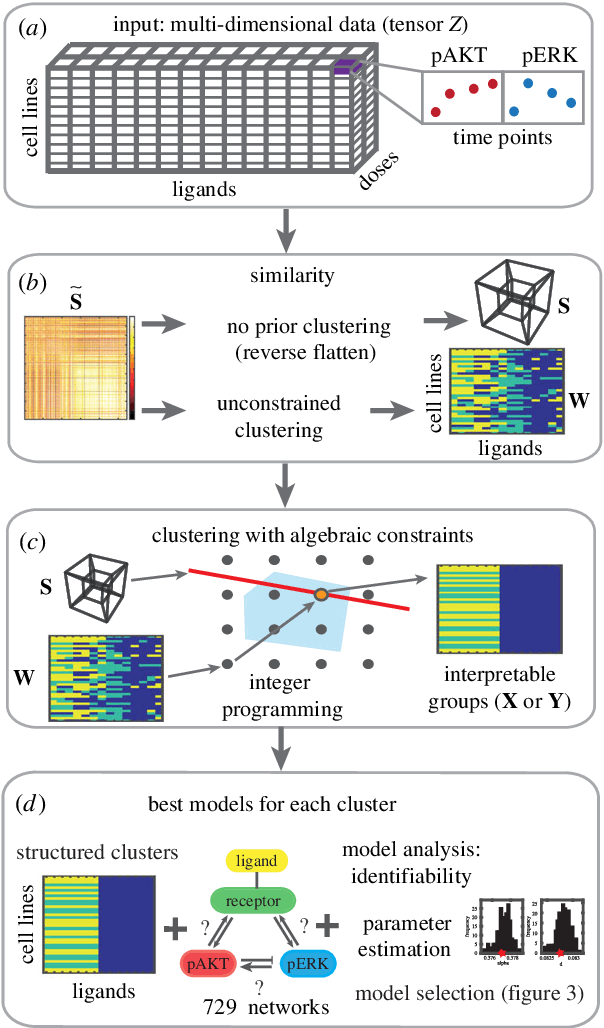
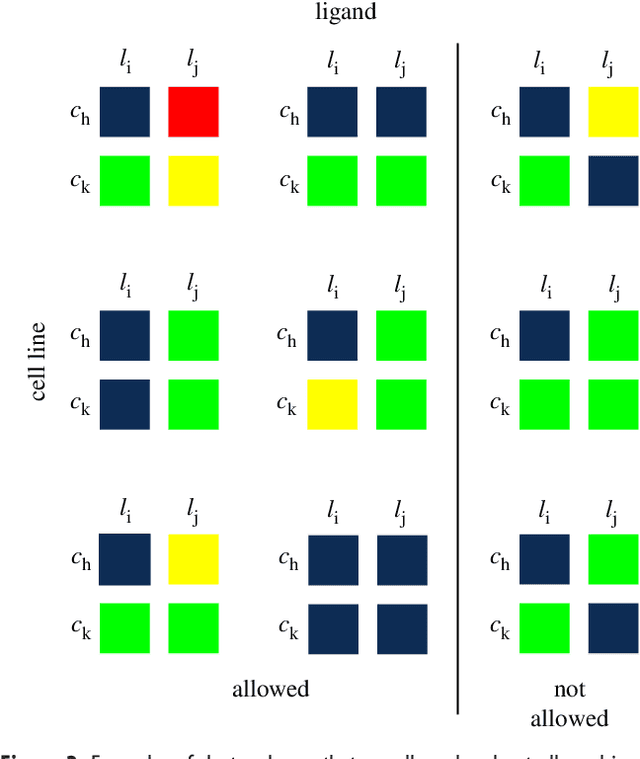
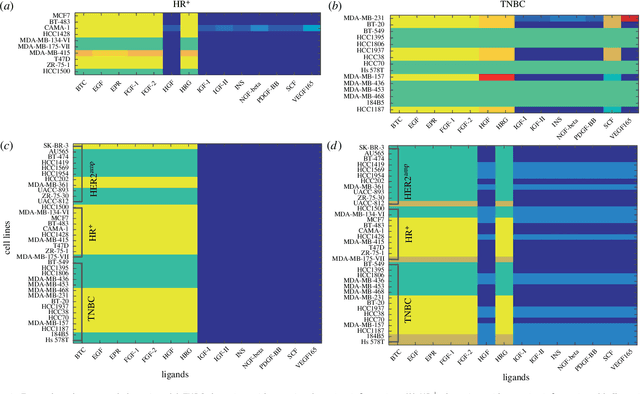
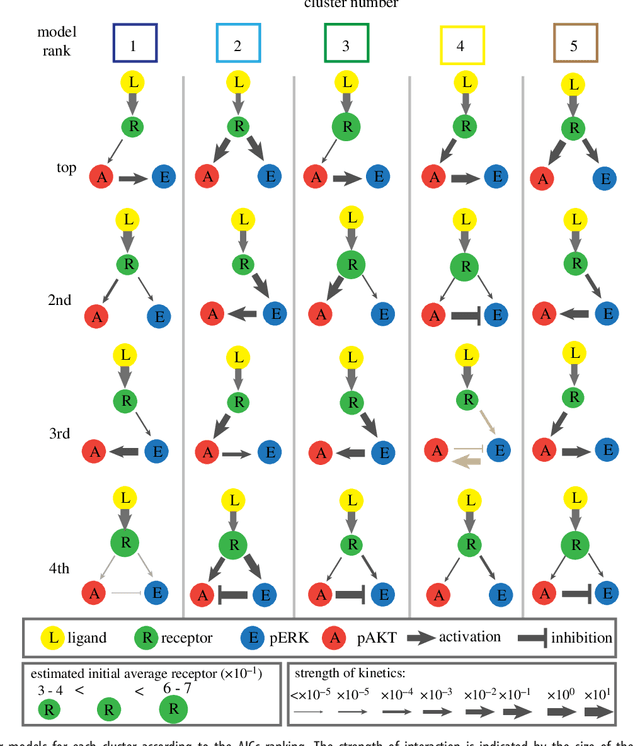
We introduce a tensor-based clustering method to extract sparse, low-dimensional structure from high-dimensional, multi-indexed datasets. Specifically, this framework is designed to enable detection of clusters of data in the presence of structural requirements which we encode as algebraic constraints in a linear program. We illustrate our method on a collection of experiments measuring the response of genetically diverse breast cancer cell lines to an array of ligands. Each experiment consists of a cell line-ligand combination, and contains time-course measurements of the early-signalling kinases MAPK and AKT at two different ligand dose levels. By imposing appropriate structural constraints and respecting the multi-indexed structure of the data, our clustering analysis can be optimized for biological interpretation and therapeutic understanding. We then perform a systematic, large-scale exploration of mechanistic models of MAPK-AKT crosstalk for each cluster. This analysis allows us to quantify the heterogeneity of breast cancer cell subtypes, and leads to hypotheses about the mechanisms by which cell lines respond to ligands. Our clustering method is general and can be tailored to a variety of applications in science and industry.