Mixtures and products in two graphical models
Paper and Code
Sep 15, 2017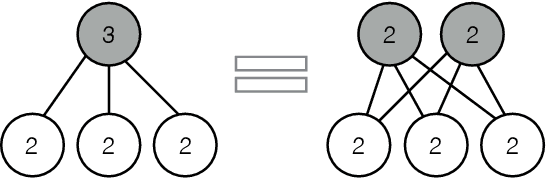
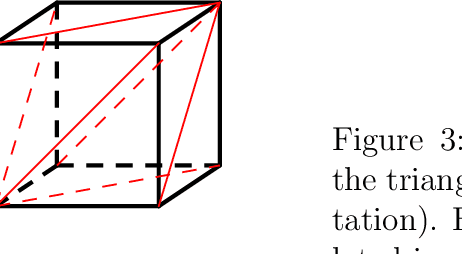
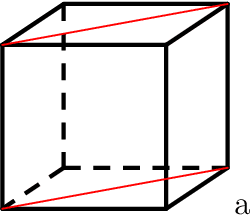
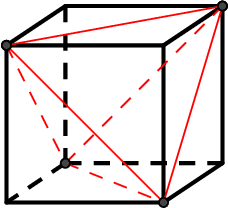
We compare two statistical models of three binary random variables. One is a mixture model and the other is a product of mixtures model called a restricted Boltzmann machine. Although the two models we study look different from their parametrizations, we show that they represent the same set of distributions on the interior of the probability simplex, and are equal up to closure. We give a semi-algebraic description of the model in terms of six binomial inequalities and obtain closed form expressions for the maximum likelihood estimates. We briefly discuss extensions to larger models.
* 18 pages, 7 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge