tPARAFAC2: Tracking evolving patterns in (incomplete) temporal data

Tensor factorizations have been widely used for the task of uncovering patterns in various domains. Often, the input is time-evolving, shifting the goal to tracking the evolution of underlying patterns instead. To adapt to this more complex setting, existing methods incorporate temporal regularization but they either have overly constrained structural requirements or lack uniqueness which is crucial for interpretation. In this paper, in order to capture the underlying evolving patterns, we introduce t(emporal)PARAFAC2 which utilizes temporal smoothness regularization on the evolving factors. We propose an algorithmic framework that employs Alternating Optimization (AO) and the Alternating Direction Method of Multipliers (ADMM) to fit the model. Furthermore, we extend the algorithmic framework to the case of partially observed data. Our numerical experiments on both simulated and real datasets demonstrate the effectiveness of the temporal smoothness regularization, in particular, in the case of data with missing entries. We also provide an extensive comparison of different approaches for handling missing data within the proposed framework.

A Time-aware tensor decomposition for tracking evolving patterns

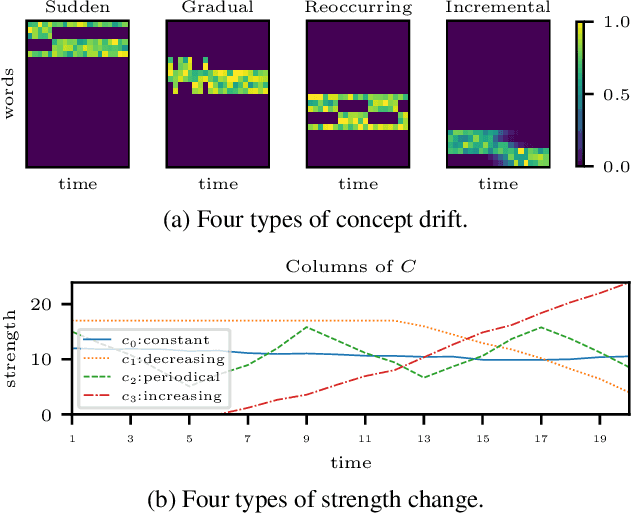
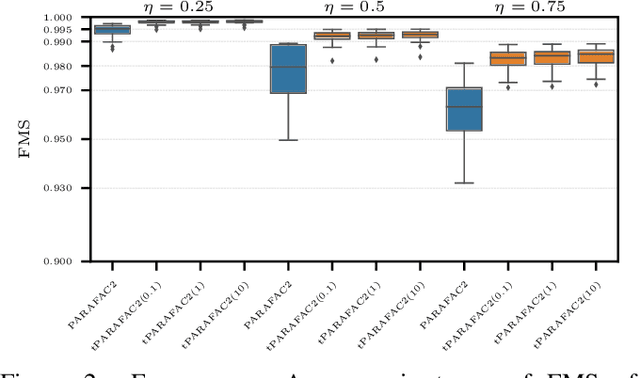
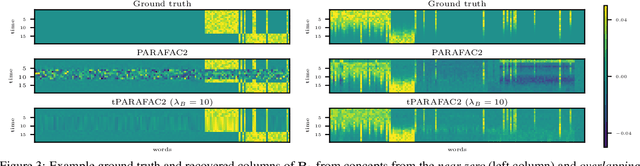
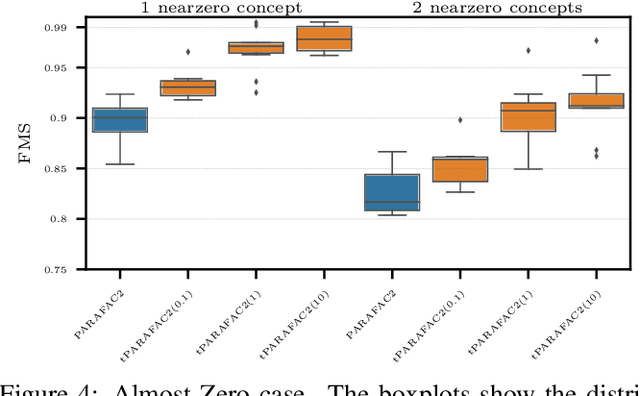
Time-evolving data sets can often be arranged as a higher-order tensor with one of the modes being the time mode. While tensor factorizations have been successfully used to capture the underlying patterns in such higher-order data sets, the temporal aspect is often ignored, allowing for the reordering of time points. In recent studies, temporal regularizers are incorporated in the time mode to tackle this issue. Nevertheless, existing approaches still do not allow underlying patterns to change in time (e.g., spatial changes in the brain, contextual changes in topics). In this paper, we propose temporal PARAFAC2 (tPARAFAC2): a PARAFAC2-based tensor factorization method with temporal regularization to extract gradually evolving patterns from temporal data. Through extensive experiments on synthetic data, we demonstrate that tPARAFAC2 can capture the underlying evolving patterns accurately performing better than PARAFAC2 and coupled matrix factorization with temporal smoothness regularization.

A weighted subspace exponential kernel for support tensor machines

High-dimensional data in the form of tensors are challenging for kernel classification methods. To both reduce the computational complexity and extract informative features, kernels based on low-rank tensor decompositions have been proposed. However, what decisive features of the tensors are exploited by these kernels is often unclear. In this paper we propose a novel kernel that is based on the Tucker decomposition. For this kernel the Tucker factors are computed based on re-weighting of the Tucker matrices with tuneable powers of singular values from the HOSVD decomposition. This provides a mechanism to balance the contribution of the Tucker core and factors of the data. We benchmark support tensor machines with this new kernel on several datasets. First we generate synthetic data where two classes differ in either Tucker factors or core, and compare our novel and previously existing kernels. We show robustness of the new kernel with respect to both classification scenarios. We further test the new method on real-world datasets. The proposed kernel has demonstrated a higher test accuracy than the state-of-the-art tensor train multi-way multi-level kernel, and a significantly lower computational time.

Learning Paths from Signature Tensors

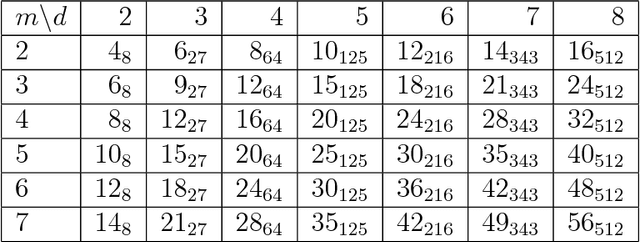
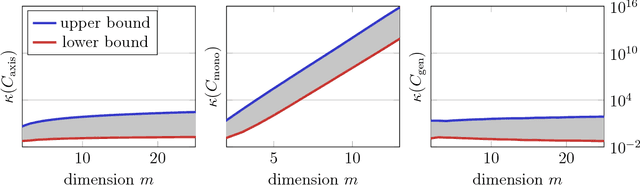
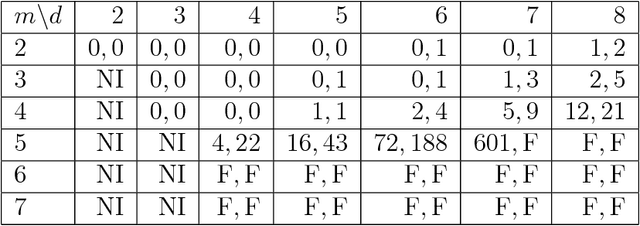
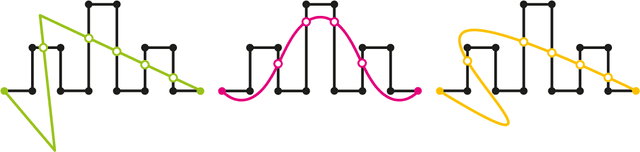
Matrix congruence extends naturally to the setting of tensors. We apply methods from tensor decomposition, algebraic geometry and numerical optimization to this group action. Given a tensor in the orbit of another tensor, we compute a matrix which transforms one to the other. Our primary application is an inverse problem from stochastic analysis: the recovery of paths from their signature tensors of order three. We establish identifiability results and recovery algorithms for piecewise linear paths, polynomial paths, and generic dictionaries. A detailed analysis of the relevant condition numbers is presented. We also compute the shortest path with a given signature tensor.