tPARAFAC2: Tracking evolving patterns in (incomplete) temporal data

Tensor factorizations have been widely used for the task of uncovering patterns in various domains. Often, the input is time-evolving, shifting the goal to tracking the evolution of underlying patterns instead. To adapt to this more complex setting, existing methods incorporate temporal regularization but they either have overly constrained structural requirements or lack uniqueness which is crucial for interpretation. In this paper, in order to capture the underlying evolving patterns, we introduce t(emporal)PARAFAC2 which utilizes temporal smoothness regularization on the evolving factors. We propose an algorithmic framework that employs Alternating Optimization (AO) and the Alternating Direction Method of Multipliers (ADMM) to fit the model. Furthermore, we extend the algorithmic framework to the case of partially observed data. Our numerical experiments on both simulated and real datasets demonstrate the effectiveness of the temporal smoothness regularization, in particular, in the case of data with missing entries. We also provide an extensive comparison of different approaches for handling missing data within the proposed framework.

PARAFAC2-based Coupled Matrix and Tensor Factorizations

Coupled matrix and tensor factorizations (CMTF) have emerged as an effective data fusion tool to jointly analyze data sets in the form of matrices and higher-order tensors. The PARAFAC2 model has shown to be a promising alternative to the CANDECOMP/PARAFAC (CP) tensor model due to its flexibility and capability to handle irregular/ragged tensors. While fusion models based on a PARAFAC2 model coupled with matrix/tensor decompositions have been recently studied, they are limited in terms of possible regularizations and/or types of coupling between data sets. In this paper, we propose an algorithmic framework for fitting PARAFAC2-based CMTF models with the possibility of imposing various constraints on all modes and linear couplings, using Alternating Optimization (AO) and the Alternating Direction Method of Multipliers (ADMM). Through numerical experiments, we demonstrate that the proposed algorithmic approach accurately recovers the underlying patterns using various constraints and linear couplings.

An AO-ADMM approach to constraining PARAFAC2 on all modes

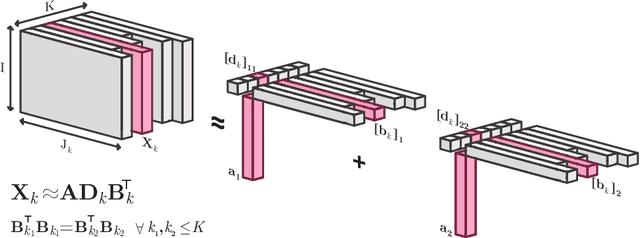
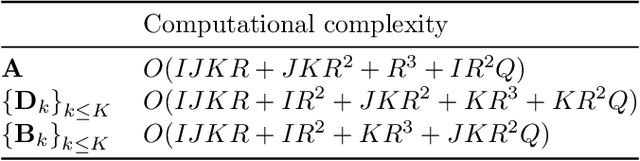
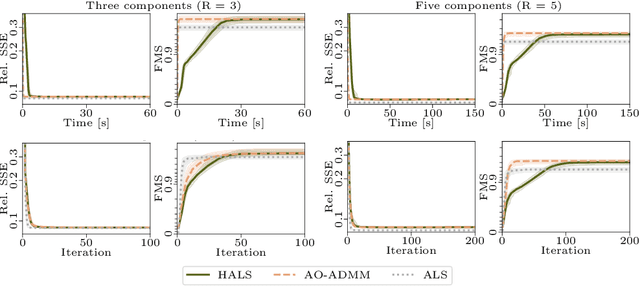
Analyzing multi-way measurements with variations across one mode of the dataset is a challenge in various fields including data mining, neuroscience and chemometrics. For example, measurements may evolve over time or have unaligned time profiles. The PARAFAC2 model has been successfully used to analyze such data by allowing the underlying factor matrices in one mode (i.e., the evolving mode) to change across slices. The traditional approach to fit a PARAFAC2 model is to use an alternating least squares-based algorithm, which handles the constant cross-product constraint of the PARAFAC2 model by implicitly estimating the evolving factor matrices. This approach makes imposing regularization on these factor matrices challenging. There is currently no algorithm to flexibly impose such regularization with general penalty functions and hard constraints. In order to address this challenge and to avoid the implicit estimation, in this paper, we propose an algorithm for fitting PARAFAC2 based on alternating optimization with the alternating direction method of multipliers (AO-ADMM). With numerical experiments on simulated data, we show that the proposed PARAFAC2 AO-ADMM approach allows for flexible constraints, recovers the underlying patterns accurately, and is computationally efficient compared to the state-of-the-art. We also apply our model to a real-world chromatography dataset, and show that constraining the evolving mode improves the interpretability of the extracted patterns.

PARAFAC2 AO-ADMM: Constraints in all modes

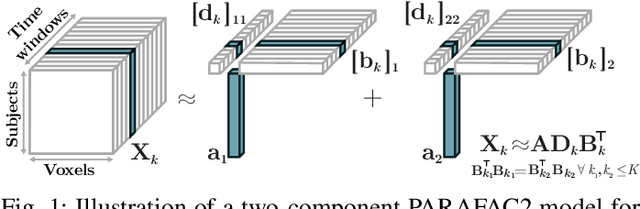
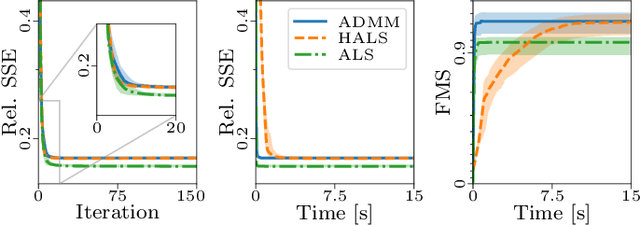
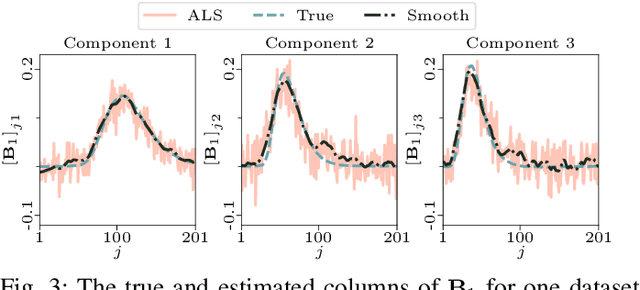
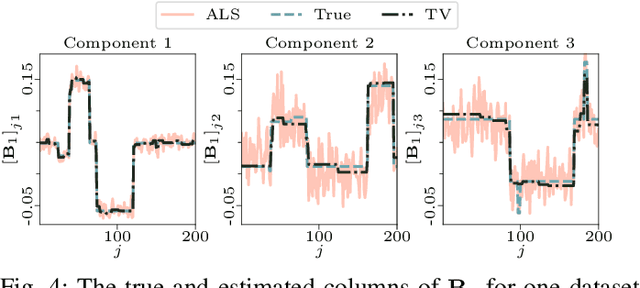
The PARAFAC2 model provides a flexible alternative to the popular CANDECOMP/PARAFAC (CP) model for tensor decompositions. Unlike CP, PARAFAC2 allows factor matrices in one mode (i.e., evolving mode) to change across tensor slices, which has proven useful for applications in different domains such as chemometrics, and neuroscience. However, the evolving mode of the PARAFAC2 model is traditionally modelled implicitly, which makes it challenging to regularise it. Currently, the only way to apply regularisation on that mode is with a flexible coupling approach, which finds the solution through regularised least-squares subproblems. In this work, we instead propose an alternating direction method of multipliers (ADMM)-based algorithm for fitting PARAFAC2 and widen the possible regularisation penalties to any proximable function. Our numerical experiments demonstrate that the proposed ADMM-based approach for PARAFAC2 can accurately recover the underlying components from simulated data while being both computationally efficient and flexible in terms of imposing constraints.

A Flexible Optimization Framework for Regularized Matrix-Tensor Factorizations with Linear Couplings

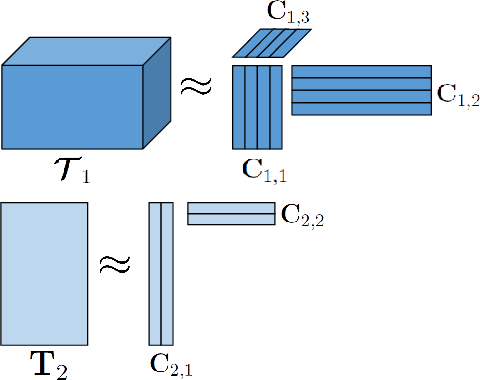
Coupled matrix and tensor factorizations (CMTF) are frequently used to jointly analyze data from multiple sources, also called data fusion. However, different characteristics of datasets stemming from multiple sources pose many challenges in data fusion and require to employ various regularizations, constraints, loss functions and different types of coupling structures between datasets. In this paper, we propose a flexible algorithmic framework for coupled matrix and tensor factorizations which utilizes Alternating Optimization (AO) and the Alternating Direction Method of Multipliers (ADMM). The framework facilitates the use of a variety of constraints, loss functions and couplings with linear transformations in a seamless way. Numerical experiments on simulated and real datasets demonstrate that the proposed approach is accurate, and computationally efficient with comparable or better performance than available CMTF methods for Frobenius norm loss, while being more flexible. Using Kullback-Leibler divergence on count data, we demonstrate that the algorithm yields accurate results also for other loss functions.