Barwise Music Structure Analysis with the Correlation Block-Matching Segmentation Algorithm

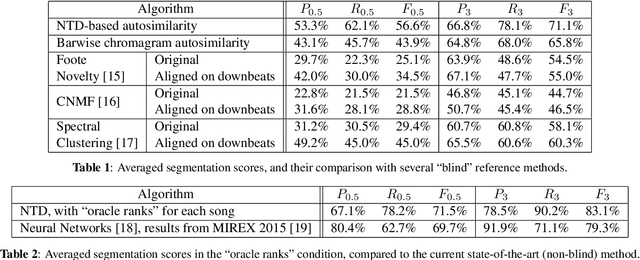
Music Structure Analysis (MSA) is a Music Information Retrieval task consisting of representing a song in a simplified, organized manner by breaking it down into sections typically corresponding to ``chorus'', ``verse'', ``solo'', etc. In this work, we extend an MSA algorithm called the Correlation Block-Matching (CBM) algorithm introduced by (Marmoret et al., 2020, 2022b). The CBM algorithm is a dynamic programming algorithm that segments self-similarity matrices, which are a standard description used in MSA and in numerous other applications. In this work, self-similarity matrices are computed from the feature representation of an audio signal and time is sampled at the bar-scale. This study examines three different standard similarity functions for the computation of self-similarity matrices. Results show that, in optimal conditions, the proposed algorithm achieves a level of performance which is competitive with supervised state-of-the-art methods while only requiring knowledge of bar positions. In addition, the algorithm is made open-source and is highly customizable.

Polytopic Analysis of Music

Structural segmentation of music refers to the task of finding a symbolic representation of the organisation of a song, reducing the musical flow to a partition of non-overlapping segments. Under this definition, the musical structure may not be unique, and may even be ambiguous. One way to resolve that ambiguity is to see this task as a compression process, and to consider the musical structure as the optimization of a given compression criteria. In that viewpoint, C. Guichaoua developed a compression-driven model for retrieving the musical structure, based on the "System and Contrast" model, and on polytopes, which are extension of nhypercubes. We present this model, which we call "polytopic analysis of music", along with a new opensource dedicated toolbox called MusicOnPolytopes (in Python). This model is also extended to the use of the Tonnetz as a relation system. Structural segmentation experiments are conducted on the RWC Pop dataset. Results show improvements compared to the previous ones, presented by C. Guichaoua.

Convolutive Block-Matching Segmentation Algorithm with Application to Music Structure Analysis

Music Structure Analysis (MSA) consists of representing a song in sections (such as ``chorus'', ``verse'', ``solo'' etc), and can be seen as the retrieval of a simplified organization of the song. This work presents a new algorithm, called Convolutive Block-Matching (CBM) algorithm, devoted to MSA. In particular, the CBM algorithm is a dynamic programming algorithm, applying on autosimilarity matrices, a standard tool in MSA. In this work, autosimilarity matrices are computed from the feature representation of an audio signal, and time is sampled on the barscale. We study three different similarity functions for the computation of autosimilarity matrices. We report that the proposed algorithm achieves a level of performance competitive to that of supervised state-of-the-art methods on 3 among 4 metrics, while being fully unsupervised.

Semi-Supervised Convolutive NMF for Automatic Music Transcription

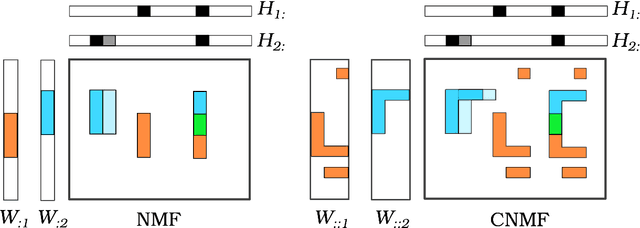
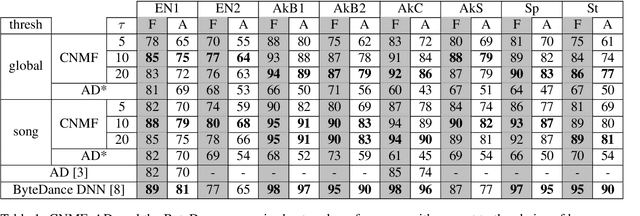
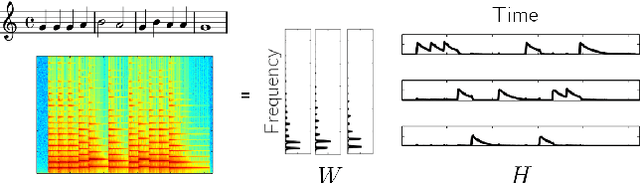
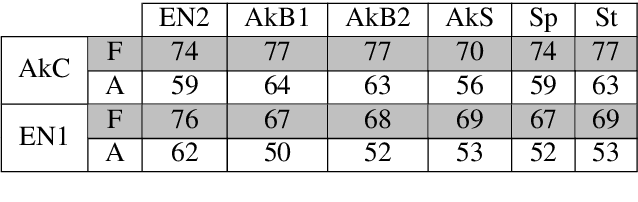
Automatic Music Transcription, which consists in transforming an audio recording of a musical performance into symbolic format, remains a difficult Music Information Retrieval task. In this work, we propose a semi-supervised approach using low-rank matrix factorization techniques, in particular Convolutive Nonnegative Matrix Factorization. In the semi-supervised setting, only a single recording of each individual notes is required. We show on the MAPS dataset that the proposed semi-supervised CNMF method performs better than state-of-the-art low-rank factorization techniques and a little worse than supervised deep learning state-of-the-art methods, while however suffering from generalization issues.

Barwise Compression Schemes for Audio-Based Music Structure Analysis

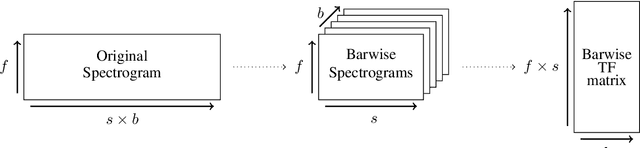
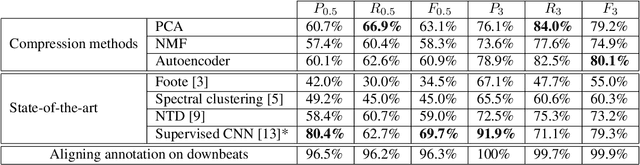
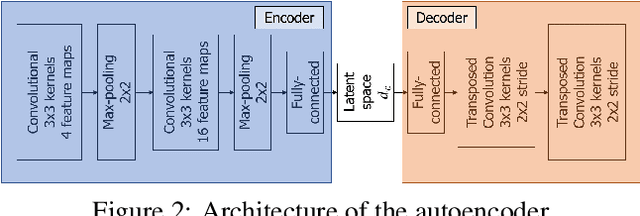
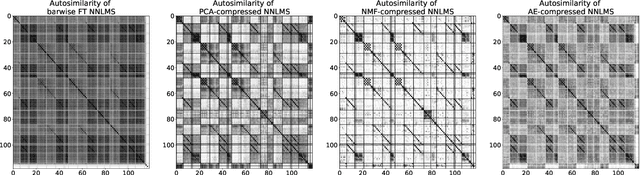
Music Structure Analysis (MSA) consists in segmenting a music piece in several distinct sections. We approach MSA within a compression framework, under the hypothesis that the structure is more easily revealed by a simplified representation of the original content of the song. More specifically, under the hypothesis that MSA is correlated with similarities occurring at the bar scale, linear and non-linear compression schemes can be applied to barwise audio signals. Compressed representations capture the most salient components of the different bars in the song and are then used to infer the song structure using a dynamic programming algorithm. This work explores both low-rank approximation models such as Principal Component Analysis or Nonnegative Matrix Factorization and "piece-specific" Auto-Encoding Neural Networks, with the objective to learn latent representations specific to a given song. Such approaches do not rely on supervision nor annotations, which are well-known to be tedious to collect and possibly ambiguous in MSA description. In our experiments, several unsupervised compression schemes achieve a level of performance comparable to that of state-of-the-art supervised methods (for 3s tolerance) on the RWC-Pop dataset, showcasing the importance of the barwise compression processing for MSA.

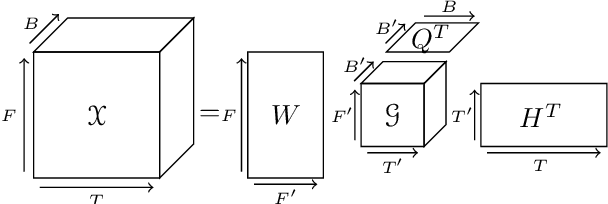
Nonnegative Tucker Decomposition with Beta-divergence for Music Structure Analysis of audio signals

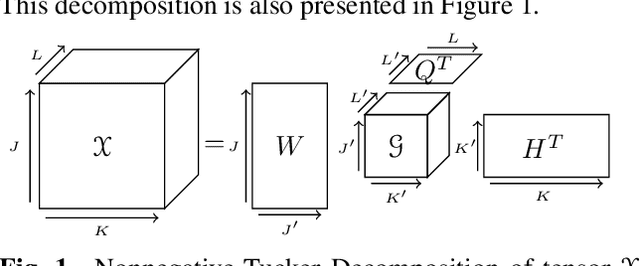
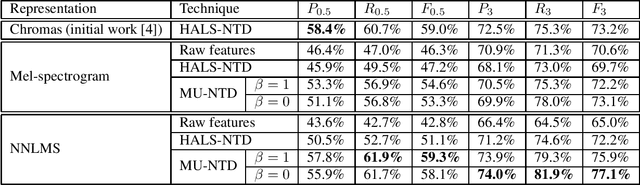
Nonnegative Tucker Decomposition (NTD), a tensor decomposition model, has received increased interest in the recent years because of its ability to blindly extract meaningful patterns in tensor data. Nevertheless, existing algorithms to compute NTD are mostly designed for the Euclidean loss. On the other hand, NTD has recently proven to be a powerful tool in Music Information Retrieval. This work proposes a Multiplicative Updates algorithm to compute NTD with the beta-divergence loss, often considered a better loss for audio processing. We notably show how to implement efficiently the multiplicative rules using tensor algebra, a naive approach being intractable. Finally, we show on a Music Structure Analysis task that unsupervised NTD fitted with beta-divergence loss outperforms earlier results obtained with the Euclidean loss.

Exploring single-song autoencoding schemes for audio-based music structure analysis

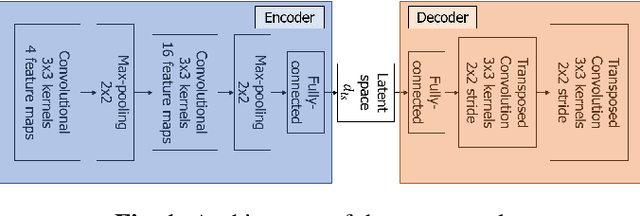
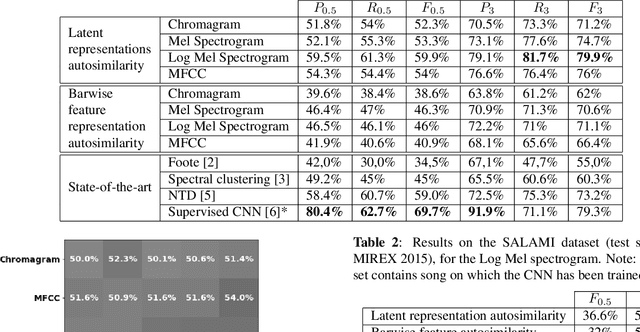
The ability of deep neural networks to learn complex data relations and representations is established nowadays, but it generally relies on large sets of training data. This work explores a "piece-specific" autoencoding scheme, in which a low-dimensional autoencoder is trained to learn a latent/compressed representation specific to a given song, which can then be used to infer the song structure. Such a model does not rely on supervision nor annotations, which are well-known to be tedious to collect and often ambiguous in Music Structure Analysis. We report that the proposed unsupervised auto-encoding scheme achieves the level of performance of supervised state-of-the-art methods with 3 seconds tolerance when using a Log Mel spectrogram representation on the RWC-Pop dataset.

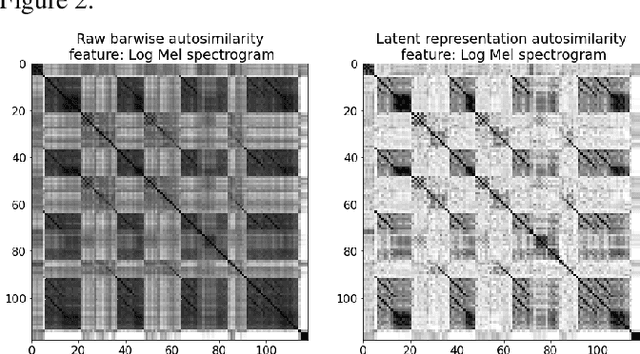
Uncovering audio patterns in music with Nonnegative Tucker Decomposition for structural segmentation

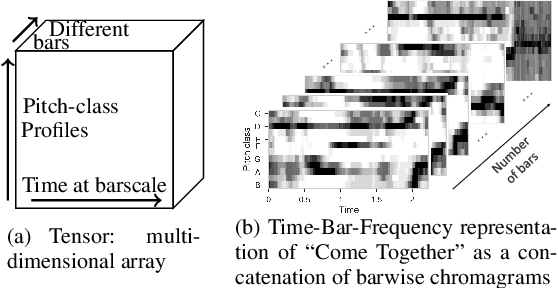
Recent work has proposed the use of tensor decomposition to model repetitions and to separate tracks in loop-based electronic music. The present work investigates further on the ability of Nonnegative Tucker Decompositon (NTD) to uncover musical patterns and structure in pop songs in their audio form. Exploiting the fact that NTD tends to express the content of bars as linear combinations of a few patterns, we illustrate the ability of the decomposition to capture and single out repeated motifs in the corresponding compressed space, which can be interpreted from a musical viewpoint. The resulting features also turn out to be efficient for structural segmentation, leading to experimental results on the RWC Pop data set which are potentially challenging state-of-the-art approaches that rely on extensive example-based learning schemes.

Identifiability of Low-Rank Sparse Component Analysis

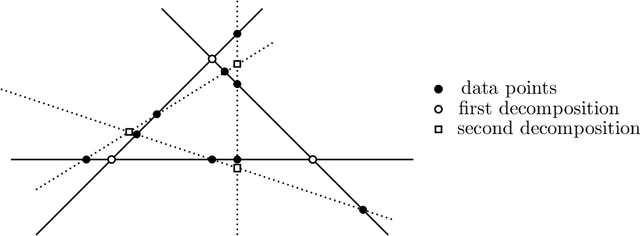
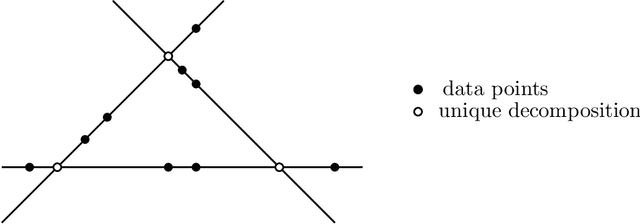
Sparse component analysis (SCA) is the following problem: Given an input matrix $M$ and an integer $r$, find a dictionary $D$ with $r$ columns and a sparse matrix $B$ with $r$ rows such that $M \approx DB$. A key issue in SCA is identifiability, that is, characterizing the conditions under which $D$ and $B$ are essentially unique (that is, they are unique up to permutation and scaling of the columns of $D$ and rows of $B$). Although SCA has been vastly investigated in the last two decades, only a few works have tackled this issue in the deterministic scenario, and no work provides reasonable bounds in the minimum number of data points (that is, columns of $M$) that leads to identifiability. In this work, we provide new results in the deterministic scenario when the data has a low-rank structure, that is, when $D$ has rank $r$, drastically improving with respect to previous results. In particular, we show that if each column of $B$ contains at least $s$ zeros then $\mathcal{O}(r^3/s^2)$ data points are sufficient to obtain an essentially unique decomposition, as long as these data points are well spread among the subspaces spanned by $r-1$ columns of $D$. This implies for example that for a fixed proportion of zeros (constant and independent of $r$, e.g., 10\% of zero entries in $B$), one only requires $O(r)$ data points to guarantee identifiability.

Dictionary-based Tensor Canonical Polyadic Decomposition

To ensure interpretability of extracted sources in tensor decomposition, we introduce in this paper a dictionary-based tensor canonical polyadic decomposition which enforces one factor to belong exactly to a known dictionary. A new formulation of sparse coding is proposed which enables high dimensional tensors dictionary-based canonical polyadic decomposition. The benefits of using a dictionary in tensor decomposition models are explored both in terms of parameter identifiability and estimation accuracy. Performances of the proposed algorithms are evaluated on the decomposition of simulated data and the unmixing of hyperspectral images.