tPARAFAC2: Tracking evolving patterns in (incomplete) temporal data

Tensor factorizations have been widely used for the task of uncovering patterns in various domains. Often, the input is time-evolving, shifting the goal to tracking the evolution of underlying patterns instead. To adapt to this more complex setting, existing methods incorporate temporal regularization but they either have overly constrained structural requirements or lack uniqueness which is crucial for interpretation. In this paper, in order to capture the underlying evolving patterns, we introduce t(emporal)PARAFAC2 which utilizes temporal smoothness regularization on the evolving factors. We propose an algorithmic framework that employs Alternating Optimization (AO) and the Alternating Direction Method of Multipliers (ADMM) to fit the model. Furthermore, we extend the algorithmic framework to the case of partially observed data. Our numerical experiments on both simulated and real datasets demonstrate the effectiveness of the temporal smoothness regularization, in particular, in the case of data with missing entries. We also provide an extensive comparison of different approaches for handling missing data within the proposed framework.

A Time-aware tensor decomposition for tracking evolving patterns

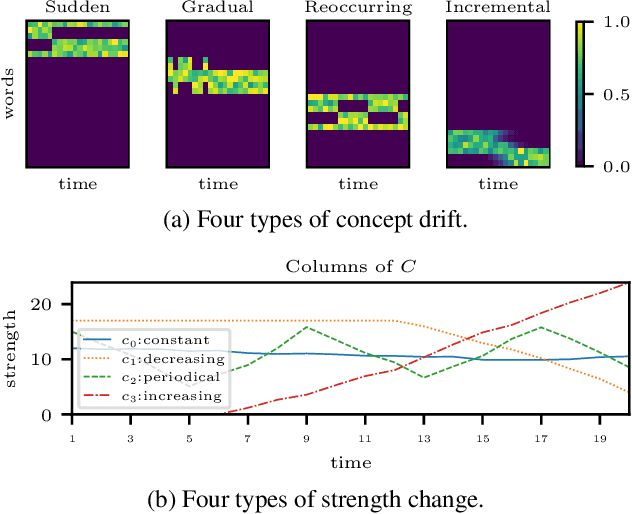
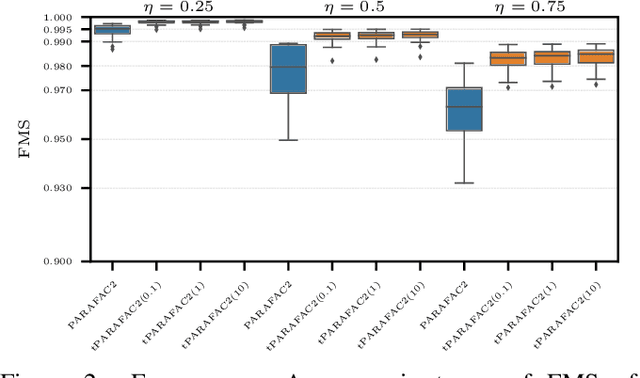
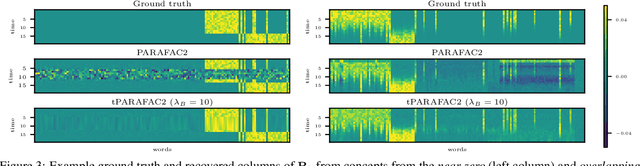
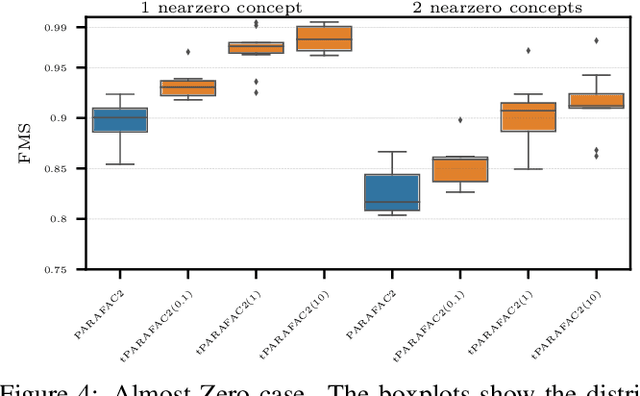
Time-evolving data sets can often be arranged as a higher-order tensor with one of the modes being the time mode. While tensor factorizations have been successfully used to capture the underlying patterns in such higher-order data sets, the temporal aspect is often ignored, allowing for the reordering of time points. In recent studies, temporal regularizers are incorporated in the time mode to tackle this issue. Nevertheless, existing approaches still do not allow underlying patterns to change in time (e.g., spatial changes in the brain, contextual changes in topics). In this paper, we propose temporal PARAFAC2 (tPARAFAC2): a PARAFAC2-based tensor factorization method with temporal regularization to extract gradually evolving patterns from temporal data. Through extensive experiments on synthetic data, we demonstrate that tPARAFAC2 can capture the underlying evolving patterns accurately performing better than PARAFAC2 and coupled matrix factorization with temporal smoothness regularization.