Modeling Eye Gaze Velocity Trajectories using GANs with Spectral Loss for Enhanced Fidelity

Accurate modeling of eye gaze dynamics is essential for advancement in human-computer interaction, neurological diagnostics, and cognitive research. Traditional generative models like Markov models often fail to capture the complex temporal dependencies and distributional nuance inherent in eye gaze trajectories data. This study introduces a GAN framework employing LSTM and CNN generators and discriminators to generate high-fidelity synthetic eye gaze velocity trajectories. We conducted a comprehensive evaluation of four GAN architectures: CNN-CNN, LSTM-CNN, CNN-LSTM, and LSTM-LSTM trained under two conditions: using only adversarial loss and using a weighted combination of adversarial and spectral losses. Our findings reveal that the LSTM-CNN architecture trained with this new loss function exhibits the closest alignment to the real data distribution, effectively capturing both the distribution tails and the intricate temporal dependencies. The inclusion of spectral regularization significantly enhances the GANs ability to replicate the spectral characteristics of eye gaze movements, leading to a more stable learning process and improved data fidelity. Comparative analysis with an HMM optimized to four hidden states further highlights the advantages of the LSTM-CNN GAN. Statistical metrics show that the HMM-generated data significantly diverges from the real data in terms of mean, standard deviation, skewness, and kurtosis. In contrast, the LSTM-CNN model closely matches the real data across these statistics, affirming its capacity to model the complexity of eye gaze dynamics effectively. These results position the spectrally regularized LSTM-CNN GAN as a robust tool for generating synthetic eye gaze velocity data with high fidelity.

Modeling stochastic eye tracking data: A comparison of quantum generative adversarial networks and Markov models

We explore the use of quantum generative adversarial networks QGANs for modeling eye movement velocity data. We assess whether the advanced computational capabilities of QGANs can enhance the modeling of complex stochastic distribution beyond the traditional mathematical models, particularly the Markov model. The findings indicate that while QGANs demonstrate potential in approximating complex distributions, the Markov model consistently outperforms in accurately replicating the real data distribution. This comparison underlines the challenges and avenues for refinement in time series data generation using quantum computing techniques. It emphasizes the need for further optimization of quantum models to better align with real-world data characteristics.

A Time-aware tensor decomposition for tracking evolving patterns

Time-evolving data sets can often be arranged as a higher-order tensor with one of the modes being the time mode. While tensor factorizations have been successfully used to capture the underlying patterns in such higher-order data sets, the temporal aspect is often ignored, allowing for the reordering of time points. In recent studies, temporal regularizers are incorporated in the time mode to tackle this issue. Nevertheless, existing approaches still do not allow underlying patterns to change in time (e.g., spatial changes in the brain, contextual changes in topics). In this paper, we propose temporal PARAFAC2 (tPARAFAC2): a PARAFAC2-based tensor factorization method with temporal regularization to extract gradually evolving patterns from temporal data. Through extensive experiments on synthetic data, we demonstrate that tPARAFAC2 can capture the underlying evolving patterns accurately performing better than PARAFAC2 and coupled matrix factorization with temporal smoothness regularization.

Assessing the robustness of critical behavior in stochastic cellular automata

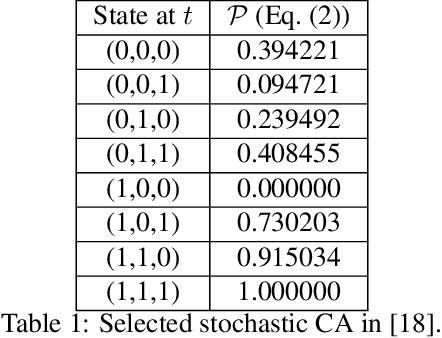
There is evidence that biological systems, such as the brain, work at a critical regime robust to noise, and are therefore able to remain in it under perturbations. In this work, we address the question of robustness of critical systems to noise. In particular, we investigate the robustness of stochastic cellular automata (CAs) at criticality. A stochastic CA is one of the simplest stochastic models showing criticality. The transition state of stochastic CA is defined through a set of probabilities. We systematically perturb the probabilities of an optimal stochastic CA known to produce critical behavior, and we report that such a CA is able to remain in a critical regime up to a certain degree of noise. We present the results using error metrics of the resulting power-law fitting, such as Kolmogorov-Smirnov statistic and Kullback-Leibler divergence. We discuss the implication of our results in regards to future realization of brain-inspired artificial intelligence systems.