Efficient Algorithms for Regularized Nonnegative Scale-invariant Low-rank Approximation Models

Regularized nonnegative low-rank approximations such as sparse Nonnegative Matrix Factorization or sparse Nonnegative Tucker Decomposition are an important branch of dimensionality reduction models with enhanced interpretability. However, from a practical perspective, the choice of regularizers and regularization coefficients, as well as the design of efficient algorithms, is challenging because of the multifactor nature of these models and the lack of theory to back these choices. This paper aims at improving upon these issues. By studying a more general model called the Homogeneous Regularized Scale-Invariant, we prove that the scale-invariance inherent to low-rank approximation models causes an implicit regularization with both unexpected beneficial and detrimental effects. This observation allows to better understand the effect of regularization functions in low-rank approximation models, to guide the choice of the regularization hyperparameters, and to design balancing strategies to enhance the convergence speed of dedicated optimization algorithms. Some of these results were already known but restricted to specific instances of regularized low-rank approximations. We also derive a generic Majorization Minimization algorithm that handles many regularized nonnegative low-rank approximations, with convergence guarantees. We showcase our contributions on sparse Nonnegative Matrix Factorization, ridge-regularized Canonical Polyadic decomposition and sparse Nonnegative Tucker Decomposition.

Block Majorization Minimization with Extrapolation and Application to $β$-NMF

We propose a Block Majorization Minimization method with Extrapolation (BMMe) for solving a class of multi-convex optimization problems. The extrapolation parameters of BMMe are updated using a novel adaptive update rule. By showing that block majorization minimization can be reformulated as a block mirror descent method, with the Bregman divergence adaptively updated at each iteration, we establish subsequential convergence for BMMe. We use this method to design efficient algorithms to tackle nonnegative matrix factorization problems with the $\beta$-divergences ($\beta$-NMF) for $\beta\in [1,2]$. These algorithms, which are multiplicative updates with extrapolation, benefit from our novel results that offer convergence guarantees. We also empirically illustrate the significant acceleration of BMMe for $\beta$-NMF through extensive experiments.

Deep Nonnegative Matrix Factorization with Beta Divergences

Deep Nonnegative Matrix Factorization (deep NMF) has recently emerged as a valuable technique for extracting multiple layers of features across different scales. However, all existing deep NMF models and algorithms have primarily centered their evaluation on the least squares error, which may not be the most appropriate metric for assessing the quality of approximations on diverse datasets. For instance, when dealing with data types such as audio signals and documents, it is widely acknowledged that $\beta$-divergences offer a more suitable alternative. In this paper, we develop new models and algorithms for deep NMF using $\beta$-divergences. Subsequently, we apply these techniques to the extraction of facial features, the identification of topics within document collections, and the identification of materials within hyperspectral images.

NAG-GS: Semi-Implicit, Accelerated and Robust Stochastic Optimizers

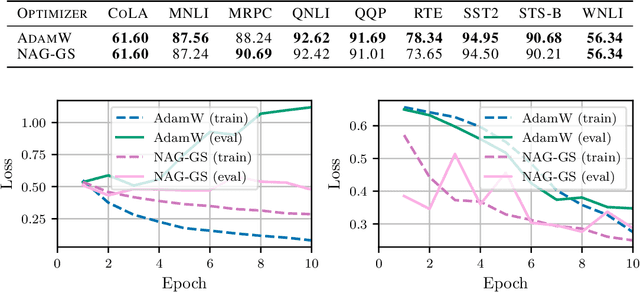
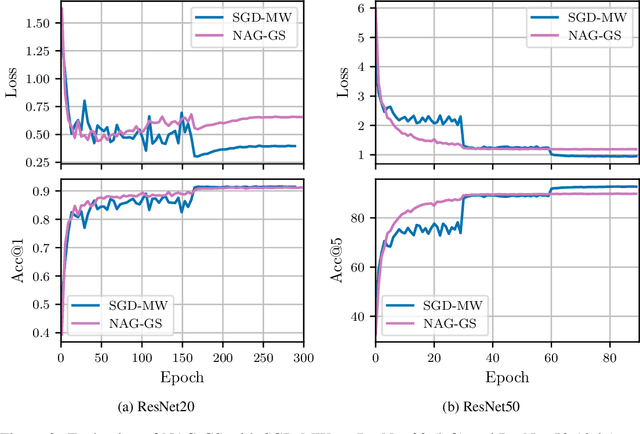
Classical machine learning models such as deep neural networks are usually trained by using Stochastic Gradient Descent-based (SGD) algorithms. The classical SGD can be interpreted as a discretization of the stochastic gradient flow. In this paper we propose a novel, robust and accelerated stochastic optimizer that relies on two key elements: (1) an accelerated Nesterov-like Stochastic Differential Equation (SDE) and (2) its semi-implicit Gauss-Seidel type discretization. The convergence and stability of the obtained method, referred to as NAG-GS, are first studied extensively in the case of the minimization of a quadratic function. This analysis allows us to come up with an optimal step size (or learning rate) in terms of rate of convergence while ensuring the stability of NAG-GS. This is achieved by the careful analysis of the spectral radius of the iteration matrix and the covariance matrix at stationarity with respect to all hyperparameters of our method. We show that NAG-GS is competitive with state-of-the-art methods such as momentum SGD with weight decay and AdamW for the training of machine learning models such as the logistic regression model, the residual networks models on standard computer vision datasets, and Transformers in the frame of the GLUE benchmark.

Nonnegative Tucker Decomposition with Beta-divergence for Music Structure Analysis of audio signals

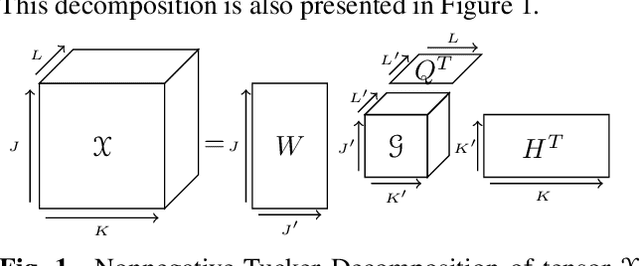
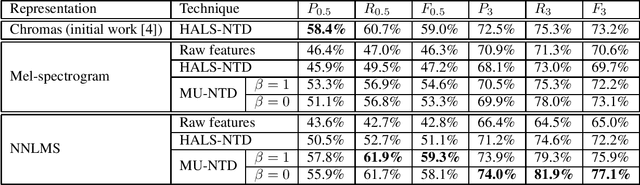
Nonnegative Tucker Decomposition (NTD), a tensor decomposition model, has received increased interest in the recent years because of its ability to blindly extract meaningful patterns in tensor data. Nevertheless, existing algorithms to compute NTD are mostly designed for the Euclidean loss. On the other hand, NTD has recently proven to be a powerful tool in Music Information Retrieval. This work proposes a Multiplicative Updates algorithm to compute NTD with the beta-divergence loss, often considered a better loss for audio processing. We notably show how to implement efficiently the multiplicative rules using tensor algebra, a naive approach being intractable. Finally, we show on a Music Structure Analysis task that unsupervised NTD fitted with beta-divergence loss outperforms earlier results obtained with the Euclidean loss.

Multiplicative Updates for NMF with $β$-Divergences under Disjoint Equality Constraints

Nonnegative matrix factorization (NMF) is the problem of approximating an input nonnegative matrix, $V$, as the product of two smaller nonnegative matrices, $W$ and $H$. In this paper, we introduce a general framework to design multiplicative updates (MU) for NMF based on $\beta$-divergences ($\beta$-NMF) with disjoint equality constraints, and with penalty terms in the objective function. By disjoint, we mean that each variable appears in at most one equality constraint. Our MU satisfy the set of constraints after each update of the variables during the optimization process, while guaranteeing that the objective function decreases monotonically. We showcase this framework on three NMF models, and show that it competes favorably the state of the art: (1)~$\beta$-NMF with sum-to-one constraints on the columns of $H$, (2) minimum-volume $\beta$-NMF with sum-to-one constraints on the columns of $W$, and (3) sparse $\beta$-NMF with $\ell_2$-norm constraints on the columns of $W$.

Blind Audio Source Separation with Minimum-Volume Beta-Divergence NMF

Considering a mixed signal composed of various audio sources and recorded with a single microphone, we consider on this paper the blind audio source separation problem which consists in isolating and extracting each of the sources. To perform this task, nonnegative matrix factorization (NMF) based on the Kullback-Leibler and Itakura-Saito $\beta$-divergences is a standard and state-of-the-art technique that uses the time-frequency representation of the signal. We present a new NMF model better suited for this task. It is based on the minimization of $\beta$-divergences along with a penalty term that promotes the columns of the dictionary matrix to have a small volume. Under some mild assumptions and in noiseless conditions, we prove that this model is provably able to identify the sources. In order to solve this problem, we propose multiplicative updates whose derivations are based on the standard majorization-minimization framework. We show on several numerical experiments that our new model is able to obtain more interpretable results than standard NMF models. Moreover, we show that it is able to recover the sources even when the number of sources present into the mixed signal is overestimated. In fact, our model automatically sets sources to zero in this situation, hence performs model order selection automatically.

Distributionally Robust and Multi-Objective Nonnegative Matrix Factorization

Nonnegative matrix factorization (NMF) is a linear dimensionality reduction technique for analyzing nonnegative data. A key aspect of NMF is the choice of the objective function that depends on the noise model (or statistics of the noise) assumed on the data. In many applications, the noise model is unknown and difficult to estimate. In this paper, we define a multi-objective NMF (MO-NMF) problem, where several objectives are combined within the same NMF model. We propose to use Lagrange duality to judiciously optimize for a set of weights to be used within the framework of the weighted-sum approach, that is, we minimize a single objective function which is a weighted sum of the all objective functions. We design a simple algorithm using multiplicative updates to minimize this weighted sum. We show how this can be used to find distributionally robust NMF (DR-NMF) solutions, that is, solutions that minimize the largest error among all objectives. We illustrate the effectiveness of this approach on synthetic, document and audio datasets. The results show that DR-NMF is robust to our incognizance of the noise model of the NMF problem.