Ultrasound Image Enhancement with the Variance of Diffusion Models

Ultrasound imaging, despite its widespread use in medicine, often suffers from various sources of noise and artifacts that impact the signal-to-noise ratio and overall image quality. Enhancing ultrasound images requires a delicate balance between contrast, resolution, and speckle preservation. This paper introduces a novel approach that integrates adaptive beamforming with denoising diffusion-based variance imaging to address this challenge. By applying Eigenspace-Based Minimum Variance (EBMV) beamforming and employing a denoising diffusion model fine-tuned on ultrasound data, our method computes the variance across multiple diffusion-denoised samples to produce high-quality despeckled images. This approach leverages both the inherent multiplicative noise of ultrasound and the stochastic nature of diffusion models. Experimental results on a publicly available dataset demonstrate the effectiveness of our method in achieving superior image reconstructions from single plane-wave acquisitions. The code is available at: https://github.com/Yuxin-Zhang-Jasmine/IUS2024_Diffusion.

Ultrasound Imaging based on the Variance of a Diffusion Restoration Model

Despite today's prevalence of ultrasound imaging in medicine, ultrasound signal-to-noise ratio is still affected by several sources of noise and artefacts. Moreover, enhancing ultrasound image quality involves balancing concurrent factors like contrast, resolution, and speckle preservation. Recently, there has been progress in both model-based and learning-based approaches addressing the problem of ultrasound image reconstruction. Bringing the best from both worlds, we propose a hybrid reconstruction method combining an ultrasound linear direct model with a learning-based prior coming from a generative Denoising Diffusion model. More specifically, we rely on the unsupervised fine-tuning of a pre-trained Denoising Diffusion Restoration Model (DDRM). Given the nature of multiplicative noise inherent to ultrasound, this paper proposes an empirical model to characterize the stochasticity of diffusion reconstruction of ultrasound images, and shows the interest of its variance as an echogenicity map estimator. We conduct experiments on synthetic, in-vitro, and in-vivo data, demonstrating the efficacy of our variance imaging approach in achieving high-quality image reconstructions from single plane-wave acquisitions and in comparison to state-of-the-art methods.

Diffusion Reconstruction of Ultrasound Images with Informative Uncertainty

Despite its wide use in medicine, ultrasound imaging faces several challenges related to its poor signal-to-noise ratio and several sources of noise and artefacts. Enhancing ultrasound image quality involves balancing concurrent factors like contrast, resolution, and speckle preservation. In recent years, there has been progress both in model-based and learning-based approaches to improve ultrasound image reconstruction. Bringing the best from both worlds, we propose a hybrid approach leveraging advances in diffusion models. To this end, we adapt Denoising Diffusion Restoration Models (DDRM) to incorporate ultrasound physics through a linear direct model and an unsupervised fine-tuning of the prior diffusion model. We conduct comprehensive experiments on simulated, in-vitro, and in-vivo data, demonstrating the efficacy of our approach in achieving high-quality image reconstructions from a single plane wave input and in comparison to state-of-the-art methods. Finally, given the stochastic nature of the method, we analyse in depth the statistical properties of single and multiple-sample reconstructions, experimentally show the informativeness of their variance, and provide an empirical model relating this behaviour to speckle noise. The code and data are available at: (upon acceptance).

Ultrasound Image Reconstruction with Denoising Diffusion Restoration Models

Ultrasound image reconstruction can be approximately cast as a linear inverse problem that has traditionally been solved with penalized optimization using the $l_1$ or $l_2$ norm, or wavelet-based terms. However, such regularization functions often struggle to balance the sparsity and the smoothness. A promising alternative is using learned priors to make the prior knowledge closer to reality. In this paper, we rely on learned priors under the framework of Denoising Diffusion Restoration Models (DDRM), initially conceived for restoration tasks with natural images. We propose and test two adaptions of DDRM to ultrasound inverse problem models, DRUS and WDRUS. Our experiments on synthetic and PICMUS data show that from a single plane wave our method can achieve image quality comparable to or better than DAS and state-of-the-art methods. The code is available at: https://github.com/Yuxin-Zhang-Jasmine/DRUS-v1.

A Partially Collapsed Sampler for Unsupervised Nonnegative Spike Train Restoration

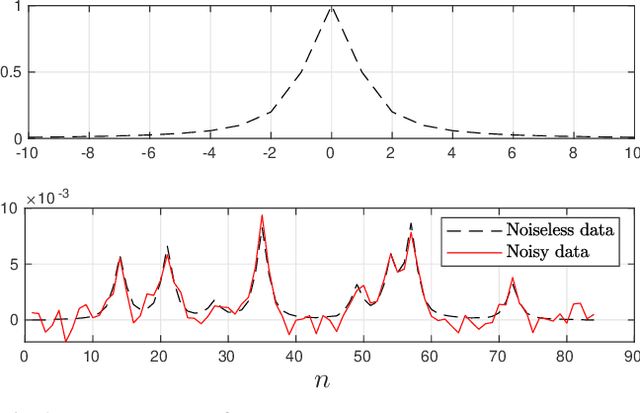
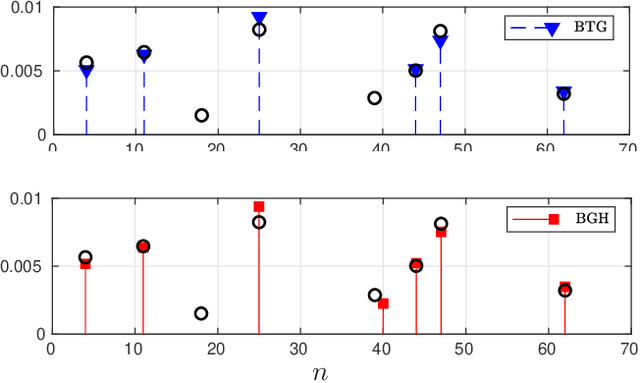
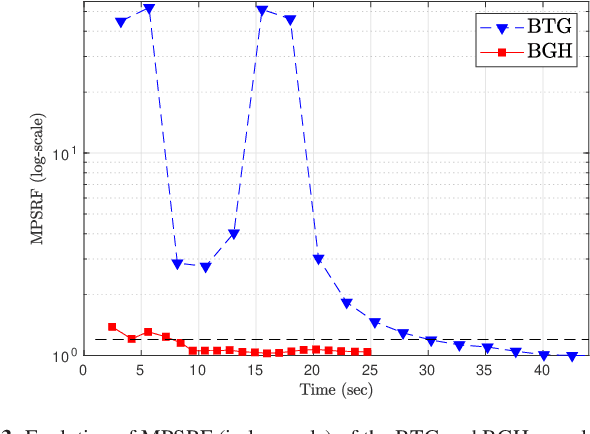
In this paper the problem of restoration of non-negative sparse signals is addressed in the Bayesian framework. We introduce a new probabilistic hierarchical prior, based on the Generalized Hyperbolic (GH) distribution, which explicitly accounts for sparsity. This new prior allows on the one hand, to take into account the non-negativity. And on the other hand, thanks to the decomposition of GH distributions as continuous Gaussian mean-variance mixture, allows us to propose a partially collapsed Gibbs sampler (PCGS), which is shown to be more efficient in terms of convergence time than the classical Gibbs sampler.

SLS : a new greedy algorithm with an $\ell_1$-norm selection rule

In this paper, we propose a new greedy algorithm for sparse approximation, called SLS for Single L_1 Selection. SLS essentially consists of a greedy forward strategy, where the selection rule of a new component at each iteration is based on solving a least-squares optimization problem, penalized by the L_1 norm of the remaining variables. Then, the component with maximum amplitude is selected. Simulation results on difficult sparse deconvolution problems involving a highly correlated dictionary reveal the efficiency of the method, which outperforms popular greedy algorithms and Basis Pursuit Denoising when the solution is sparse.

Multiplicative Updates for NMF with $β$-Divergences under Disjoint Equality Constraints

Nonnegative matrix factorization (NMF) is the problem of approximating an input nonnegative matrix, $V$, as the product of two smaller nonnegative matrices, $W$ and $H$. In this paper, we introduce a general framework to design multiplicative updates (MU) for NMF based on $\beta$-divergences ($\beta$-NMF) with disjoint equality constraints, and with penalty terms in the objective function. By disjoint, we mean that each variable appears in at most one equality constraint. Our MU satisfy the set of constraints after each update of the variables during the optimization process, while guaranteeing that the objective function decreases monotonically. We showcase this framework on three NMF models, and show that it competes favorably the state of the art: (1)~$\beta$-NMF with sum-to-one constraints on the columns of $H$, (2) minimum-volume $\beta$-NMF with sum-to-one constraints on the columns of $W$, and (3) sparse $\beta$-NMF with $\ell_2$-norm constraints on the columns of $W$.

Homotopy based algorithms for $\ell_0$-regularized least-squares

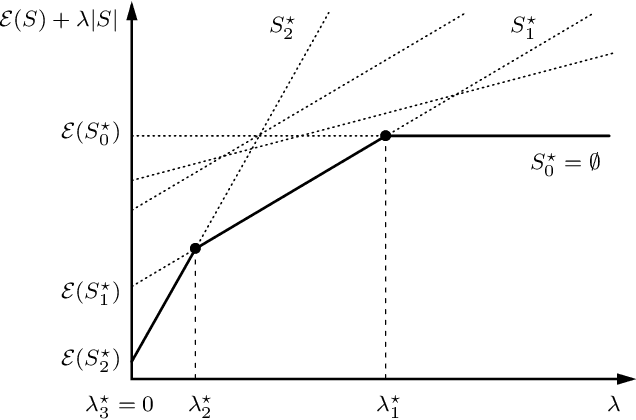
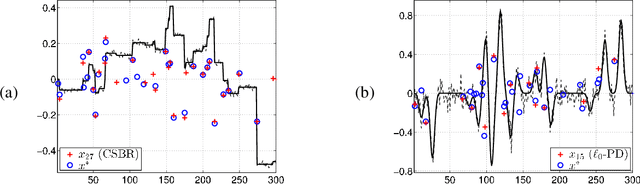
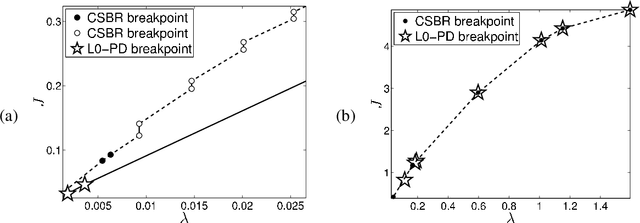
Sparse signal restoration is usually formulated as the minimization of a quadratic cost function $\|y-Ax\|_2^2$, where A is a dictionary and x is an unknown sparse vector. It is well-known that imposing an $\ell_0$ constraint leads to an NP-hard minimization problem. The convex relaxation approach has received considerable attention, where the $\ell_0$-norm is replaced by the $\ell_1$-norm. Among the many efficient $\ell_1$ solvers, the homotopy algorithm minimizes $\|y-Ax\|_2^2+\lambda\|x\|_1$ with respect to x for a continuum of $\lambda$'s. It is inspired by the piecewise regularity of the $\ell_1$-regularization path, also referred to as the homotopy path. In this paper, we address the minimization problem $\|y-Ax\|_2^2+\lambda\|x\|_0$ for a continuum of $\lambda$'s and propose two heuristic search algorithms for $\ell_0$-homotopy. Continuation Single Best Replacement is a forward-backward greedy strategy extending the Single Best Replacement algorithm, previously proposed for $\ell_0$-minimization at a given $\lambda$. The adaptive search of the $\lambda$-values is inspired by $\ell_1$-homotopy. $\ell_0$ Regularization Path Descent is a more complex algorithm exploiting the structural properties of the $\ell_0$-regularization path, which is piecewise constant with respect to $\lambda$. Both algorithms are empirically evaluated for difficult inverse problems involving ill-conditioned dictionaries. Finally, we show that they can be easily coupled with usual methods of model order selection.

Algorithms for nonnegative matrix factorization with the beta-divergence

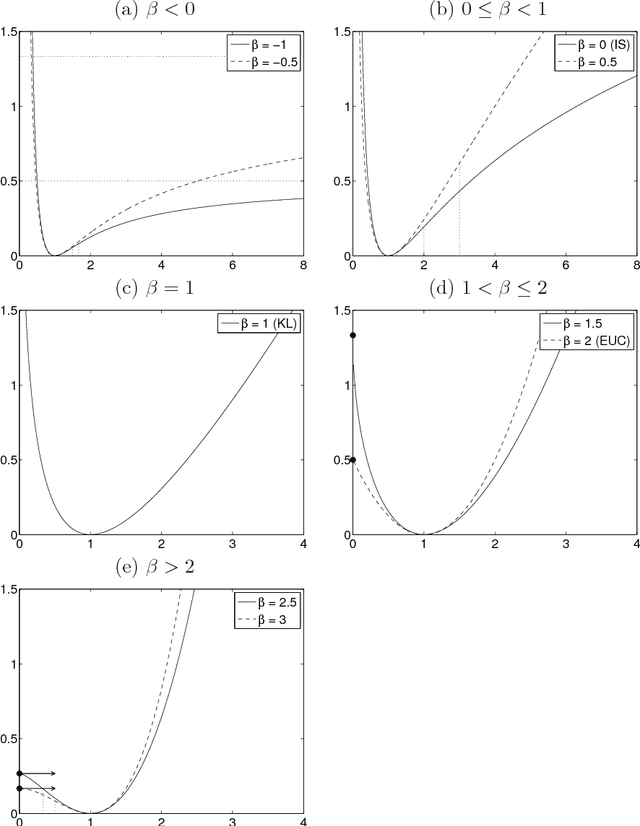
This paper describes algorithms for nonnegative matrix factorization (NMF) with the beta-divergence (beta-NMF). The beta-divergence is a family of cost functions parametrized by a single shape parameter beta that takes the Euclidean distance, the Kullback-Leibler divergence and the Itakura-Saito divergence as special cases (beta = 2,1,0, respectively). The proposed algorithms are based on a surrogate auxiliary function (a local majorization of the criterion function). We first describe a majorization-minimization (MM) algorithm that leads to multiplicative updates, which differ from standard heuristic multiplicative updates by a beta-dependent power exponent. The monotonicity of the heuristic algorithm can however be proven for beta in (0,1) using the proposed auxiliary function. Then we introduce the concept of majorization-equalization (ME) algorithm which produces updates that move along constant level sets of the auxiliary function and lead to larger steps than MM. Simulations on synthetic and real data illustrate the faster convergence of the ME approach. The paper also describes how the proposed algorithms can be adapted to two common variants of NMF : penalized NMF (i.e., when a penalty function of the factors is added to the criterion function) and convex-NMF (when the dictionary is assumed to belong to a known subspace).