Cédric Févotte
IRIT-SC, CNRS
Audio signal interpolation using optimal transportation of spectrograms
Feb 21, 2025Abstract:We present a novel approach for generating an artificial audio signal that interpolates between given source and target sounds. Our approach relies on the computation of Wasserstein barycenters of the source and target spectrograms, followed by phase reconstruction and inversion. In contrast with previous works, our new method considers the spectrograms globally and does not operate on a temporal frame-to-frame basis. An other contribution is to endow the transportation cost matrix with a specific structure that prohibits remote displacements of energy along the time axis, and for which optimal transport is made possible by leveraging the unbalanced transport framework. The proposed cost matrix makes sense from the audio perspective and also allows to reduce the computation load. Results with synthetic musical notes and real environmental sounds illustrate the potential of our novel approach.
Majorization-minimization for Sparse Nonnegative Matrix Factorization with the $β$-divergence
Jul 13, 2022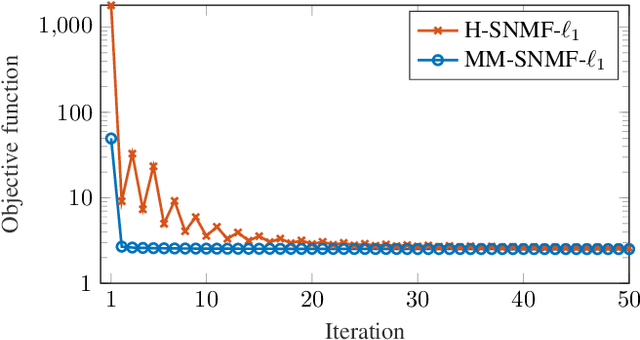
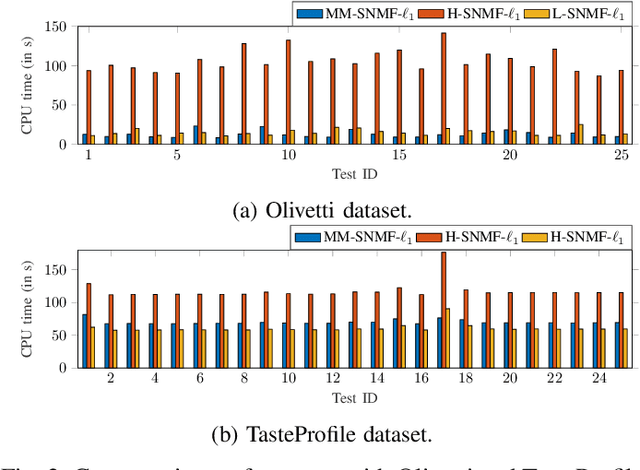
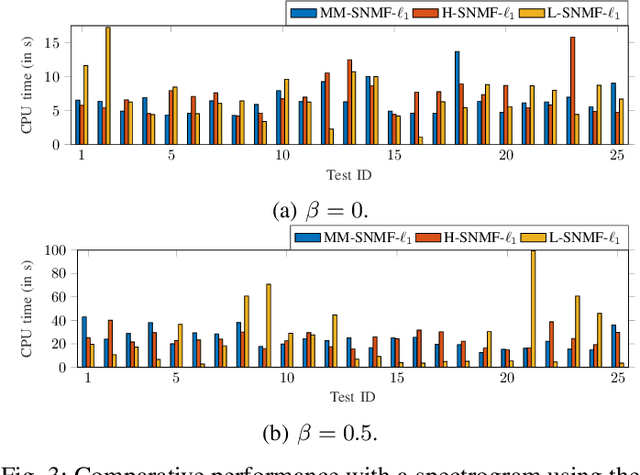
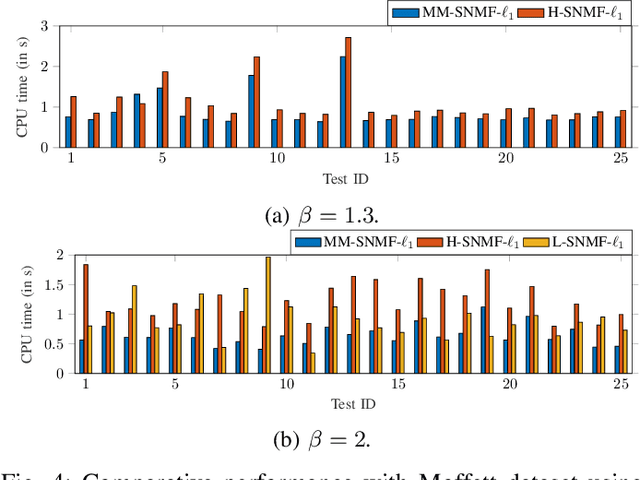
Abstract:This article introduces new multiplicative updates for nonnegative matrix factorization with the $\beta$-divergence and sparse regularization of one of the two factors (say, the activation matrix). It is well known that the norm of the other factor (the dictionary matrix) needs to be controlled in order to avoid an ill-posed formulation. Standard practice consists in constraining the columns of the dictionary to have unit norm, which leads to a nontrivial optimization problem. Our approach leverages a reparametrization of the original problem into the optimization of an equivalent scale-invariant objective function. From there, we derive block-descent majorization-minimization algorithms that result in simple multiplicative updates for either $\ell_{1}$-regularization or the more "aggressive" log-regularization. In contrast with other state-of-the-art methods, our algorithms are universal in the sense that they can be applied to any $\beta$-divergence (i.e., any value of $\beta$) and that they come with convergence guarantees. We report numerical comparisons with existing heuristic and Lagrangian methods using various datasets: face images, an audio spectrogram, hyperspectral data, and song play counts. We show that our methods obtain solutions of similar quality at convergence (similar objective values) but with significantly reduced CPU times.
Algorithms for audio inpainting based on probabilistic nonnegative matrix factorization
Jun 28, 2022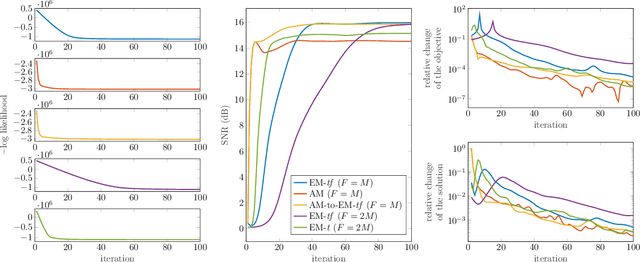

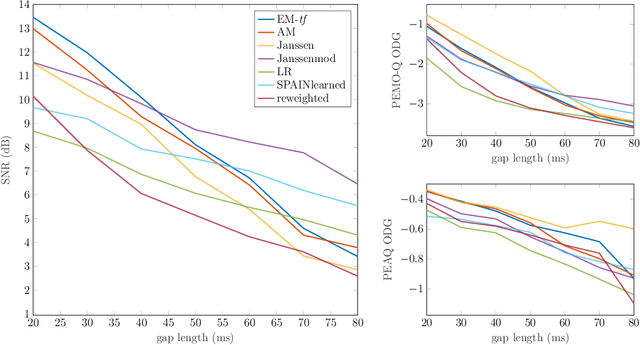
Abstract:Audio inpainting, i.e., the task of restoring missing or occluded audio signal samples, usually relies on sparse representations or autoregressive modeling. In this paper, we propose to structure the spectrogram with nonnegative matrix factorization (NMF) in a probabilistic framework. First, we treat the missing samples as latent variables, and derive two expectation-maximization algorithms for estimating the parameters of the model, depending on whether we formulate the problem in the time- or time-frequency domain. Then, we treat the missing samples as parameters, and we address this novel problem by deriving an alternating minimization scheme. We assess the potential of these algorithms for the task of restoring short- to middle-length gaps in music signals. Experiments reveal great convergence properties of the proposed methods, as well as competitive performance when compared to state-of-the-art audio inpainting techniques.
A majorization-minimization algorithm for nonnegative binary matrix factorization
Apr 20, 2022
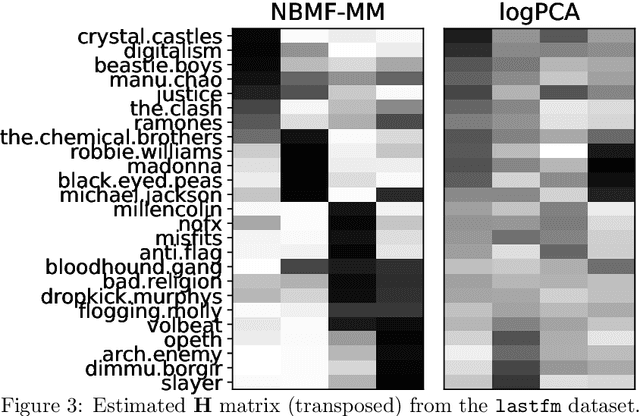
Abstract:This paper tackles the problem of decomposing binary data using matrix factorization. We consider the family of mean-parametrized Bernoulli models, a class of generative models that are well suited for modeling binary data and enables interpretability of the factors. We factorize the Bernoulli parameter and consider an additional Beta prior on one of the factors to further improve the model's expressive power. While similar models have been proposed in the literature, they only exploit the Beta prior as a proxy to ensure a valid Bernoulli parameter in a Bayesian setting; in practice it reduces to a uniform or uninformative prior. Besides, estimation in these models has focused on costly Bayesian inference. In this paper, we propose a simple yet very efficient majorization-minimization algorithm for maximum a posteriori estimation. Our approach leverages the Beta prior whose parameters can be tuned to improve performance in matrix completion tasks. Experiments conducted on three public binary datasets show that our approach offers an excellent trade-off between prediction performance, computational complexity, and interpretability.
Learning the Proximity Operator in Unfolded ADMM for Phase Retrieval
Apr 04, 2022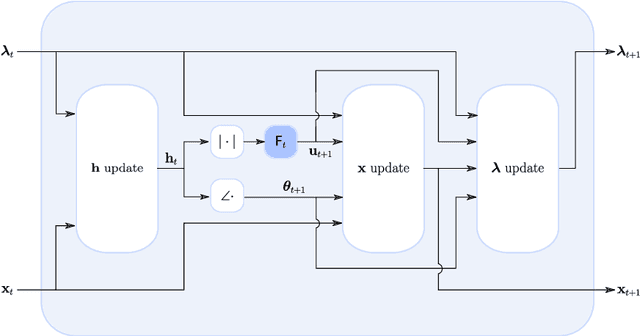
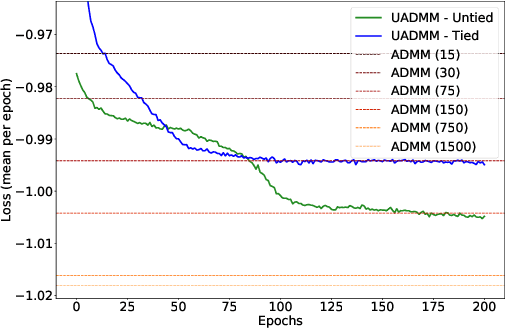
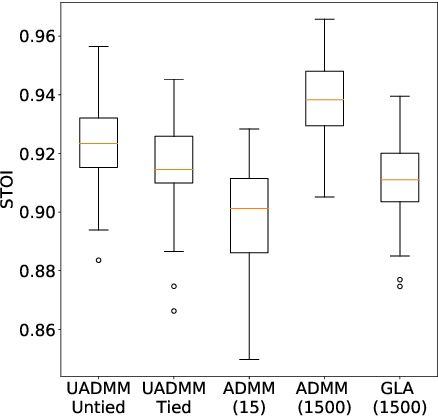
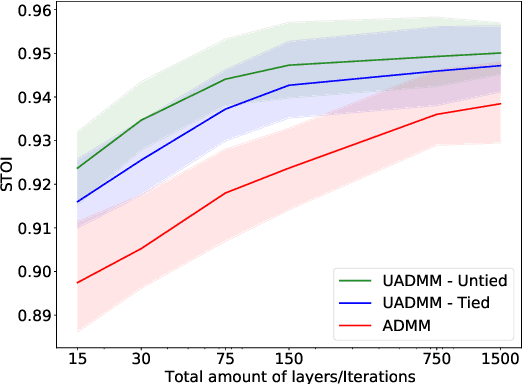
Abstract:This paper considers the phase retrieval (PR) problem, which aims to reconstruct a signal from phaseless measurements such as magnitude or power spectrograms. PR is generally handled as a minimization problem involving a quadratic loss. Recent works have considered alternative discrepancy measures, such as the Bregman divergences, but it is still challenging to tailor the optimal loss for a given setting. In this paper we propose a novel strategy to automatically learn the optimal metric for PR. We unfold a recently introduced ADMM algorithm into a neural network, and we emphasize that the information about the loss used to formulate the PR problem is conveyed by the proximity operator involved in the ADMM updates. Therefore, we replace this proximity operator with trainable activation functions: learning these in a supervised setting is then equivalent to learning an optimal metric for PR. Experiments conducted with speech signals show that our approach outperforms the baseline ADMM, using a light and interpretable neural architecture.
Accelerating Non-Negative and Bounded-Variable Linear Regression Algorithms with Safe Screening
Feb 15, 2022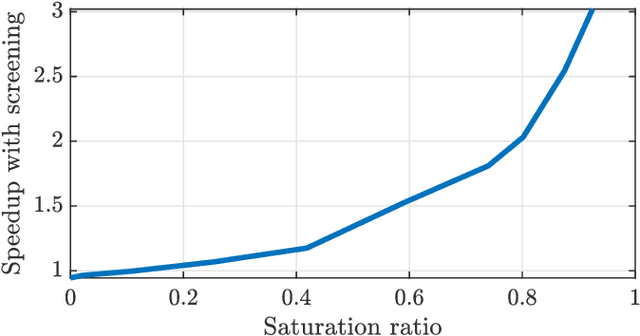
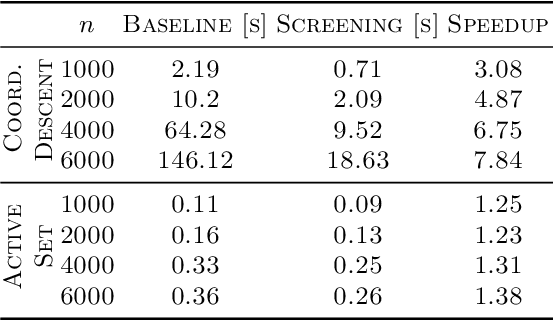
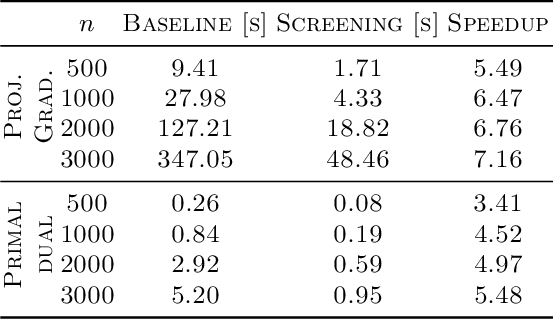
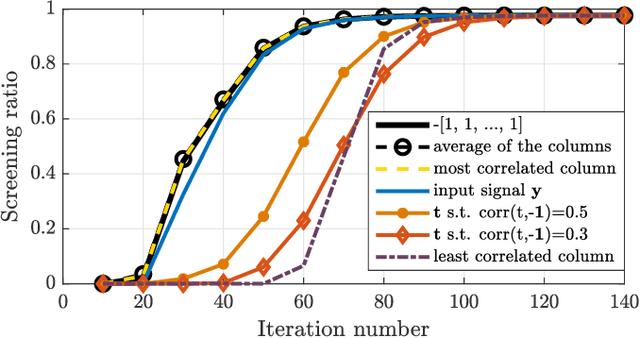
Abstract:Non-negative and bounded-variable linear regression problems arise in a variety of applications in machine learning and signal processing. In this paper, we propose a technique to accelerate existing solvers for these problems by identifying saturated coordinates in the course of iterations. This is akin to safe screening techniques previously proposed for sparsity-regularized regression problems. The proposed strategy is provably safe as it provides theoretical guarantees that the identified coordinates are indeed saturated in the optimal solution. Experimental results on synthetic and real data show compelling accelerations for both non-negative and bounded-variable problems.
On the Relationships between Transform-Learning NMF and Joint-Diagonalization
Dec 10, 2021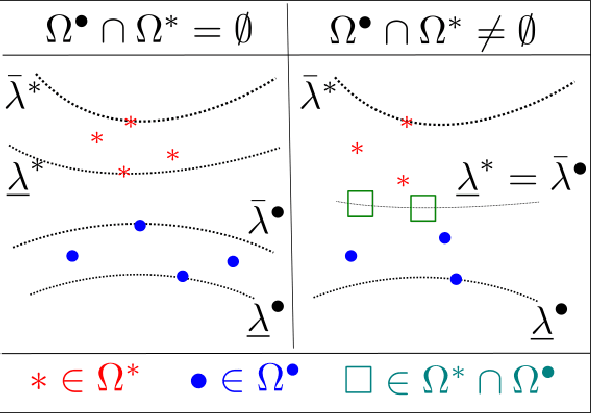
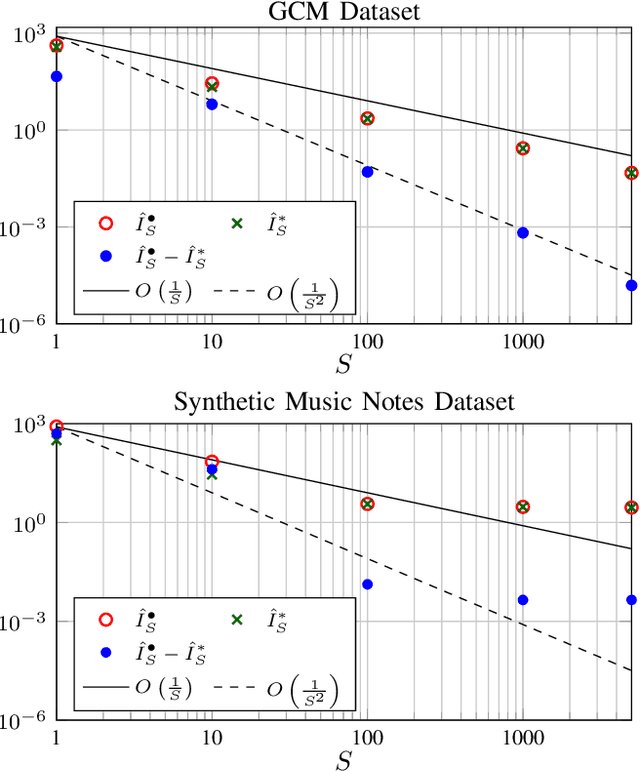
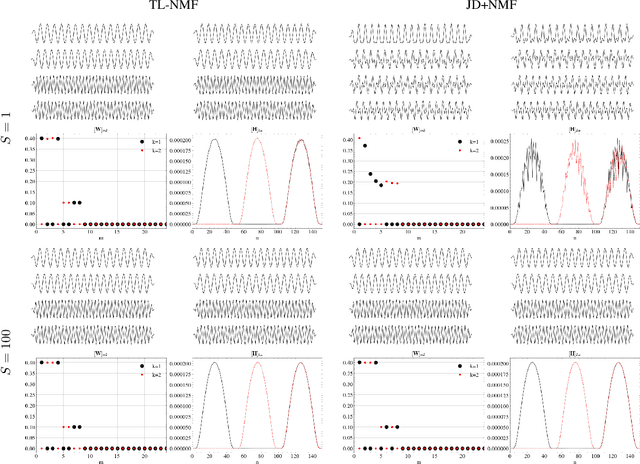
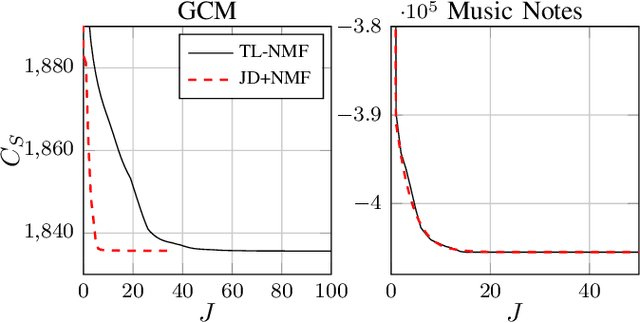
Abstract:Non-negative matrix factorization with transform learning (TL-NMF) is a recent idea that aims at learning data representations suited to NMF. In this work, we relate TL-NMF to the classical matrix joint-diagonalization (JD) problem. We show that, when the number of data realizations is sufficiently large, TL-NMF can be replaced by a two-step approach -- termed as JD+NMF -- that estimates the transform through JD, prior to NMF computation. In contrast, we found that when the number of data realizations is limited, not only is JD+NMF no longer equivalent to TL-NMF, but the inherent low-rank constraint of TL-NMF turns out to be an essential ingredient to learn meaningful transforms for NMF.
Joint Majorization-Minimization for Nonnegative Matrix Factorization with the $β$-divergence
Jun 29, 2021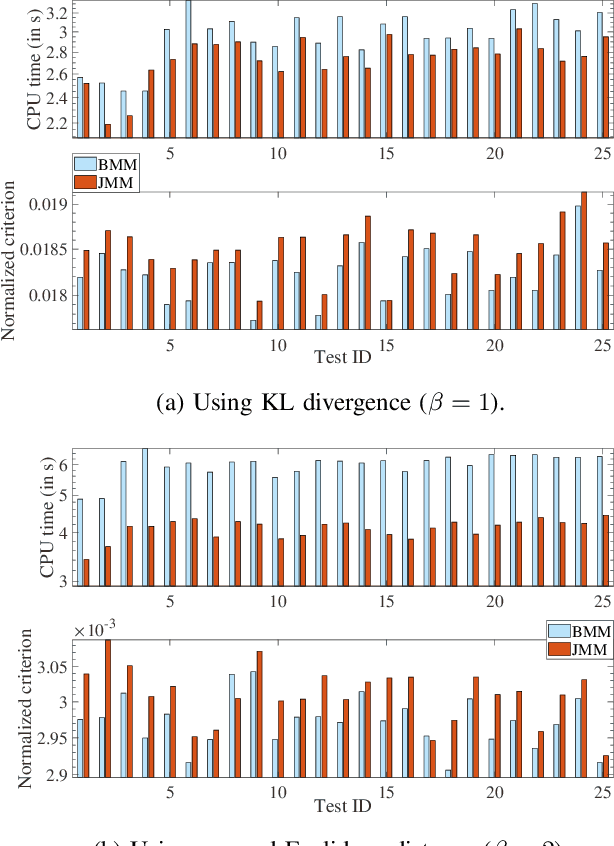
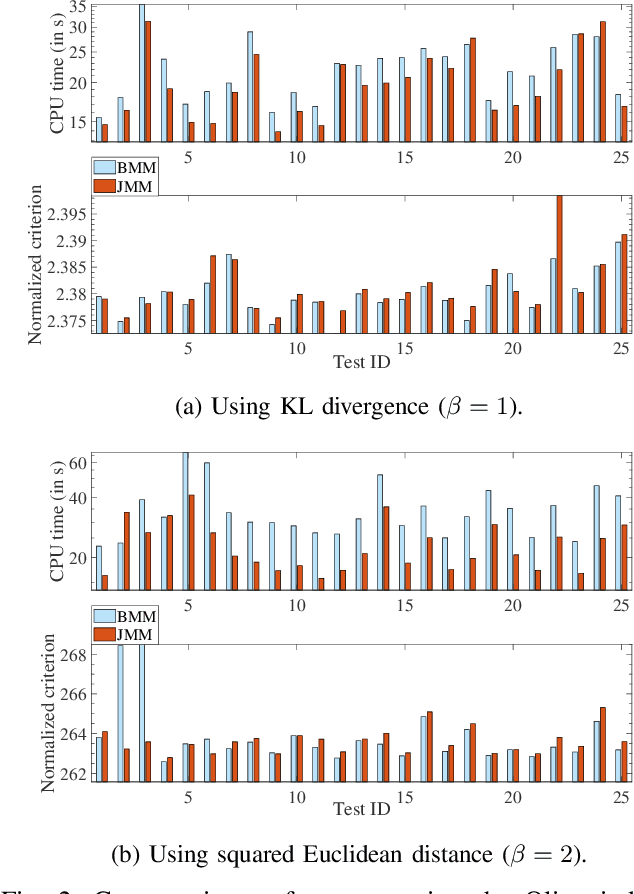
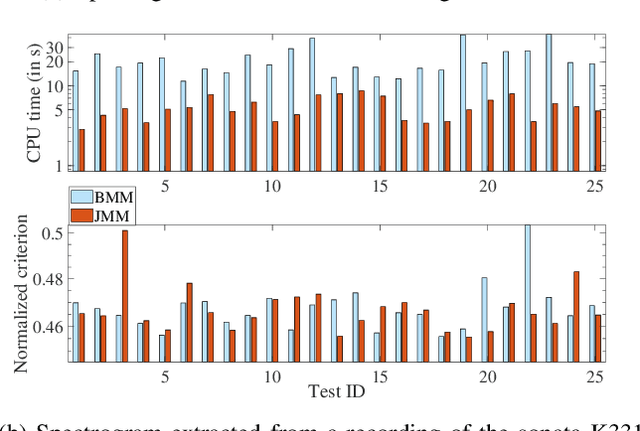
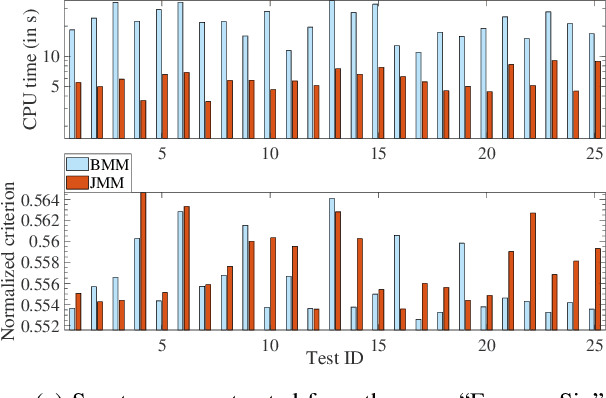
Abstract:This article proposes new multiplicative updates for nonnegative matrix factorization (NMF) with the $\beta$-divergence objective function. Our new updates are derived from a joint majorization-minimization (MM) scheme, in which an auxiliary function (a tight upper bound of the objective function) is built for the two factors jointly and minimized at each iteration. This is in contrast with the classic approach in which the factors are optimized alternately and a MM scheme is applied to each factor individually. Like the classic approach, our joint MM algorithm also results in multiplicative updates that are simple to implement. They however yield a significant drop of computation time (for equally good solutions), in particular for some $\beta$-divergences of important applicative interest, such as the squared Euclidean distance and the Kullback-Leibler or Itakura-Saito divergences. We report experimental results using diverse datasets: face images, audio spectrograms, hyperspectral data and song play counts. Depending on the value of $\beta$ and on the dataset, our joint MM approach yields a CPU time reduction of about $10\%$ to $78\%$ in comparison to the classic alternating scheme.
Unbalanced Optimal Transport through Non-negative Penalized Linear Regression
Jun 08, 2021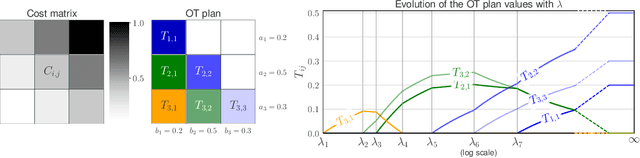
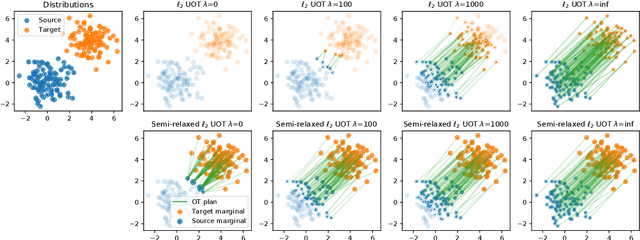
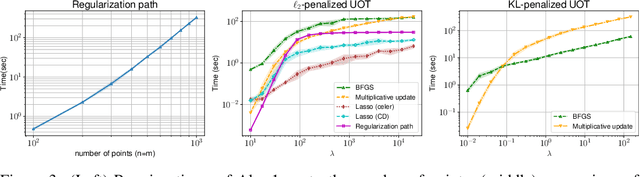
Abstract:This paper addresses the problem of Unbalanced Optimal Transport (UOT) in which the marginal conditions are relaxed (using weighted penalties in lieu of equality) and no additional regularization is enforced on the OT plan. In this context, we show that the corresponding optimization problem can be reformulated as a non-negative penalized linear regression problem. This reformulation allows us to propose novel algorithms inspired from inverse problems and nonnegative matrix factorization. In particular, we consider majorization-minimization which leads in our setting to efficient multiplicative updates for a variety of penalties. Furthermore, we derive for the first time an efficient algorithm to compute the regularization path of UOT with quadratic penalties. The proposed algorithm provides a continuity of piece-wise linear OT plans converging to the solution of balanced OT (corresponding to infinite penalty weights). We perform several numerical experiments on simulated and real data illustrating the new algorithms, and provide a detailed discussion about more sophisticated optimization tools that can further be used to solve OT problems thanks to our reformulation.
Adversarially-Trained Nonnegative Matrix Factorization
Apr 10, 2021
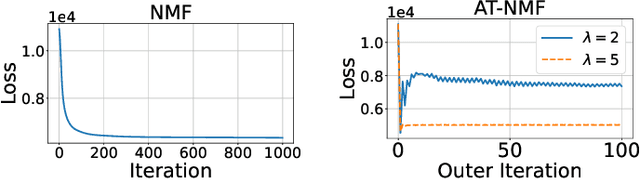


Abstract:We consider an adversarially-trained version of the nonnegative matrix factorization, a popular latent dimensionality reduction technique. In our formulation, an attacker adds an arbitrary matrix of bounded norm to the given data matrix. We design efficient algorithms inspired by adversarial training to optimize for dictionary and coefficient matrices with enhanced generalization abilities. Extensive simulations on synthetic and benchmark datasets demonstrate the superior predictive performance on matrix completion tasks of our proposed method compared to state-of-the-art competitors, including other variants of adversarial nonnegative matrix factorization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge