Pierre-Hugo Vial
Learning the Proximity Operator in Unfolded ADMM for Phase Retrieval
Apr 04, 2022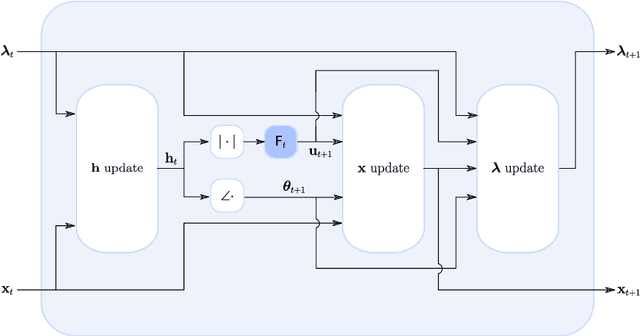
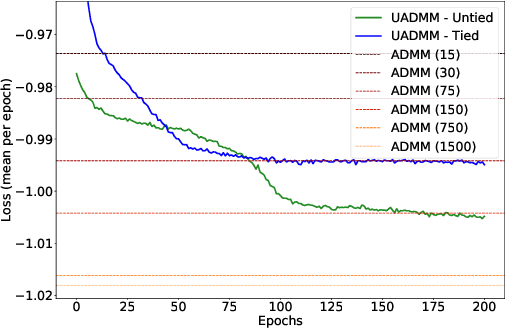
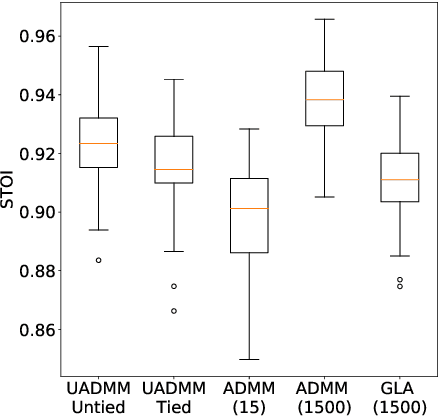
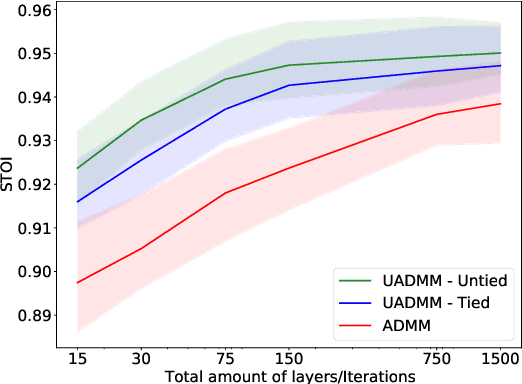
Abstract:This paper considers the phase retrieval (PR) problem, which aims to reconstruct a signal from phaseless measurements such as magnitude or power spectrograms. PR is generally handled as a minimization problem involving a quadratic loss. Recent works have considered alternative discrepancy measures, such as the Bregman divergences, but it is still challenging to tailor the optimal loss for a given setting. In this paper we propose a novel strategy to automatically learn the optimal metric for PR. We unfold a recently introduced ADMM algorithm into a neural network, and we emphasize that the information about the loss used to formulate the PR problem is conveyed by the proximity operator involved in the ADMM updates. Therefore, we replace this proximity operator with trainable activation functions: learning these in a supervised setting is then equivalent to learning an optimal metric for PR. Experiments conducted with speech signals show that our approach outperforms the baseline ADMM, using a light and interpretable neural architecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge