Automated transport separation using the neural shifted proper orthogonal decomposition

This paper presents a neural network-based methodology for the decomposition of transport-dominated fields using the shifted proper orthogonal decomposition (sPOD). Classical sPOD methods typically require an a priori knowledge of the transport operators to determine the co-moving fields. However, in many real-life problems, such knowledge is difficult or even impossible to obtain, limiting the applicability and benefits of the sPOD. To address this issue, our approach estimates both the transport and co-moving fields simultaneously using neural networks. This is achieved by training two sub-networks dedicated to learning the transports and the co-moving fields, respectively. Applications to synthetic data and a wildland fire model illustrate the capabilities and efficiency of this neural sPOD approach, demonstrating its ability to separate the different fields effectively.

Majorization-minimization for Sparse Nonnegative Matrix Factorization with the $β$-divergence

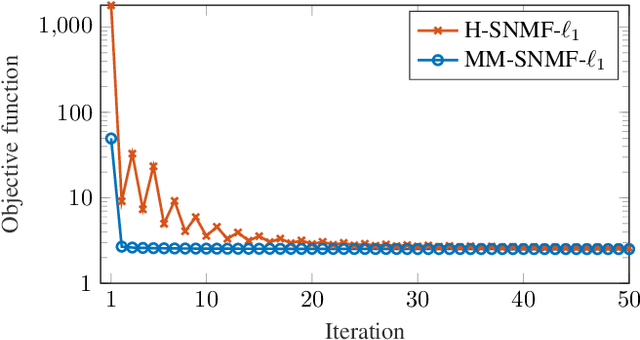
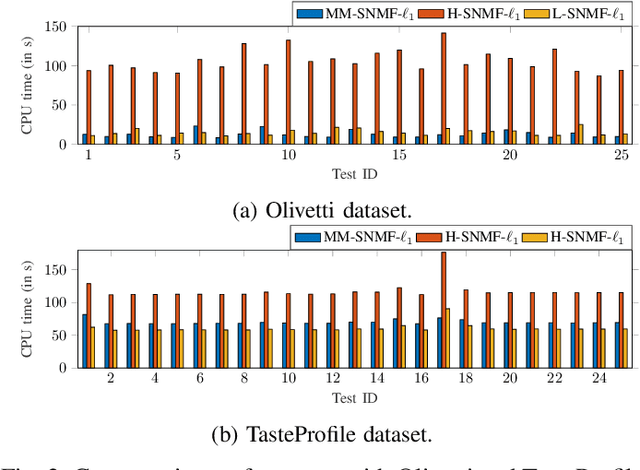
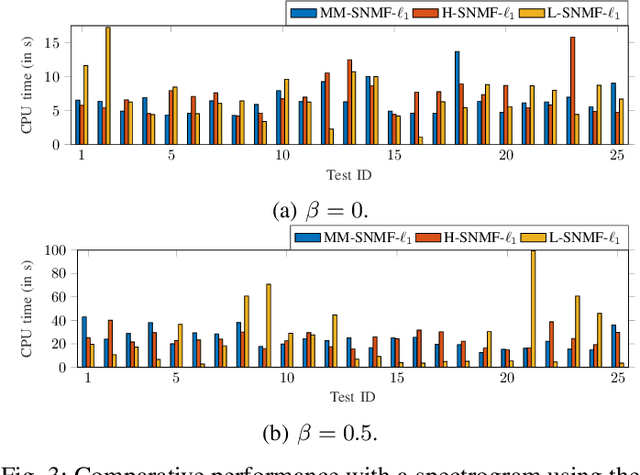
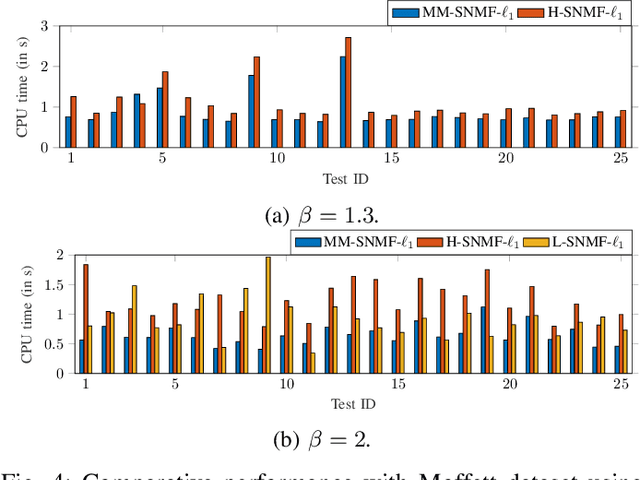
This article introduces new multiplicative updates for nonnegative matrix factorization with the $\beta$-divergence and sparse regularization of one of the two factors (say, the activation matrix). It is well known that the norm of the other factor (the dictionary matrix) needs to be controlled in order to avoid an ill-posed formulation. Standard practice consists in constraining the columns of the dictionary to have unit norm, which leads to a nontrivial optimization problem. Our approach leverages a reparametrization of the original problem into the optimization of an equivalent scale-invariant objective function. From there, we derive block-descent majorization-minimization algorithms that result in simple multiplicative updates for either $\ell_{1}$-regularization or the more "aggressive" log-regularization. In contrast with other state-of-the-art methods, our algorithms are universal in the sense that they can be applied to any $\beta$-divergence (i.e., any value of $\beta$) and that they come with convergence guarantees. We report numerical comparisons with existing heuristic and Lagrangian methods using various datasets: face images, an audio spectrogram, hyperspectral data, and song play counts. We show that our methods obtain solutions of similar quality at convergence (similar objective values) but with significantly reduced CPU times.

Joint Majorization-Minimization for Nonnegative Matrix Factorization with the $β$-divergence

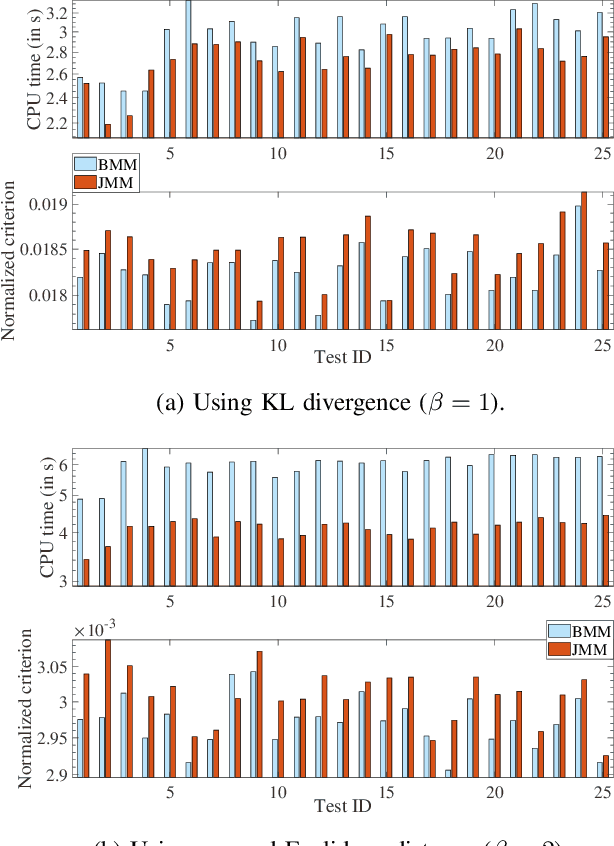
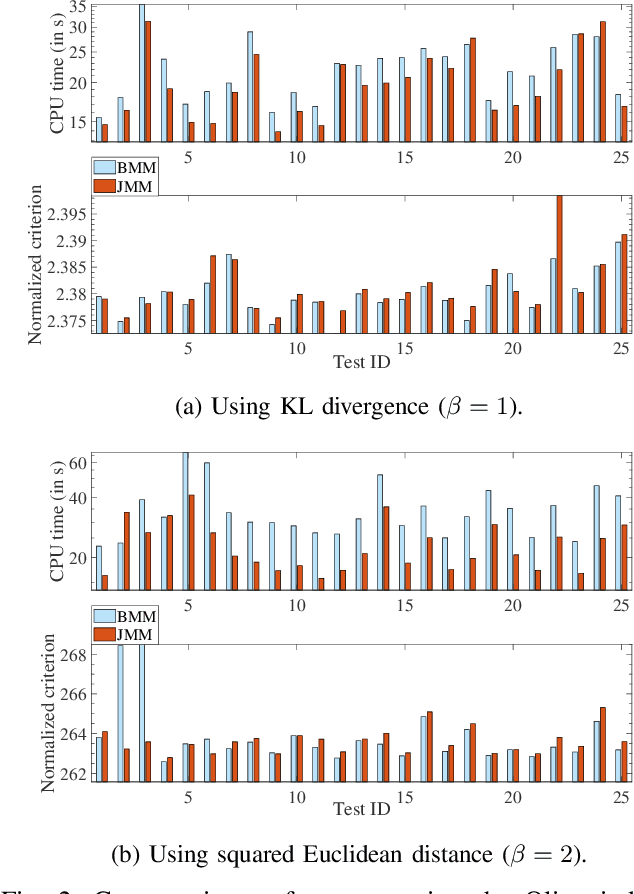
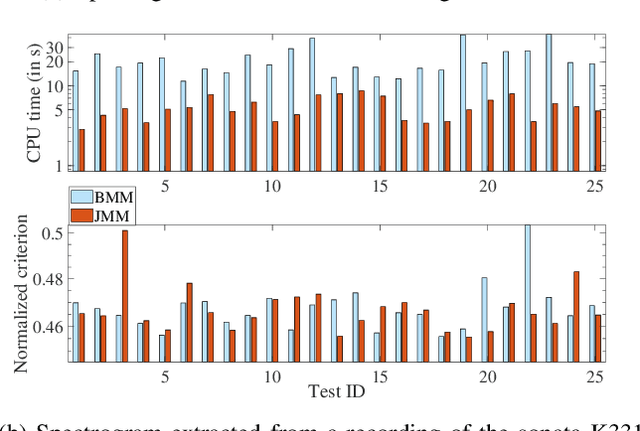
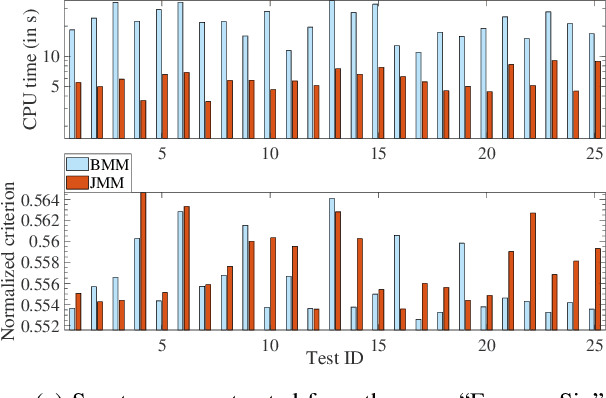
This article proposes new multiplicative updates for nonnegative matrix factorization (NMF) with the $\beta$-divergence objective function. Our new updates are derived from a joint majorization-minimization (MM) scheme, in which an auxiliary function (a tight upper bound of the objective function) is built for the two factors jointly and minimized at each iteration. This is in contrast with the classic approach in which the factors are optimized alternately and a MM scheme is applied to each factor individually. Like the classic approach, our joint MM algorithm also results in multiplicative updates that are simple to implement. They however yield a significant drop of computation time (for equally good solutions), in particular for some $\beta$-divergences of important applicative interest, such as the squared Euclidean distance and the Kullback-Leibler or Itakura-Saito divergences. We report experimental results using diverse datasets: face images, audio spectrograms, hyperspectral data and song play counts. Depending on the value of $\beta$ and on the dataset, our joint MM approach yields a CPU time reduction of about $10\%$ to $78\%$ in comparison to the classic alternating scheme.

Sparse Signal Reconstruction for Nonlinear Models via Piecewise Rational Optimization

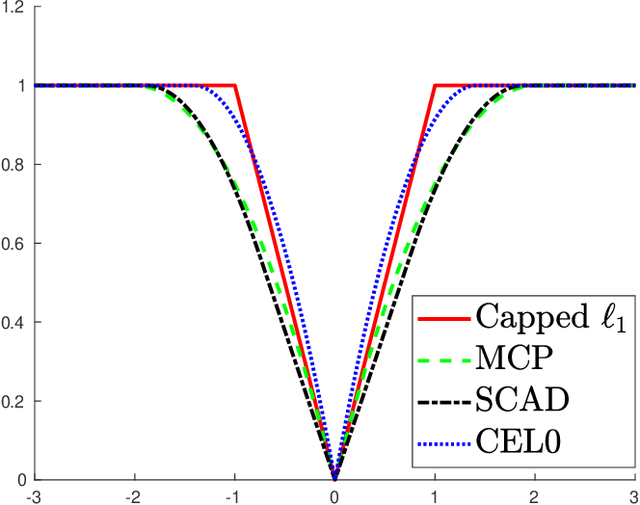
We propose a method to reconstruct sparse signals degraded by a nonlinear distortion and acquired at a limited sampling rate. Our method formulates the reconstruction problem as a nonconvex minimization of the sum of a data fitting term and a penalization term. In contrast with most previous works which settle for approximated local solutions, we seek for a global solution to the obtained challenging nonconvex problem. Our global approach relies on the so-called Lasserre relaxation of polynomial optimization. We here specifically include in our approach the case of piecewise rational functions, which makes it possible to address a wide class of nonconvex exact and continuous relaxations of the $\ell_0$ penalization function. Additionally, we study the complexity of the optimization problem. It is shown how to use the structure of the problem to lighten the computational burden efficiently. Finally, numerical simulations illustrate the benefits of our method in terms of both global optimality and signal reconstruction.