Démélange, déconvolution et débruitage conjoints d'un modèle convolutif parcimonieux avec dérive instrumentale, par pénalisation de rapports de normes ou quasi-normes lissées (PENDANTSS)

Denoising, detrending, deconvolution: usual restoration tasks, traditionally decoupled. Coupled formulations entail complex ill-posed inverse problems. We propose PENDANTSS for joint trend removal and blind deconvolution of sparse peak-like signals. It blends a parsimonious prior with the hypothesis that smooth trend and noise can somewhat be separated by low-pass filtering. We combine the generalized pseudo-norm ratio SOOT/SPOQ sparse penalties $\ell_p/\ell_q$ with the BEADS ternary assisted source separation algorithm. This results in a both convergent and efficient tool, with a novel Trust-Region block alternating variable metric forward-backward approach. It outperforms comparable methods, when applied to typically peaked analytical chemistry signals. Reproducible code is provided: https://github.com/paulzhengfr/PENDANTSS.

Dual-sPLS: a family of Dual Sparse Partial Least Squares regressions for feature selection and prediction with tunable sparsity; evaluation on simulated and near-infrared data

Relating a set of variables X to a response y is crucial in chemometrics. A quantitative prediction objective can be enriched by qualitative data interpretation, for instance by locating the most influential features. When high-dimensional problems arise, dimension reduction techniques can be used. Most notable are projections (e.g. Partial Least Squares or PLS ) or variable selections (e.g. lasso). Sparse partial least squares combine both strategies, by blending variable selection into PLS. The variant presented in this paper, Dual-sPLS, generalizes the classical PLS1 algorithm. It provides balance between accurate prediction and efficient interpretation. It is based on penalizations inspired by classical regression methods (lasso, group lasso, least squares, ridge) and uses the dual norm notion. The resulting sparsity is enforced by an intuitive shrinking ratio parameter. Dual-sPLS favorably compares to similar regression methods, on simulated and real chemical data. Code is provided as an open-source package in R: \url{https://CRAN.R-project.org/package=dual.spls}.

PENDANTSS: PEnalized Norm-ratios Disentangling Additive Noise, Trend and Sparse Spikes

Denoising, detrending, deconvolution: usual restoration tasks, traditionally decoupled. Coupled formulations entail complex ill-posed inverse problems. We propose PENDANTSS for joint trend removal and blind deconvolution of sparse peak-like signals. It blends a parsimonious prior with the hypothesis that smooth trend and noise can somewhat be separated by low-pass filtering. We combine the generalized quasi-norm ratio SOOT/SPOQ sparse penalties $\ell_p/\ell_q$ with the BEADS ternary assisted source separation algorithm. This results in a both convergent and efficient tool, with a novel Trust-Region block alternating variable metric forward-backward approach. It outperforms comparable methods, when applied to typically peaked analytical chemistry signals. Reproducible code is provided.

Sparse Signal Reconstruction for Nonlinear Models via Piecewise Rational Optimization

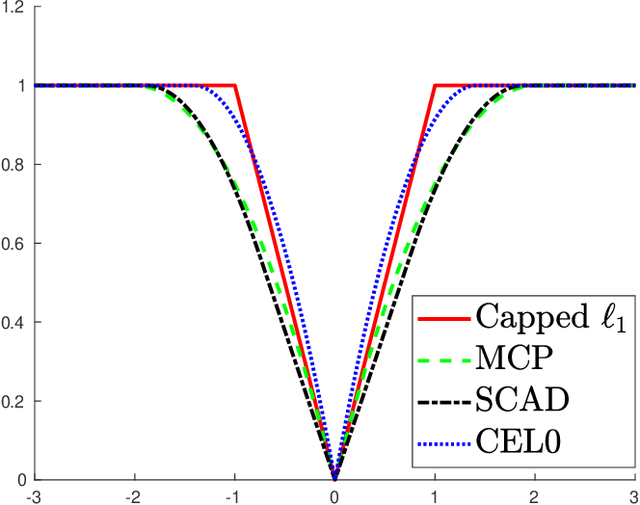
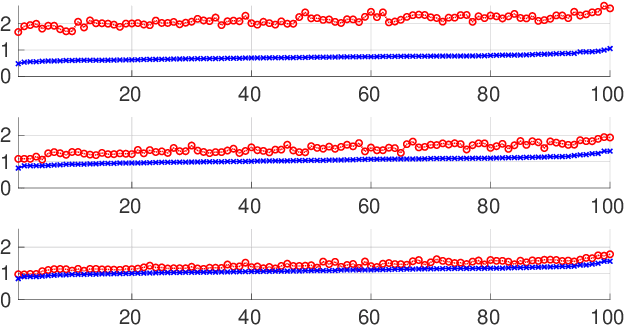
We propose a method to reconstruct sparse signals degraded by a nonlinear distortion and acquired at a limited sampling rate. Our method formulates the reconstruction problem as a nonconvex minimization of the sum of a data fitting term and a penalization term. In contrast with most previous works which settle for approximated local solutions, we seek for a global solution to the obtained challenging nonconvex problem. Our global approach relies on the so-called Lasserre relaxation of polynomial optimization. We here specifically include in our approach the case of piecewise rational functions, which makes it possible to address a wide class of nonconvex exact and continuous relaxations of the $\ell_0$ penalization function. Additionally, we study the complexity of the optimization problem. It is shown how to use the structure of the problem to lighten the computational burden efficiently. Finally, numerical simulations illustrate the benefits of our method in terms of both global optimality and signal reconstruction.

HexaShrink, an exact scalable framework for hexahedral meshes with attributes and discontinuities: multiresolution rendering and storage of geoscience models

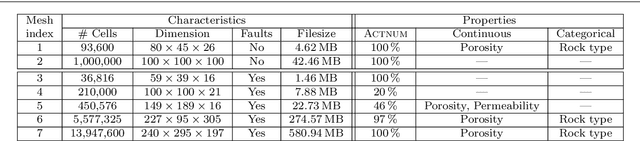
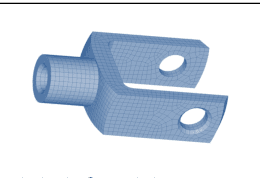
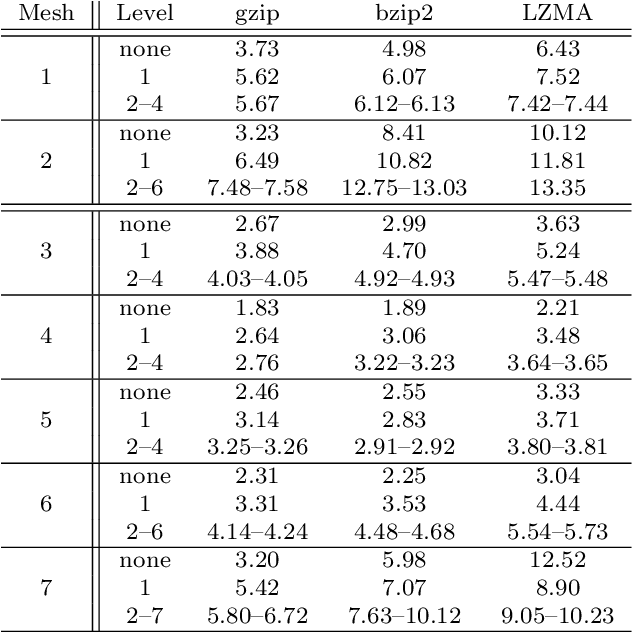
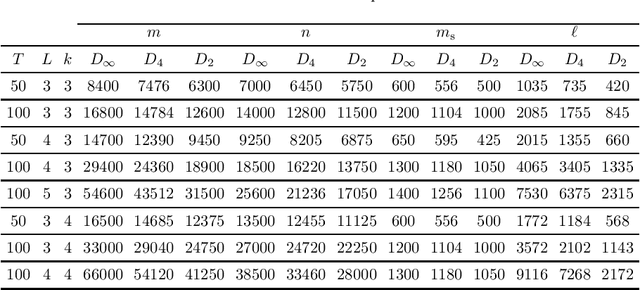
With huge data acquisition progresses realized in the past decades and acquisition systems now able to produce high resolution grids and point clouds, the digitization of physical terrains becomes increasingly more precise. Such extreme quantities of generated and modeled data greatly impact computational performances on many levels of high-performance computing (HPC): storage media, memory requirements, transfer capability, and finally simulation interactivity, necessary to exploit this instance of big data. Efficient representations and storage are thus becoming "enabling technologies'' in HPC experimental and simulation science. We propose HexaShrink, an original decomposition scheme for structured hexahedral volume meshes. The latter are used for instance in biomedical engineering, materials science, or geosciences. HexaShrink provides a comprehensive framework allowing efficient mesh visualization and storage. Its exactly reversible multiresolution decomposition yields a hierarchy of meshes of increasing levels of details, in terms of either geometry, continuous or categorical properties of cells. Starting with an overview of volume meshes compression techniques, our contribution blends coherently different multiresolution wavelet schemes in different dimensions. It results in a global framework preserving discontinuities (faults) across scales, implemented as a fully reversible upscaling at different resolutions. Experimental results are provided on meshes of varying size and complexity. They emphasize the consistency of the proposed representation, in terms of visualization, attribute downsampling and distribution at different resolutions. Finally, HexaShrink yields gains in storage space when combined to lossless compression techniques.

Image Analysis Using a Dual-Tree $M$-Band Wavelet Transform

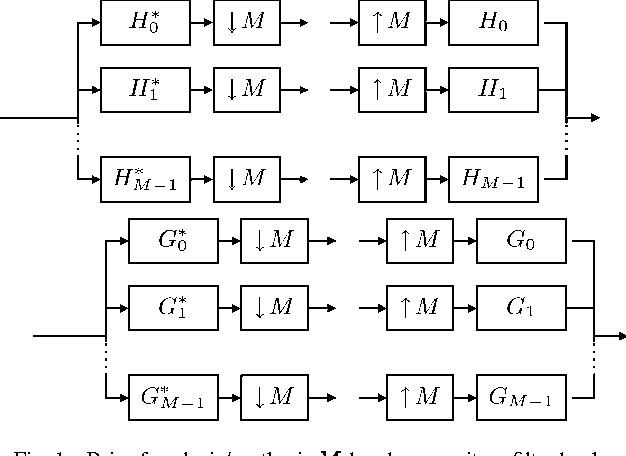
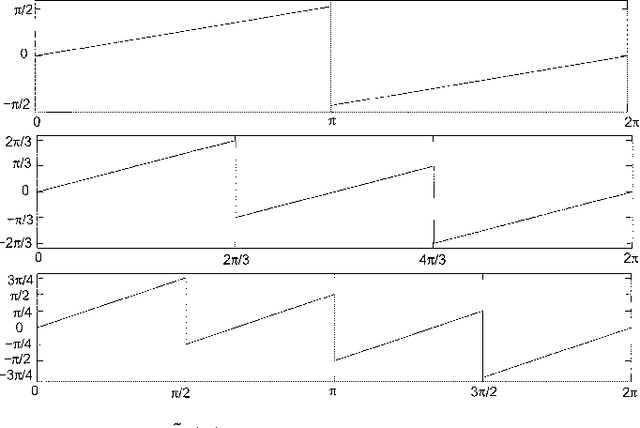
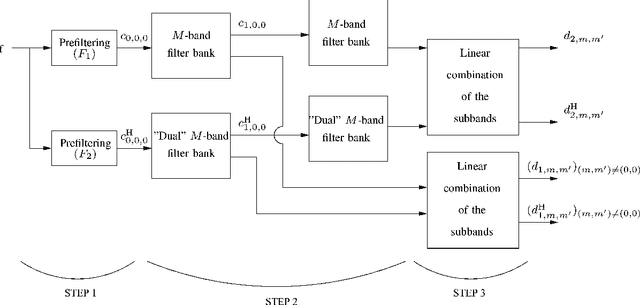
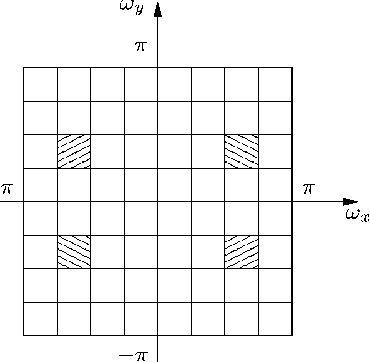
We propose a 2D generalization to the $M$-band case of the dual-tree decomposition structure (initially proposed by N. Kingsbury and further investigated by I. Selesnick) based on a Hilbert pair of wavelets. We particularly address (\textit{i}) the construction of the dual basis and (\textit{ii}) the resulting directional analysis. We also revisit the necessary pre-processing stage in the $M$-band case. While several reconstructions are possible because of the redundancy of the representation, we propose a new optimal signal reconstruction technique, which minimizes potential estimation errors. The effectiveness of the proposed $M$-band decomposition is demonstrated via denoising comparisons on several image types (natural, texture, seismics), with various $M$-band wavelets and thresholding strategies. Significant improvements in terms of both overall noise reduction and direction preservation are observed.

BARCHAN: Blob Alignment for Robust CHromatographic ANalysis

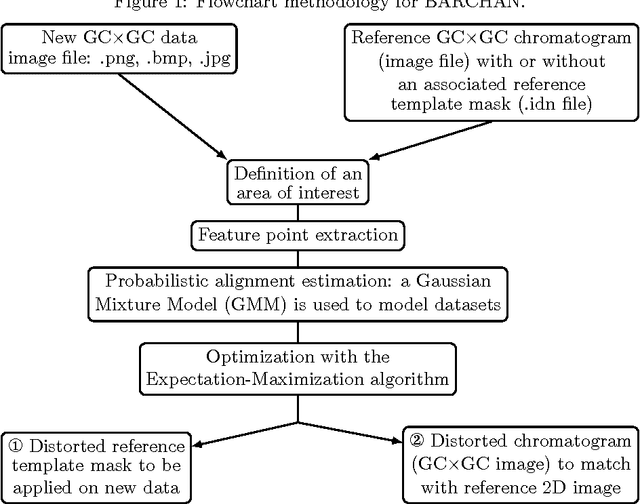
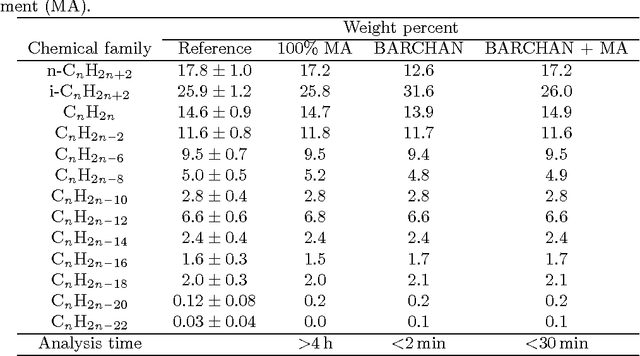
Comprehensive Two dimensional gas chromatography (GCxGC) plays a central role into the elucidation of complex samples. The automation of the identification of peak areas is of prime interest to obtain a fast and repeatable analysis of chromatograms. To determine the concentration of compounds or pseudo-compounds, templates of blobs are defined and superimposed on a reference chromatogram. The templates then need to be modified when different chromatograms are recorded. In this study, we present a chromatogram and template alignment method based on peak registration called BARCHAN. Peaks are identified using a robust mathematical morphology tool. The alignment is performed by a probabilistic estimation of a rigid transformation along the first dimension, and a non-rigid transformation in the second dimension, taking into account noise, outliers and missing peaks in a fully automated way. Resulting aligned chromatograms and masks are presented on two datasets. The proposed algorithm proves to be fast and reliable. It significantly reduces the time to results for GCxGC analysis.

Noise Covariance Properties in Dual-Tree Wavelet Decompositions

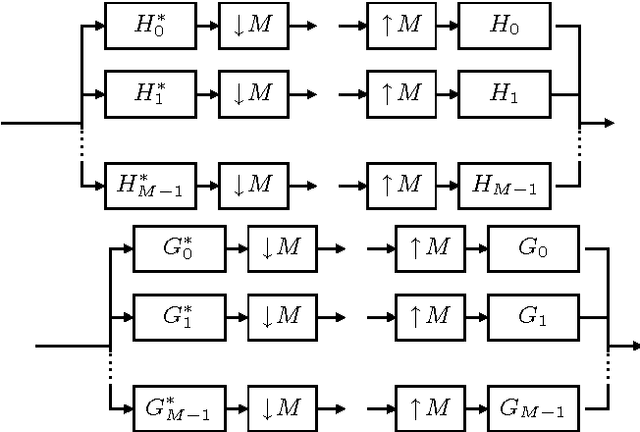
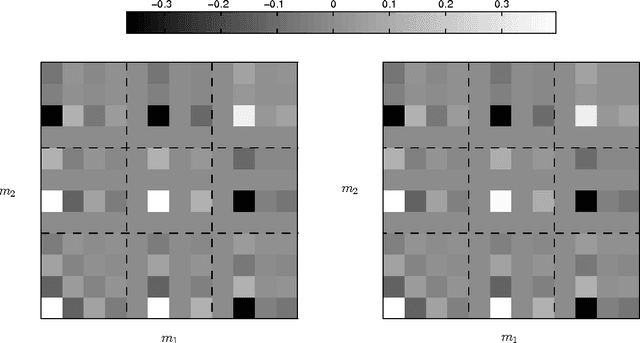
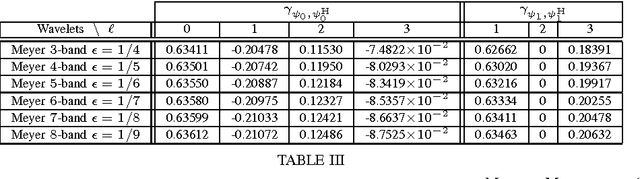
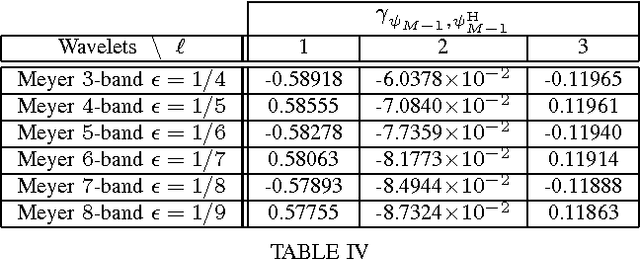
Dual-tree wavelet decompositions have recently gained much popularity, mainly due to their ability to provide an accurate directional analysis of images combined with a reduced redundancy. When the decomposition of a random process is performed -- which occurs in particular when an additive noise is corrupting the signal to be analyzed -- it is useful to characterize the statistical properties of the dual-tree wavelet coefficients of this process. As dual-tree decompositions constitute overcomplete frame expansions, correlation structures are introduced among the coefficients, even when a white noise is analyzed. In this paper, we show that it is possible to provide an accurate description of the covariance properties of the dual-tree coefficients of a wide-sense stationary process. The expressions of the (cross-)covariance sequences of the coefficients are derived in the one and two-dimensional cases. Asymptotic results are also provided, allowing to predict the behaviour of the second-order moments for large lag values or at coarse resolution. In addition, the cross-correlations between the primal and dual wavelets, which play a primary role in our theoretical analysis, are calculated for a number of classical wavelet families. Simulation results are finally provided to validate these results.

A Panorama on Multiscale Geometric Representations, Intertwining Spatial, Directional and Frequency Selectivity

The richness of natural images makes the quest for optimal representations in image processing and computer vision challenging. The latter observation has not prevented the design of image representations, which trade off between efficiency and complexity, while achieving accurate rendering of smooth regions as well as reproducing faithful contours and textures. The most recent ones, proposed in the past decade, share an hybrid heritage highlighting the multiscale and oriented nature of edges and patterns in images. This paper presents a panorama of the aforementioned literature on decompositions in multiscale, multi-orientation bases or dictionaries. They typically exhibit redundancy to improve sparsity in the transformed domain and sometimes its invariance with respect to simple geometric deformations (translation, rotation). Oriented multiscale dictionaries extend traditional wavelet processing and may offer rotation invariance. Highly redundant dictionaries require specific algorithms to simplify the search for an efficient (sparse) representation. We also discuss the extension of multiscale geometric decompositions to non-Euclidean domains such as the sphere or arbitrary meshed surfaces. The etymology of panorama suggests an overview, based on a choice of partially overlapping "pictures". We hope that this paper will contribute to the appreciation and apprehension of a stream of current research directions in image understanding.