Annealed Sinkhorn for Optimal Transport: convergence, regularization path and debiasing

Sinkhorn's algorithm is a method of choice to solve large-scale optimal transport (OT) problems. In this context, it involves an inverse temperature parameter $\beta$ that determines the speed-accuracy trade-off. To improve this trade-off, practitioners often use a variant of this algorithm, Annealed Sinkhorn, that uses an nondecreasing sequence $(\beta_t)_{t\in \mathbb{N}}$ where $t$ is the iteration count. However, besides for the schedule $\beta_t=\Theta(\log t)$ which is impractically slow, it is not known whether this variant is guaranteed to actually solve OT. Our first contribution answers this question: we show that a concave annealing schedule asymptotically solves OT if and only if $\beta_t\to+\infty$ and $\beta_t-\beta_{t-1}\to 0$. The proof is based on an equivalence with Online Mirror Descent and further suggests that the iterates of Annealed Sinkhorn follow the solutions of a sequence of relaxed, entropic OT problems, the regularization path. An analysis of this path reveals that, in addition to the well-known "entropic" error in $\Theta(\beta^{-1}_t)$, the annealing procedure induces a "relaxation" error in $\Theta(\beta_{t}-\beta_{t-1})$. The best error trade-off is achieved with the schedule $\beta_t = \Theta(\sqrt{t})$ which, albeit slow, is a universal limitation of this method. Going beyond this limitation, we propose a simple modification of Annealed Sinkhorn that reduces the relaxation error, and therefore enables faster annealing schedules. In toy experiments, we observe the effectiveness of our Debiased Annealed Sinkhorn's algorithm: a single run of this algorithm spans the whole speed-accuracy Pareto front of the standard Sinkhorn's algorithm.

Mean-Field Langevin Dynamics for Signed Measures via a Bilevel Approach

Mean-field Langevin dynamics (MLFD) is a class of interacting particle methods that tackle convex optimization over probability measures on a manifold, which are scalable, versatile, and enjoy computational guarantees. However, some important problems -- such as risk minimization for infinite width two-layer neural networks, or sparse deconvolution -- are originally defined over the set of signed, rather than probability, measures. In this paper, we investigate how to extend the MFLD framework to convex optimization problems over signed measures. Among two known reductions from signed to probability measures -- the lifting and the bilevel approaches -- we show that the bilevel reduction leads to stronger guarantees and faster rates (at the price of a higher per-iteration complexity). In particular, we investigate the convergence rate of MFLD applied to the bilevel reduction in the low-noise regime and obtain two results. First, this dynamics is amenable to an annealing schedule, adapted from Suzuki et al. (2023), that results in improved convergence rates to a fixed multiplicative accuracy. Second, we investigate the problem of learning a single neuron with the bilevel approach and obtain local exponential convergence rates that depend polynomially on the dimension and noise level (to compare with the exponential dependence that would result from prior analyses).

Deep linear networks for regression are implicitly regularized towards flat minima

The largest eigenvalue of the Hessian, or sharpness, of neural networks is a key quantity to understand their optimization dynamics. In this paper, we study the sharpness of deep linear networks for overdetermined univariate regression. Minimizers can have arbitrarily large sharpness, but not an arbitrarily small one. Indeed, we show a lower bound on the sharpness of minimizers, which grows linearly with depth. We then study the properties of the minimizer found by gradient flow, which is the limit of gradient descent with vanishing learning rate. We show an implicit regularization towards flat minima: the sharpness of the minimizer is no more than a constant times the lower bound. The constant depends on the condition number of the data covariance matrix, but not on width or depth. This result is proven both for a small-scale initialization and a residual initialization. Results of independent interest are shown in both cases. For small-scale initialization, we show that the learned weight matrices are approximately rank-one and that their singular vectors align. For residual initialization, convergence of the gradient flow for a Gaussian initialization of the residual network is proven. Numerical experiments illustrate our results and connect them to gradient descent with non-vanishing learning rate.

Steering Deep Feature Learning with Backward Aligned Feature Updates

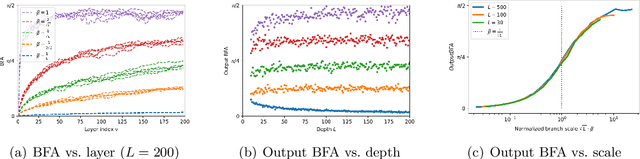
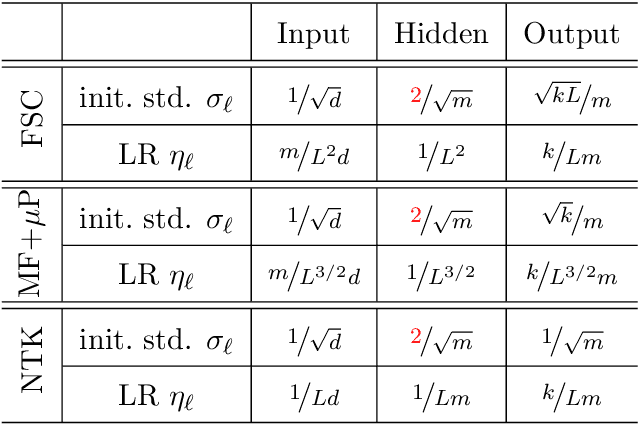
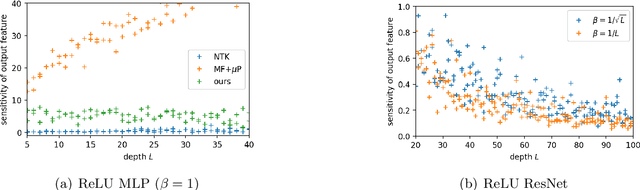
Deep learning succeeds by doing hierarchical feature learning, yet tuning Hyper-Parameters (HP) such as initialization scales, learning rates etc., only give indirect control over this behavior. In this paper, we propose the alignment between the feature updates and the backward pass as a key notion to predict, measure and control feature learning. On the one hand, we show that when alignment holds, the magnitude of feature updates after one SGD step is related to the magnitude of the forward and backward passes by a simple and general formula. This leads to techniques to automatically adjust HPs (initialization scales and learning rates) at initialization and throughout training to attain a desired feature learning behavior. On the other hand, we show that, at random initialization, this alignment is determined by the spectrum of a certain kernel, and that well-conditioned layer-to-layer Jacobians (aka dynamical isometry) implies alignment. Finally, we investigate ReLU MLPs and ResNets in the large width-then-depth limit. Combining hints from random matrix theory and numerical experiments, we show that (i) in MLP with iid initializations, alignment degenerates with depth, making it impossible to start training, and that (ii) in ResNets, the branch scale $1/\sqrt{\text{depth}}$ is the only one maintaining non-trivial alignment at infinite depth.

Computational Guarantees for Doubly Entropic Wasserstein Barycenters via Damped Sinkhorn Iterations

We study the computation of doubly regularized Wasserstein barycenters, a recently introduced family of entropic barycenters governed by inner and outer regularization strengths. Previous research has demonstrated that various regularization parameter choices unify several notions of entropy-penalized barycenters while also revealing new ones, including a special case of debiased barycenters. In this paper, we propose and analyze an algorithm for computing doubly regularized Wasserstein barycenters. Our procedure builds on damped Sinkhorn iterations followed by exact maximization/minimization steps and guarantees convergence for any choice of regularization parameters. An inexact variant of our algorithm, implementable using approximate Monte Carlo sampling, offers the first non-asymptotic convergence guarantees for approximating Wasserstein barycenters between discrete point clouds in the free-support/grid-free setting.

Local Convergence of Gradient Methods for Min-Max Games under Partial Curvature

We study the convergence to local Nash equilibria of gradient methods for two-player zero-sum differentiable games. It is well-known that such dynamics converge locally when $S \succ 0$ and may diverge when $S=0$, where $S\succeq 0$ is the symmetric part of the Jacobian at equilibrium that accounts for the "potential" component of the game. We show that these dynamics also converge as soon as $S$ is nonzero (partial curvature) and the eigenvectors of the antisymmetric part $A$ are in general position with respect to the kernel of $S$. We then study the convergence rates when $S \ll A$ and prove that they typically depend on the average of the eigenvalues of $S$, instead of the minimum as an analogy with minimization problems would suggest. To illustrate our results, we consider the problem of computing mixed Nash equilibria of continuous games. We show that, thanks to partial curvature, conic particle methods -- which optimize over both weights and supports of the mixed strategies -- generically converge faster than fixed-support methods. For min-max games, it is thus beneficial to add degrees of freedom "with curvature": this can be interpreted as yet another benefit of over-parameterization.

On the Effect of Initialization: The Scaling Path of 2-Layer Neural Networks

In supervised learning, the regularization path is sometimes used as a convenient theoretical proxy for the optimization path of gradient descent initialized with zero. In this paper, we study a modification of the regularization path for infinite-width 2-layer ReLU neural networks with non-zero initial distribution of the weights at different scales. By exploiting a link with unbalanced optimal transport theory, we show that, despite the non-convexity of the 2-layer network training, this problem admits an infinite dimensional convex counterpart. We formulate the corresponding functional optimization problem and investigate its main properties. In particular, we show that as the scale of the initialization ranges between $0$ and $+\infty$, the associated path interpolates continuously between the so-called kernel and rich regimes. The numerical experiments confirm that, in our setting, the scaling path and the final states of the optimization path behave similarly even beyond these extreme points.

Doubly Regularized Entropic Wasserstein Barycenters

We study a general formulation of regularized Wasserstein barycenters that enjoys favorable regularity, approximation, stability and (grid-free) optimization properties. This barycenter is defined as the unique probability measure that minimizes the sum of entropic optimal transport (EOT) costs with respect to a family of given probability measures, plus an entropy term. We denote it $(\lambda,\tau)$-barycenter, where $\lambda$ is the inner regularization strength and $\tau$ the outer one. This formulation recovers several previously proposed EOT barycenters for various choices of $\lambda,\tau \geq 0$ and generalizes them. First, in spite of -- and in fact owing to -- being \emph{doubly} regularized, we show that our formulation is debiased for $\tau=\lambda/2$: the suboptimality in the (unregularized) Wasserstein barycenter objective is, for smooth densities, of the order of the strength $\lambda^2$ of entropic regularization, instead of $\max\{\lambda,\tau\}$ in general. We discuss this phenomenon for isotropic Gaussians where all $(\lambda,\tau)$-barycenters have closed form. Second, we show that for $\lambda,\tau>0$, this barycenter has a smooth density and is strongly stable under perturbation of the marginals. In particular, it can be estimated efficiently: given $n$ samples from each of the probability measures, it converges in relative entropy to the population barycenter at a rate $n^{-1/2}$. And finally, this formulation lends itself naturally to a grid-free optimization algorithm: we propose a simple \emph{noisy particle gradient descent} which, in the mean-field limit, converges globally at an exponential rate to the barycenter.

Infinite-width limit of deep linear neural networks

This paper studies the infinite-width limit of deep linear neural networks initialized with random parameters. We obtain that, when the number of neurons diverges, the training dynamics converge (in a precise sense) to the dynamics obtained from a gradient descent on an infinitely wide deterministic linear neural network. Moreover, even if the weights remain random, we get their precise law along the training dynamics, and prove a quantitative convergence result of the linear predictor in terms of the number of neurons. We finally study the continuous-time limit obtained for infinitely wide linear neural networks and show that the linear predictors of the neural network converge at an exponential rate to the minimal $\ell_2$-norm minimizer of the risk.

An Exponentially Converging Particle Method for the Mixed Nash Equilibrium of Continuous Games

We consider the problem of computing mixed Nash equilibria of two-player zero-sum games with continuous sets of pure strategies and with first-order access to the payoff function. This problem arises for example in game-theory-inspired machine learning applications, such as distributionally-robust learning. In those applications, the strategy sets are high-dimensional and thus methods based on discretisation cannot tractably return high-accuracy solutions. In this paper, we introduce and analyze a particle-based method that enjoys guaranteed local convergence for this problem. This method consists in parametrizing the mixed strategies as atomic measures and applying proximal point updates to both the atoms' weights and positions. It can be interpreted as a time-implicit discretization of the "interacting" Wasserstein-Fisher-Rao gradient flow. We prove that, under non-degeneracy assumptions, this method converges at an exponential rate to the exact mixed Nash equilibrium from any initialization satisfying a natural notion of closeness to optimality. We illustrate our results with numerical experiments and discuss applications to max-margin and distributionally-robust classification using two-layer neural networks, where our method has a natural interpretation as a simultaneous training of the network's weights and of the adversarial distribution.