Computational Guarantees for Doubly Entropic Wasserstein Barycenters via Damped Sinkhorn Iterations

We study the computation of doubly regularized Wasserstein barycenters, a recently introduced family of entropic barycenters governed by inner and outer regularization strengths. Previous research has demonstrated that various regularization parameter choices unify several notions of entropy-penalized barycenters while also revealing new ones, including a special case of debiased barycenters. In this paper, we propose and analyze an algorithm for computing doubly regularized Wasserstein barycenters. Our procedure builds on damped Sinkhorn iterations followed by exact maximization/minimization steps and guarantees convergence for any choice of regularization parameters. An inexact variant of our algorithm, implementable using approximate Monte Carlo sampling, offers the first non-asymptotic convergence guarantees for approximating Wasserstein barycenters between discrete point clouds in the free-support/grid-free setting.

Local Risk Bounds for Statistical Aggregation

In the problem of aggregation, the aim is to combine a given class of base predictors to achieve predictions nearly as accurate as the best one. In this flexible framework, no assumption is made on the structure of the class or the nature of the target. Aggregation has been studied in both sequential and statistical contexts. Despite some important differences between the two problems, the classical results in both cases feature the same global complexity measure. In this paper, we revisit and tighten classical results in the theory of aggregation in the statistical setting by replacing the global complexity with a smaller, local one. Some of our proofs build on the PAC-Bayes localization technique introduced by Catoni. Among other results, we prove localized versions of the classical bound for the exponential weights estimator due to Leung and Barron and deviation-optimal bounds for the Q-aggregation estimator. These bounds improve over the results of Dai, Rigollet and Zhang for fixed design regression and the results of Lecu\'e and Rigollet for random design regression.

Distribution-Free Robust Linear Regression

We study random design linear regression with no assumptions on the distribution of the covariates and with a heavy-tailed response variable. When learning without assumptions on the covariates, we establish boundedness of the conditional second moment of the response variable as a necessary and sufficient condition for achieving deviation-optimal excess risk rate of convergence. In particular, combining the ideas of truncated least squares, median-of-means procedures and aggregation theory, we construct a non-linear estimator achieving excess risk of order $d/n$ with the optimal sub-exponential tail. While the existing approaches to learning linear classes under heavy-tailed distributions focus on proper estimators, we highlight that the improperness of our estimator is necessary for attaining non-trivial guarantees in the distribution-free setting considered in this work. Finally, as a byproduct of our analysis, we prove an optimal version of the classical bound for the truncated least squares estimator due to Gy\"{o}rfi, Kohler, Krzyzak, and Walk.

Suboptimality of Constrained Least Squares and Improvements via Non-Linear Predictors

We study the problem of predicting as well as the best linear predictor in a bounded Euclidean ball with respect to the squared loss. When only boundedness of the data generating distribution is assumed, we establish that the least squares estimator constrained to a bounded Euclidean ball does not attain the classical $O(d/n)$ excess risk rate, where $d$ is the dimension of the covariates and $n$ is the number of samples. In particular, we construct a bounded distribution such that the constrained least squares estimator incurs an excess risk of order $\Omega(d^{3/2}/n)$ hence refuting a recent conjecture of Ohad Shamir [JMLR 2015]. In contrast, we observe that non-linear predictors can achieve the optimal rate $O(d/n)$ with no assumptions on the distribution of the covariates. We discuss additional distributional assumptions sufficient to guarantee an $O(d/n)$ excess risk rate for the least squares estimator. Among them are certain moment equivalence assumptions often used in the robust statistics literature. While such assumptions are central in the analysis of unbounded and heavy-tailed settings, our work indicates that in some cases, they also rule out unfavorable bounded distributions.

The Statistical Complexity of Early Stopped Mirror Descent

Recently there has been a surge of interest in understanding implicit regularization properties of iterative gradient-based optimization algorithms. In this paper, we study the statistical guarantees on the excess risk achieved by early stopped unconstrained mirror descent algorithms applied to the unregularized empirical risk with squared loss for linear models and kernel methods. We identify a link between offset Rademacher complexities and potential-based analysis of mirror descent that allows disentangling statistics from optimization in the analysis of such algorithms. Our main result characterizes the statistical performance of the path traced by the iterates of mirror descent in terms of offset complexities of certain function classes depending only on the choice of the mirror map, initialization point, step-size, and number of iterations. We apply our theory to recover, in a rather clean and elegant manner, some of the recent results in the implicit regularization literature, while also showing how to improve upon them in some settings.

Implicit Regularization for Optimal Sparse Recovery

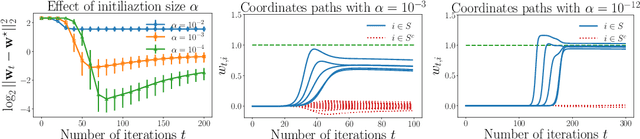
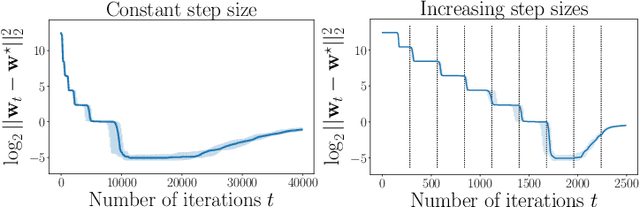
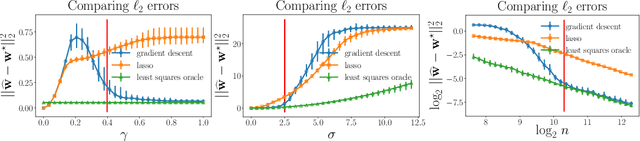
We investigate implicit regularization schemes for gradient descent methods applied to unpenalized least squares regression to solve the problem of reconstructing a sparse signal from an underdetermined system of linear measurements under the restricted isometry assumption. For a given parametrization yielding a non-convex optimization problem, we show that prescribed choices of initialization, step size and stopping time yield a statistically and computationally optimal algorithm that achieves the minimax rate with the same cost required to read the data up to poly-logarithmic factors. Beyond minimax optimality, we show that our algorithm adapts to instance difficulty and yields a dimension-independent rate when the signal-to-noise ratio is high enough. Key to the computational efficiency of our method is an increasing step size scheme that adapts to refined estimates of the true solution. We validate our findings with numerical experiments and compare our algorithm against explicit $\ell_{1}$ penalization. Going from hard instances to easy ones, our algorithm is seen to undergo a phase transition, eventually matching least squares with an oracle knowledge of the true support.