Varun Kanade
Provably Learning Attention with Queries
Jan 23, 2026Abstract:We study the problem of learning Transformer-based sequence models with black-box access to their outputs. In this setting, a learner may adaptively query the oracle with any sequence of vectors and observe the corresponding real-valued output. We begin with the simplest case, a single-head softmax-attention regressor. We show that for a model with width $d$, there is an elementary algorithm to learn the parameters of single-head attention exactly with $O(d^2)$ queries. Further, we show that if there exists an algorithm to learn ReLU feedforward networks (FFNs), then the single-head algorithm can be easily adapted to learn one-layer Transformers with single-head attention. Next, motivated by the regime where the head dimension $r \ll d$, we provide a randomised algorithm that learns single-head attention-based models with $O(rd)$ queries via compressed sensing arguments. We also study robustness to noisy oracle access, proving that under mild norm and margin conditions, the parameters can be estimated to $\varepsilon$ accuracy with a polynomial number of queries even when outputs are only provided up to additive tolerance. Finally, we show that multi-head attention parameters are not identifiable from value queries in general -- distinct parameterisations can induce the same input-output map. Hence, guarantees analogous to the single-head setting are impossible without additional structural assumptions.
DEEDEE: Fast and Scalable Out-of-Distribution Dynamics Detection
Oct 24, 2025Abstract:Deploying reinforcement learning (RL) in safety-critical settings is constrained by brittleness under distribution shift. We study out-of-distribution (OOD) detection for RL time series and introduce DEEDEE, a two-statistic detector that revisits representation-heavy pipelines with a minimal alternative. DEEDEE uses only an episodewise mean and an RBF kernel similarity to a training summary, capturing complementary global and local deviations. Despite its simplicity, DEEDEE matches or surpasses contemporary detectors across standard RL OOD suites, delivering a 600-fold reduction in compute (FLOPs / wall-time) and an average 5% absolute accuracy gain over strong baselines. Conceptually, our results indicate that diverse anomaly types often imprint on RL trajectories through a small set of low-order statistics, suggesting a compact foundation for OOD detection in complex environments.
Pause Tokens Strictly Increase the Expressivity of Constant-Depth Transformers
May 27, 2025Abstract:Pause tokens, simple filler symbols such as "...", consistently improve Transformer performance on both language and mathematical tasks, yet their theoretical effect remains unexplained. We provide the first formal separation result, proving that adding pause tokens to constant-depth, logarithmic-width Transformers strictly increases their computational expressivity. With bounded-precision activations, Transformers without pause tokens compute only a strict subset of $\mathsf{AC}^0$ functions, while adding a polynomial number of pause tokens allows them to express the entire class. For logarithmic-precision Transformers, we show that adding pause tokens achieves expressivity equivalent to $\mathsf{TC}^0$, matching known upper bounds. Empirically, we demonstrate that two-layer causally masked Transformers can learn parity when supplied with pause tokens, a function that they appear unable to learn without them. Our results provide a rigorous theoretical explanation for prior empirical findings, clarify how pause tokens interact with width, depth, and numeric precision, and position them as a distinct mechanism, complementary to chain-of-thought prompting, for enhancing Transformer reasoning.
How Global Calibration Strengthens Multiaccuracy
Apr 21, 2025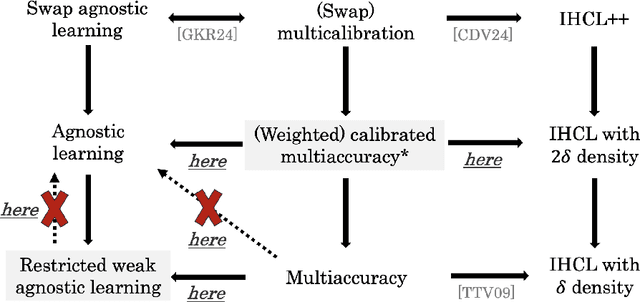
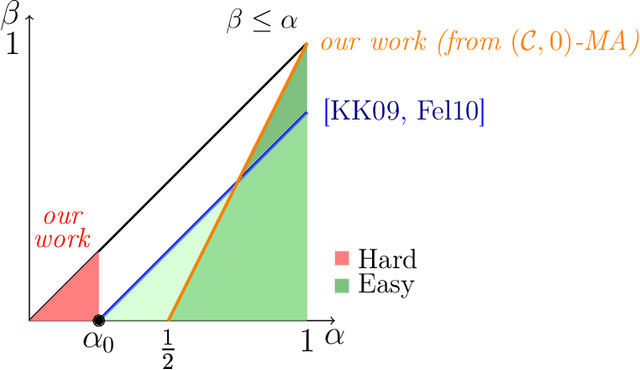

Abstract:Multiaccuracy and multicalibration are multigroup fairness notions for prediction that have found numerous applications in learning and computational complexity. They can be achieved from a single learning primitive: weak agnostic learning. Here we investigate the power of multiaccuracy as a learning primitive, both with and without the additional assumption of calibration. We find that multiaccuracy in itself is rather weak, but that the addition of global calibration (this notion is called calibrated multiaccuracy) boosts its power substantially, enough to recover implications that were previously known only assuming the stronger notion of multicalibration. We give evidence that multiaccuracy might not be as powerful as standard weak agnostic learning, by showing that there is no way to post-process a multiaccurate predictor to get a weak learner, even assuming the best hypothesis has correlation $1/2$. Rather, we show that it yields a restricted form of weak agnostic learning, which requires some concept in the class to have correlation greater than $1/2$ with the labels. However, by also requiring the predictor to be calibrated, we recover not just weak, but strong agnostic learning. A similar picture emerges when we consider the derivation of hardcore measures from predictors satisfying multigroup fairness notions. On the one hand, while multiaccuracy only yields hardcore measures of density half the optimal, we show that (a weighted version of) calibrated multiaccuracy achieves optimal density. Our results yield new insights into the complementary roles played by multiaccuracy and calibration in each setting. They shed light on why multiaccuracy and global calibration, although not particularly powerful by themselves, together yield considerably stronger notions.
Separations in the Representational Capabilities of Transformers and Recurrent Architectures
Jun 13, 2024Abstract:Transformer architectures have been widely adopted in foundation models. Due to their high inference costs, there is renewed interest in exploring the potential of efficient recurrent architectures (RNNs). In this paper, we analyze the differences in the representational capabilities of Transformers and RNNs across several tasks of practical relevance, including index lookup, nearest neighbor, recognizing bounded Dyck languages, and string equality. For the tasks considered, our results show separations based on the size of the model required for different architectures. For example, we show that a one-layer Transformer of logarithmic width can perform index lookup, whereas an RNN requires a hidden state of linear size. Conversely, while constant-size RNNs can recognize bounded Dyck languages, we show that one-layer Transformers require a linear size for this task. Furthermore, we show that two-layer Transformers of logarithmic size can perform decision tasks such as string equality or disjointness, whereas both one-layer Transformers and recurrent models require linear size for these tasks. We also show that a log-size two-layer Transformer can implement the nearest neighbor algorithm in its forward pass; on the other hand recurrent models require linear size. Our constructions are based on the existence of $N$ nearly orthogonal vectors in $O(\log N)$ dimensional space and our lower bounds are based on reductions from communication complexity problems. We supplement our theoretical results with experiments that highlight the differences in the performance of these architectures on practical-size sequences.
Understanding In-Context Learning in Transformers and LLMs by Learning to Learn Discrete Functions
Oct 04, 2023



Abstract:In order to understand the in-context learning phenomenon, recent works have adopted a stylized experimental framework and demonstrated that Transformers can learn gradient-based learning algorithms for various classes of real-valued functions. However, the limitations of Transformers in implementing learning algorithms, and their ability to learn other forms of algorithms are not well understood. Additionally, the degree to which these capabilities are confined to attention-based models is unclear. Furthermore, it remains to be seen whether the insights derived from these stylized settings can be extrapolated to pretrained Large Language Models (LLMs). In this work, we take a step towards answering these questions by demonstrating the following: (a) On a test-bed with a variety of Boolean function classes, we find that Transformers can nearly match the optimal learning algorithm for 'simpler' tasks, while their performance deteriorates on more 'complex' tasks. Additionally, we find that certain attention-free models perform (almost) identically to Transformers on a range of tasks. (b) When provided a teaching sequence, i.e. a set of examples that uniquely identifies a function in a class, we show that Transformers learn more sample-efficiently. Interestingly, our results show that Transformers can learn to implement two distinct algorithms to solve a single task, and can adaptively select the more sample-efficient algorithm depending on the sequence of in-context examples. (c) Lastly, we show that extant LLMs, e.g. LLaMA-2, GPT-4, can compete with nearest-neighbor baselines on prediction tasks that are guaranteed to not be in their training set.
Simplicity Bias in Transformers and their Ability to Learn Sparse Boolean Functions
Nov 22, 2022



Abstract:Despite the widespread success of Transformers on NLP tasks, recent works have found that they struggle to model several formal languages when compared to recurrent models. This raises the question of why Transformers perform well in practice and whether they have any properties that enable them to generalize better than recurrent models. In this work, we conduct an extensive empirical study on Boolean functions to demonstrate the following: (i) Random Transformers are relatively more biased towards functions of low sensitivity. (ii) When trained on Boolean functions, both Transformers and LSTMs prioritize learning functions of low sensitivity, with Transformers ultimately converging to functions of lower sensitivity. (iii) On sparse Boolean functions which have low sensitivity, we find that Transformers generalize near perfectly even in the presence of noisy labels whereas LSTMs overfit and achieve poor generalization accuracy. Overall, our results provide strong quantifiable evidence that suggests differences in the inductive biases of Transformers and recurrent models which may help explain Transformer's effective generalization performance despite relatively limited expressiveness.
When are Local Queries Useful for Robust Learning?
Oct 12, 2022

Abstract:Distributional assumptions have been shown to be necessary for the robust learnability of concept classes when considering the exact-in-the-ball robust risk and access to random examples by Gourdeau et al. (2019). In this paper, we study learning models where the learner is given more power through the use of local queries, and give the first distribution-free algorithms that perform robust empirical risk minimization (ERM) for this notion of robustness. The first learning model we consider uses local membership queries (LMQ), where the learner can query the label of points near the training sample. We show that, under the uniform distribution, LMQs do not increase the robustness threshold of conjunctions and any superclass, e.g., decision lists and halfspaces. Faced with this negative result, we introduce the local equivalence query (LEQ) oracle, which returns whether the hypothesis and target concept agree in the perturbation region around a point in the training sample, as well as a counterexample if it exists. We show a separation result: on one hand, if the query radius $\lambda$ is strictly smaller than the adversary's perturbation budget $\rho$, then distribution-free robust learning is impossible for a wide variety of concept classes; on the other hand, the setting $\lambda=\rho$ allows us to develop robust ERM algorithms. We then bound the query complexity of these algorithms based on online learning guarantees and further improve these bounds for the special case of conjunctions. We finish by giving robust learning algorithms for halfspaces with margins on both $\{0,1\}^n$ and $\mathbb{R}^n$.
Partial Matrix Completion
Aug 25, 2022
Abstract:In the matrix completion problem, one wishes to reconstruct a low-rank matrix based on a revealed set of (possibly noisy) entries. Prior work considers completing the entire matrix, which may be highly inaccurate in the common case where the distribution over entries is non-uniform. We formalize the problem of Partial Matrix Completion where the goal is to complete a large subset of the entries, or equivalently to complete the entire matrix and specify an accurate subset of the entries. Interestingly, even though the distribution is unknown and arbitrarily complex, our efficient algorithm is able to guarantee: (a) high accuracy over all completed entries, and (b) high coverage, meaning that it covers at least as much of the matrix as the distribution of observations.
Beyond Impossibility: Balancing Sufficiency, Separation and Accuracy
May 24, 2022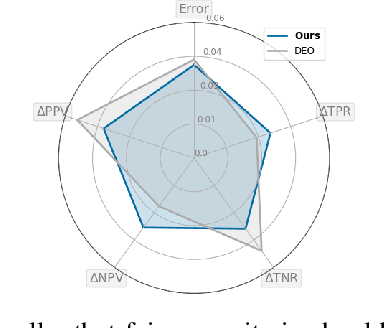

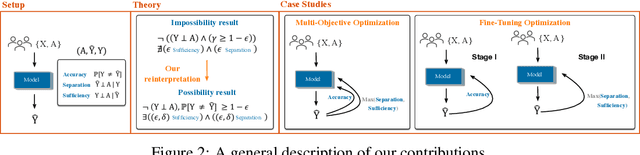
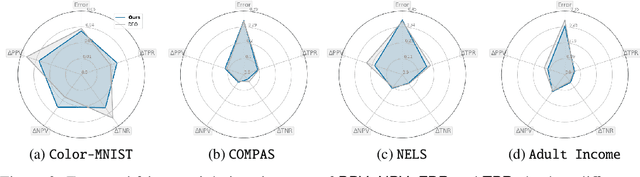
Abstract:Among the various aspects of algorithmic fairness studied in recent years, the tension between satisfying both \textit{sufficiency} and \textit{separation} -- e.g. the ratios of positive or negative predictive values, and false positive or false negative rates across groups -- has received much attention. Following a debate sparked by COMPAS, a criminal justice predictive system, the academic community has responded by laying out important theoretical understanding, showing that one cannot achieve both with an imperfect predictor when there is no equal distribution of labels across the groups. In this paper, we shed more light on what might be still possible beyond the impossibility -- the existence of a trade-off means we should aim to find a good balance within it. After refining the existing theoretical result, we propose an objective that aims to balance \textit{sufficiency} and \textit{separation} measures, while maintaining similar accuracy levels. We show the use of such an objective in two empirical case studies, one involving a multi-objective framework, and the other fine-tuning of a model pre-trained for accuracy. We show promising results, where better trade-offs are achieved compared to existing alternatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge