Functional Causal Bayesian Optimization

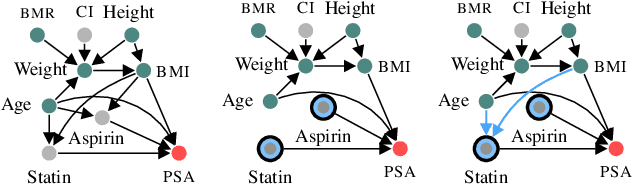
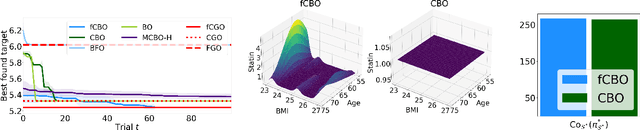
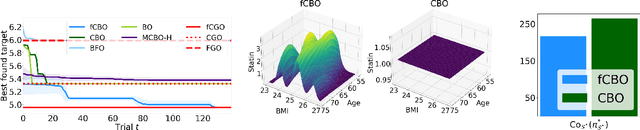
We propose functional causal Bayesian optimization (fCBO), a method for finding interventions that optimize a target variable in a known causal graph. fCBO extends the CBO family of methods to enable functional interventions, which set a variable to be a deterministic function of other variables in the graph. fCBO models the unknown objectives with Gaussian processes whose inputs are defined in a reproducing kernel Hilbert space, thus allowing to compute distances among vector-valued functions. In turn, this enables to sequentially select functions to explore by maximizing an expected improvement acquisition functional while keeping the typical computational tractability of standard BO settings. We introduce graphical criteria that establish when considering functional interventions allows attaining better target effects, and conditions under which selected interventions are also optimal for conditional target effects. We demonstrate the benefits of the method in a synthetic and in a real-world causal graph.

Pragmatic Fairness: Developing Policies with Outcome Disparity Control

We introduce a causal framework for designing optimal policies that satisfy fairness constraints. We take a pragmatic approach asking what we can do with an action space available to us and only with access to historical data. We propose two different fairness constraints: a moderation breaking constraint which aims at blocking moderation paths from the action and sensitive attribute to the outcome, and by that at reducing disparity in outcome levels as much as the provided action space permits; and an equal benefit constraint which aims at distributing gain from the new and maximized policy equally across sensitive attribute levels, and thus at keeping pre-existing preferential treatment in place or avoiding the introduction of new disparity. We introduce practical methods for implementing the constraints and illustrate their uses on experiments with semi-synthetic models.

Causal Inference with Treatment Measurement Error: A Nonparametric Instrumental Variable Approach

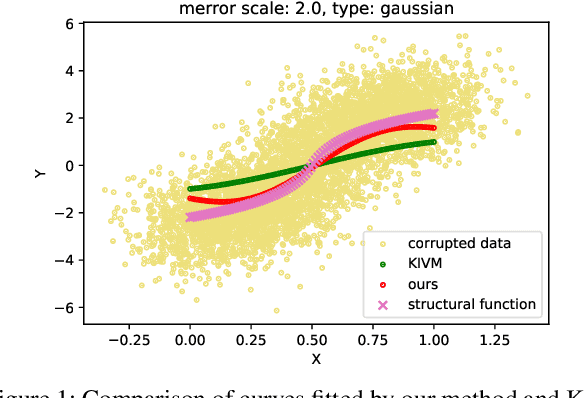
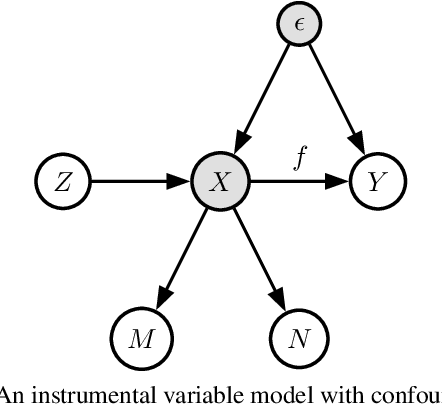
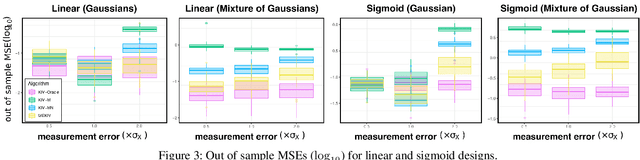
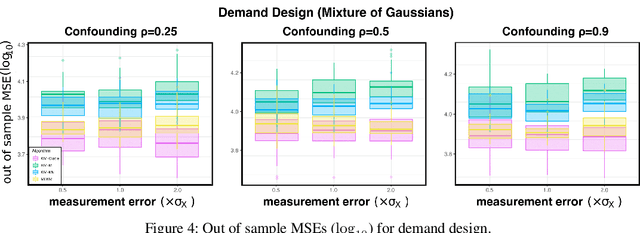
We propose a kernel-based nonparametric estimator for the causal effect when the cause is corrupted by error. We do so by generalizing estimation in the instrumental variable setting. Despite significant work on regression with measurement error, additionally handling unobserved confounding in the continuous setting is non-trivial: we have seen little prior work. As a by-product of our investigation, we clarify a connection between mean embeddings and characteristic functions, and how learning one simultaneously allows one to learn the other. This opens the way for kernel method research to leverage existing results in characteristic function estimation. Finally, we empirically show that our proposed method, MEKIV, improves over baselines and is robust under changes in the strength of measurement error and to the type of error distributions.

Beyond Impossibility: Balancing Sufficiency, Separation and Accuracy

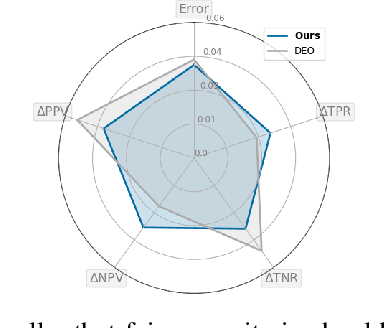
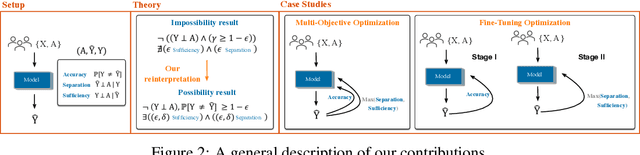
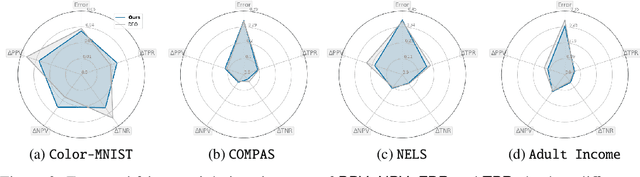
Among the various aspects of algorithmic fairness studied in recent years, the tension between satisfying both \textit{sufficiency} and \textit{separation} -- e.g. the ratios of positive or negative predictive values, and false positive or false negative rates across groups -- has received much attention. Following a debate sparked by COMPAS, a criminal justice predictive system, the academic community has responded by laying out important theoretical understanding, showing that one cannot achieve both with an imperfect predictor when there is no equal distribution of labels across the groups. In this paper, we shed more light on what might be still possible beyond the impossibility -- the existence of a trade-off means we should aim to find a good balance within it. After refining the existing theoretical result, we propose an objective that aims to balance \textit{sufficiency} and \textit{separation} measures, while maintaining similar accuracy levels. We show the use of such an objective in two empirical case studies, one involving a multi-objective framework, and the other fine-tuning of a model pre-trained for accuracy. We show promising results, where better trade-offs are achieved compared to existing alternatives.

Operationalizing Complex Causes: A Pragmatic View of Mediation

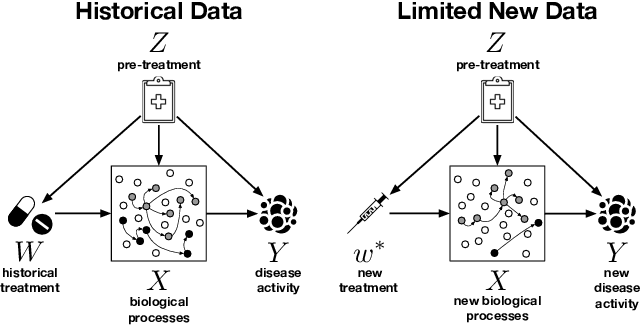
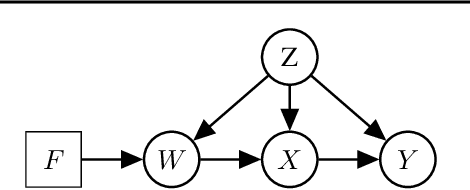
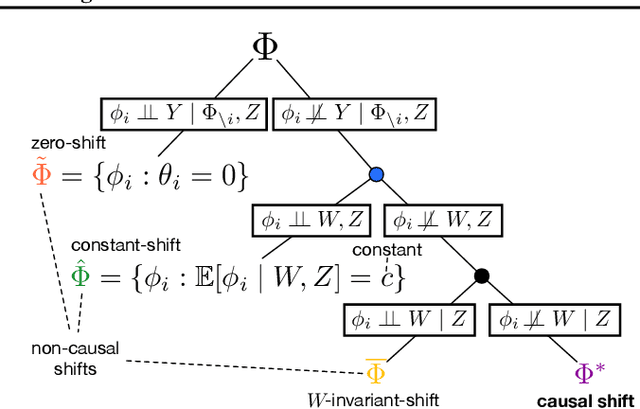
We examine the problem of causal response estimation for complex objects (e.g., text, images, genomics). In this setting, classical \emph{atomic} interventions are often not available (e.g., changes to characters, pixels, DNA base-pairs). Instead, we only have access to indirect or \emph{crude} interventions (e.g., enrolling in a writing program, modifying a scene, applying a gene therapy). In this work, we formalize this problem and provide an initial solution. Given a collection of candidate mediators, we propose (a) a two-step method for predicting the causal responses of crude interventions; and (b) a testing procedure to identify mediators of crude interventions. We demonstrate, on a range of simulated and real-world-inspired examples, that our approach allows us to efficiently estimate the effect of crude interventions with limited data from new treatment regimes.

Proximal Causal Learning with Kernels: Two-Stage Estimation and Moment Restriction

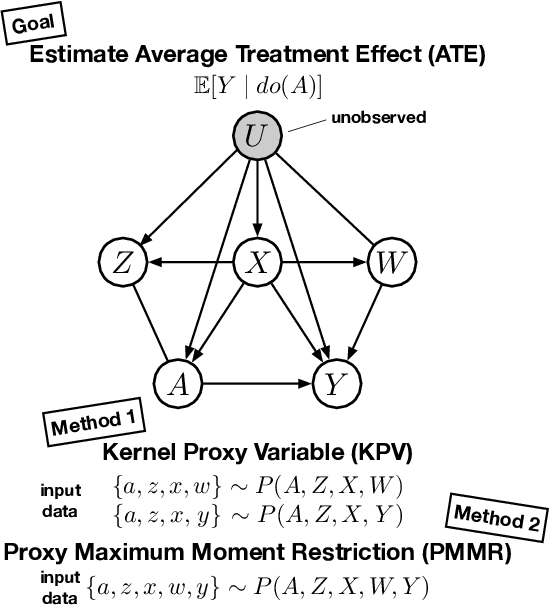
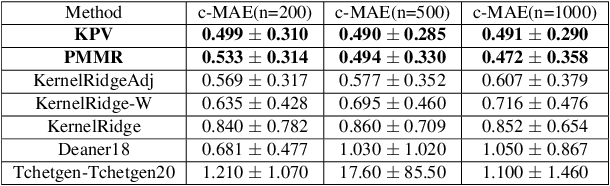
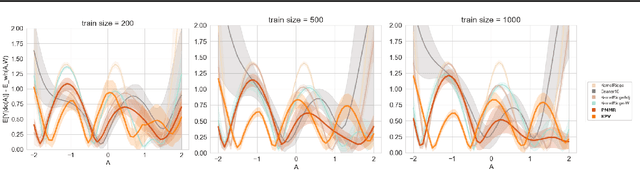
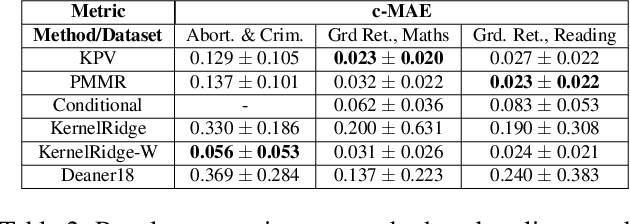
We address the problem of causal effect estimation in the presence of unobserved confounding, but where proxies for the latent confounder(s) are observed. We propose two kernel-based methods for nonlinear causal effect estimation in this setting: (a) a two-stage regression approach, and (b) a maximum moment restriction approach. We focus on the proximal causal learning setting, but our methods can be used to solve a wider class of inverse problems characterised by a Fredholm integral equation. In particular, we provide a unifying view of two-stage and moment restriction approaches for solving this problem in a nonlinear setting. We provide consistency guarantees for each algorithm, and we demonstrate these approaches achieve competitive results on synthetic data and data simulating a real-world task. In particular, our approach outperforms earlier methods that are not suited to leveraging proxy variables.

Local Explanations via Necessity and Sufficiency: Unifying Theory and Practice

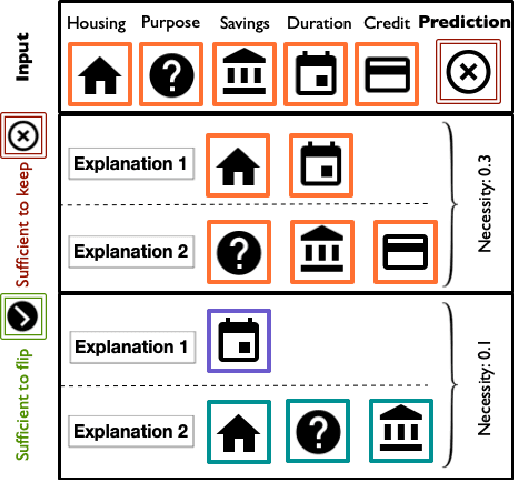
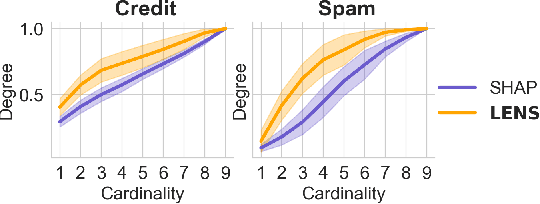
Necessity and sufficiency are the building blocks of all successful explanations. Yet despite their importance, these notions have been conceptually underdeveloped and inconsistently applied in explainable artificial intelligence (XAI), a fast-growing research area that is so far lacking in firm theoretical foundations. Building on work in logic, probability, and causality, we establish the central role of necessity and sufficiency in XAI, unifying seemingly disparate methods in a single formal framework. We provide a sound and complete algorithm for computing explanatory factors with respect to a given context, and demonstrate its flexibility and competitive performance against state of the art alternatives on various tasks.

Differentiable Causal Backdoor Discovery

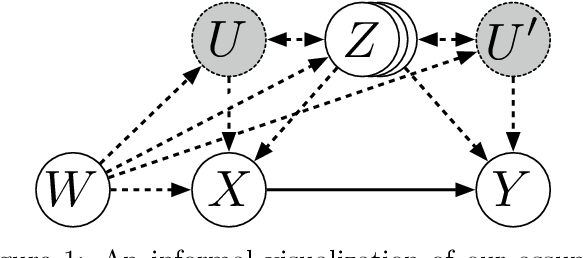
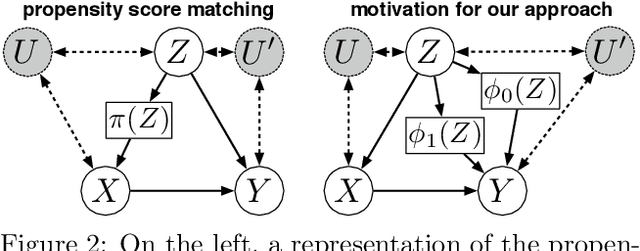
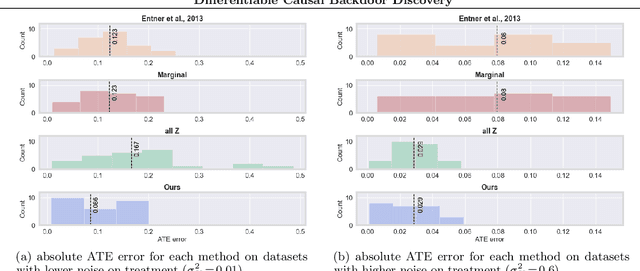
Discovering the causal effect of a decision is critical to nearly all forms of decision-making. In particular, it is a key quantity in drug development, in crafting government policy, and when implementing a real-world machine learning system. Given only observational data, confounders often obscure the true causal effect. Luckily, in some cases, it is possible to recover the causal effect by using certain observed variables to adjust for the effects of confounders. However, without access to the true causal model, finding this adjustment requires brute-force search. In this work, we present an algorithm that exploits auxiliary variables, similar to instruments, in order to find an appropriate adjustment by a gradient-based optimization method. We demonstrate that it outperforms practical alternatives in estimating the true causal effect, without knowledge of the full causal graph.

Humor in Word Embeddings: Cockamamie Gobbledegook for Nincompoops

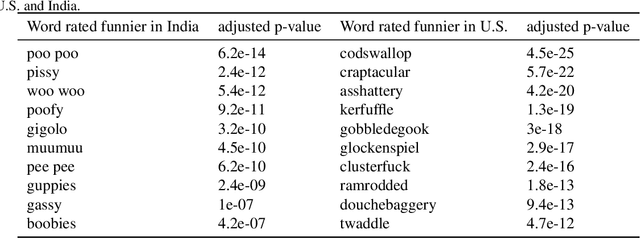
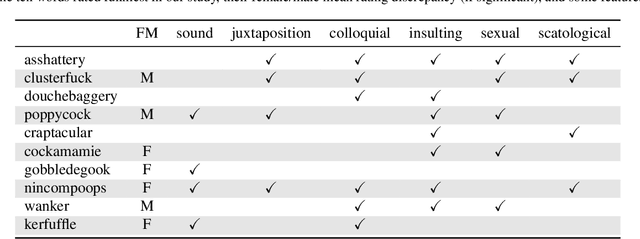
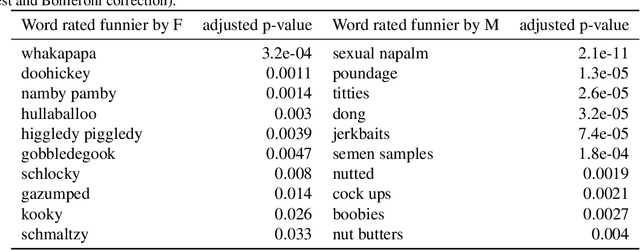
We study humor in Word Embeddings, a popular AI tool that associates each word with a Euclidean vector. We find that: (a) the word vectors capture multiple aspects of humor discussed in theories of humor; and (b) each individual's sense of humor can be represented by a vector, and that these sense-of-humor vectors accurately predict differences in people's sense of humor on new, unrated, words. The fact that single-word humor seems to be relatively easy for AI has implications for the study of humor in language. Humor ratings are taken from the work of Englethaler and Hills (2017) as well as our own crowdsourcing study of 120,000 words.