Proximal Causal Learning with Kernels: Two-Stage Estimation and Moment Restriction
Paper and Code
Jun 06, 2021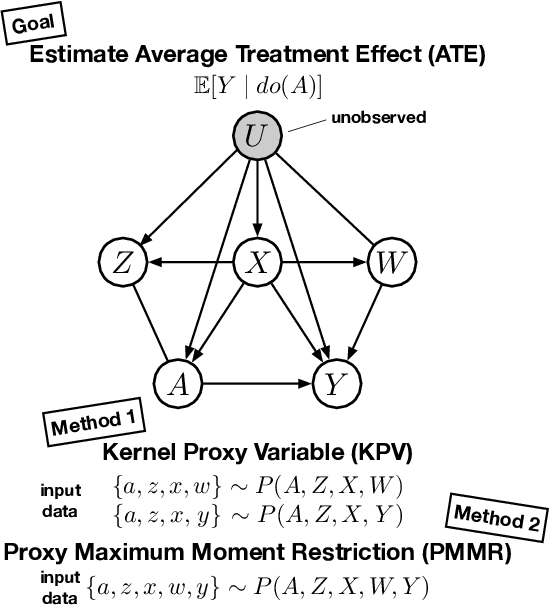
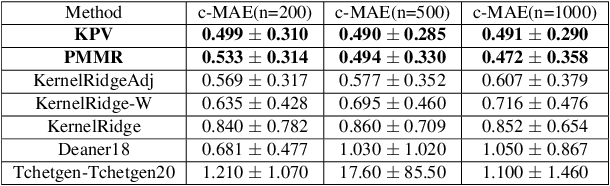
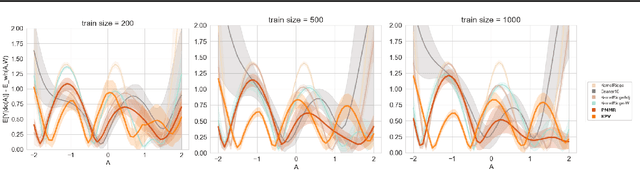
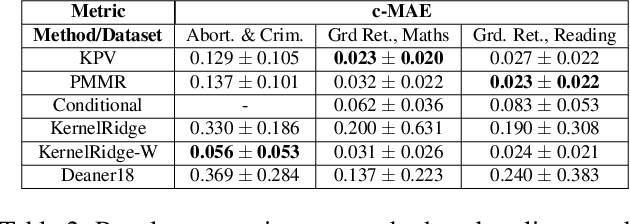
We address the problem of causal effect estimation in the presence of unobserved confounding, but where proxies for the latent confounder(s) are observed. We propose two kernel-based methods for nonlinear causal effect estimation in this setting: (a) a two-stage regression approach, and (b) a maximum moment restriction approach. We focus on the proximal causal learning setting, but our methods can be used to solve a wider class of inverse problems characterised by a Fredholm integral equation. In particular, we provide a unifying view of two-stage and moment restriction approaches for solving this problem in a nonlinear setting. We provide consistency guarantees for each algorithm, and we demonstrate these approaches achieve competitive results on synthetic data and data simulating a real-world task. In particular, our approach outperforms earlier methods that are not suited to leveraging proxy variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge