Arthur Gretton
E3S
Closed-Form Last Layer Optimization
Oct 06, 2025Abstract:Neural networks are typically optimized with variants of stochastic gradient descent. Under a squared loss, however, the optimal solution to the linear last layer weights is known in closed-form. We propose to leverage this during optimization, treating the last layer as a function of the backbone parameters, and optimizing solely for these parameters. We show this is equivalent to alternating between gradient descent steps on the backbone and closed-form updates on the last layer. We adapt the method for the setting of stochastic gradient descent, by trading off the loss on the current batch against the accumulated information from previous batches. Further, we prove that, in the Neural Tangent Kernel regime, convergence of this method to an optimal solution is guaranteed. Finally, we demonstrate the effectiveness of our approach compared with standard SGD on a squared loss in several supervised tasks -- both regression and classification -- including Fourier Neural Operators and Instrumental Variable Regression.
Learn to Guide Your Diffusion Model
Oct 01, 2025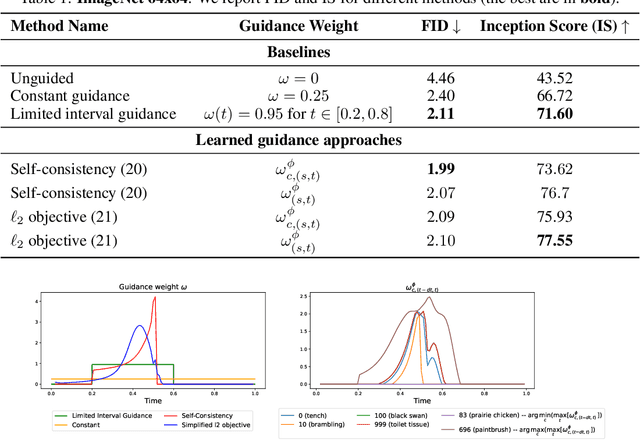
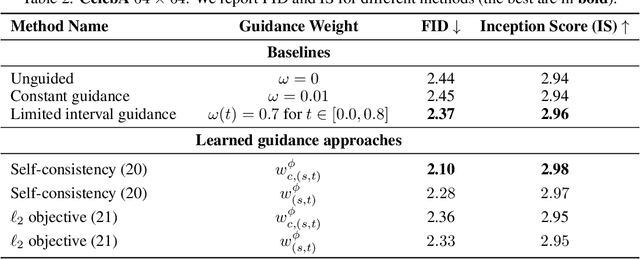
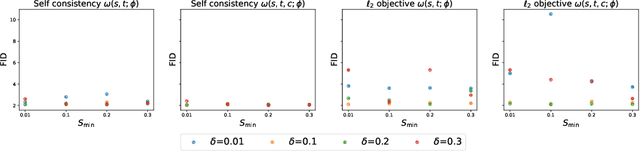

Abstract:Classifier-free guidance (CFG) is a widely used technique for improving the perceptual quality of samples from conditional diffusion models. It operates by linearly combining conditional and unconditional score estimates using a guidance weight $\omega$. While a large, static weight can markedly improve visual results, this often comes at the cost of poorer distributional alignment. In order to better approximate the target conditional distribution, we instead learn guidance weights $\omega_{c,(s,t)}$, which are continuous functions of the conditioning $c$, the time $t$ from which we denoise, and the time $s$ towards which we denoise. We achieve this by minimizing the distributional mismatch between noised samples from the true conditional distribution and samples from the guided diffusion process. We extend our framework to reward guided sampling, enabling the model to target distributions tilted by a reward function $R(x_0,c)$, defined on clean data and a conditioning $c$. We demonstrate the effectiveness of our methodology on low-dimensional toy examples and high-dimensional image settings, where we observe improvements in Fr\'echet inception distance (FID) for image generation. In text-to-image applications, we observe that employing a reward function given by the CLIP score leads to guidance weights that improve image-prompt alignment.
Demystifying Spectral Feature Learning for Instrumental Variable Regression
Jun 12, 2025Abstract:We address the problem of causal effect estimation in the presence of hidden confounders, using nonparametric instrumental variable (IV) regression. A leading strategy employs spectral features - that is, learned features spanning the top eigensubspaces of the operator linking treatments to instruments. We derive a generalization error bound for a two-stage least squares estimator based on spectral features, and gain insights into the method's performance and failure modes. We show that performance depends on two key factors, leading to a clear taxonomy of outcomes. In a good scenario, the approach is optimal. This occurs with strong spectral alignment, meaning the structural function is well-represented by the top eigenfunctions of the conditional operator, coupled with this operator's slow eigenvalue decay, indicating a strong instrument. Performance degrades in a bad scenario: spectral alignment remains strong, but rapid eigenvalue decay (indicating a weaker instrument) demands significantly more samples for effective feature learning. Finally, in the ugly scenario, weak spectral alignment causes the method to fail, regardless of the eigenvalues' characteristics. Our synthetic experiments empirically validate this taxonomy.
Density Ratio-Free Doubly Robust Proxy Causal Learning
May 26, 2025Abstract:We study the problem of causal function estimation in the Proxy Causal Learning (PCL) framework, where confounders are not observed but proxies for the confounders are available. Two main approaches have been proposed: outcome bridge-based and treatment bridge-based methods. In this work, we propose two kernel-based doubly robust estimators that combine the strengths of both approaches, and naturally handle continuous and high-dimensional variables. Our identification strategy builds on a recent density ratio-free method for treatment bridge-based PCL; furthermore, in contrast to previous approaches, it does not require indicator functions or kernel smoothing over the treatment variable. These properties make it especially well-suited for continuous or high-dimensional treatments. By using kernel mean embeddings, we have closed-form solutions and strong consistency guarantees. Our estimators outperform existing methods on PCL benchmarks, including a prior doubly robust method that requires both kernel smoothing and density ratio estimation.
Regularized least squares learning with heavy-tailed noise is minimax optimal
May 20, 2025Abstract:This paper examines the performance of ridge regression in reproducing kernel Hilbert spaces in the presence of noise that exhibits a finite number of higher moments. We establish excess risk bounds consisting of subgaussian and polynomial terms based on the well known integral operator framework. The dominant subgaussian component allows to achieve convergence rates that have previously only been derived under subexponential noise - a prevalent assumption in related work from the last two decades. These rates are optimal under standard eigenvalue decay conditions, demonstrating the asymptotic robustness of regularized least squares against heavy-tailed noise. Our derivations are based on a Fuk-Nagaev inequality for Hilbert-space valued random variables.
Density Ratio-based Proxy Causal Learning Without Density Ratios
Mar 11, 2025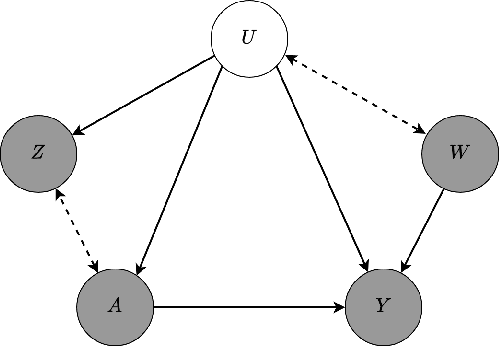
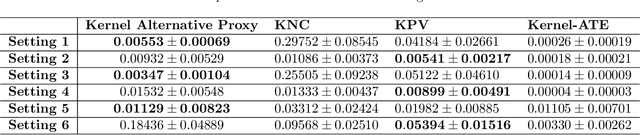
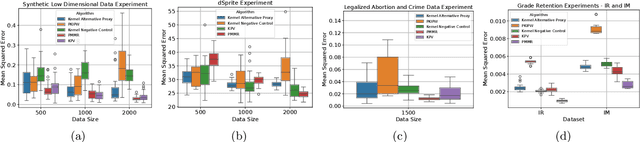
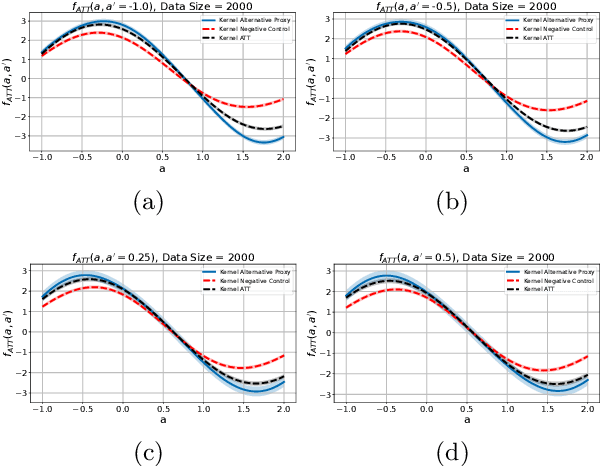
Abstract:We address the setting of Proxy Causal Learning (PCL), which has the goal of estimating causal effects from observed data in the presence of hidden confounding. Proxy methods accomplish this task using two proxy variables related to the latent confounder: a treatment proxy (related to the treatment) and an outcome proxy (related to the outcome). Two approaches have been proposed to perform causal effect estimation given proxy variables; however only one of these has found mainstream acceptance, since the other was understood to require density ratio estimation - a challenging task in high dimensions. In the present work, we propose a practical and effective implementation of the second approach, which bypasses explicit density ratio estimation and is suitable for continuous and high-dimensional treatments. We employ kernel ridge regression to derive estimators, resulting in simple closed-form solutions for dose-response and conditional dose-response curves, along with consistency guarantees. Our methods empirically demonstrate superior or comparable performance to existing frameworks on synthetic and real-world datasets.
Learning-Order Autoregressive Models with Application to Molecular Graph Generation
Mar 07, 2025Abstract:Autoregressive models (ARMs) have become the workhorse for sequence generation tasks, since many problems can be modeled as next-token prediction. While there appears to be a natural ordering for text (i.e., left-to-right), for many data types, such as graphs, the canonical ordering is less obvious. To address this problem, we introduce a variant of ARM that generates high-dimensional data using a probabilistic ordering that is sequentially inferred from data. This model incorporates a trainable probability distribution, referred to as an \emph{order-policy}, that dynamically decides the autoregressive order in a state-dependent manner. To train the model, we introduce a variational lower bound on the exact log-likelihood, which we optimize with stochastic gradient estimation. We demonstrate experimentally that our method can learn meaningful autoregressive orderings in image and graph generation. On the challenging domain of molecular graph generation, we achieve state-of-the-art results on the QM9 and ZINC250k benchmarks, evaluated using the Fr\'{e}chet ChemNet Distance (FCD).
Sleepless Nights, Sugary Days: Creating Synthetic Users with Health Conditions for Realistic Coaching Agent Interactions
Feb 18, 2025Abstract:We present an end-to-end framework for generating synthetic users for evaluating interactive agents designed to encourage positive behavior changes, such as in health and lifestyle coaching. The synthetic users are grounded in health and lifestyle conditions, specifically sleep and diabetes management in this study, to ensure realistic interactions with the health coaching agent. Synthetic users are created in two stages: first, structured data are generated grounded in real-world health and lifestyle factors in addition to basic demographics and behavioral attributes; second, full profiles of the synthetic users are developed conditioned on the structured data. Interactions between synthetic users and the coaching agent are simulated using generative agent-based models such as Concordia, or directly by prompting a language model. Using two independently-developed agents for sleep and diabetes coaching as case studies, the validity of this framework is demonstrated by analyzing the coaching agent's understanding of the synthetic users' needs and challenges. Finally, through multiple blinded evaluations of user-coach interactions by human experts, we demonstrate that our synthetic users with health and behavioral attributes more accurately portray real human users with the same attributes, compared to generic synthetic users not grounded in such attributes. The proposed framework lays the foundation for efficient development of conversational agents through extensive, realistic, and grounded simulated interactions.
Distributional Diffusion Models with Scoring Rules
Feb 04, 2025Abstract:Diffusion models generate high-quality synthetic data. They operate by defining a continuous-time forward process which gradually adds Gaussian noise to data until fully corrupted. The corresponding reverse process progressively "denoises" a Gaussian sample into a sample from the data distribution. However, generating high-quality outputs requires many discretization steps to obtain a faithful approximation of the reverse process. This is expensive and has motivated the development of many acceleration methods. We propose to accomplish sample generation by learning the posterior {\em distribution} of clean data samples given their noisy versions, instead of only the mean of this distribution. This allows us to sample from the probability transitions of the reverse process on a coarse time scale, significantly accelerating inference with minimal degradation of the quality of the output. This is accomplished by replacing the standard regression loss used to estimate conditional means with a scoring rule. We validate our method on image and robot trajectory generation, where we consistently outperform standard diffusion models at few discretization steps.
Accelerated Diffusion Models via Speculative Sampling
Jan 09, 2025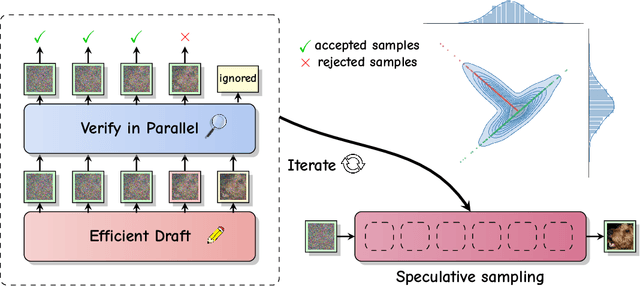
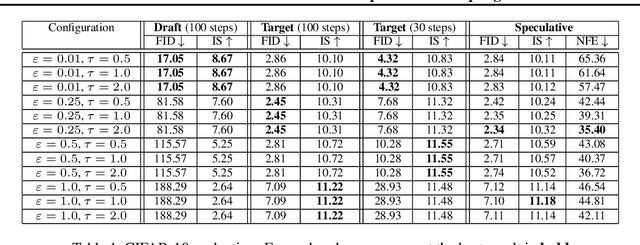
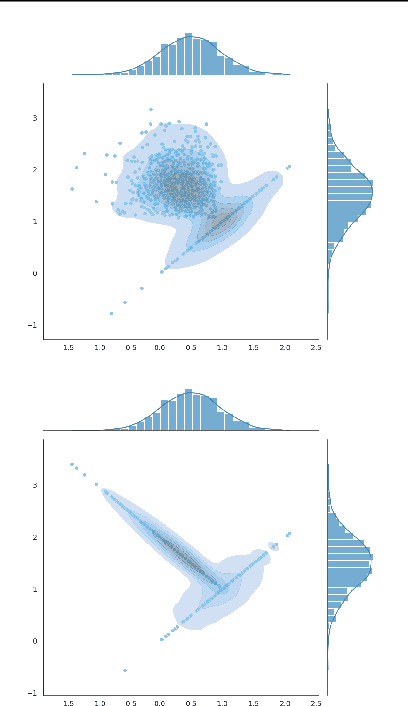
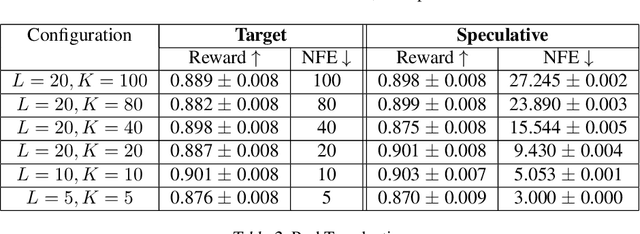
Abstract:Speculative sampling is a popular technique for accelerating inference in Large Language Models by generating candidate tokens using a fast draft model and accepting or rejecting them based on the target model's distribution. While speculative sampling was previously limited to discrete sequences, we extend it to diffusion models, which generate samples via continuous, vector-valued Markov chains. In this context, the target model is a high-quality but computationally expensive diffusion model. We propose various drafting strategies, including a simple and effective approach that does not require training a draft model and is applicable out of the box to any diffusion model. Our experiments demonstrate significant generation speedup on various diffusion models, halving the number of function evaluations, while generating exact samples from the target model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge