Density Ratio-based Proxy Causal Learning Without Density Ratios

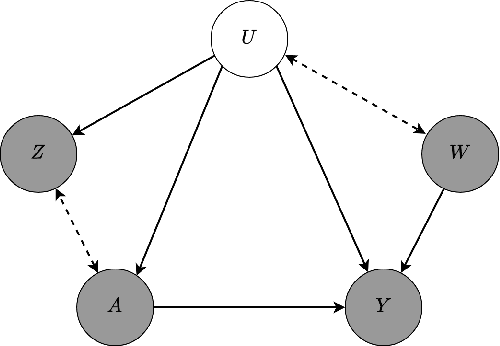
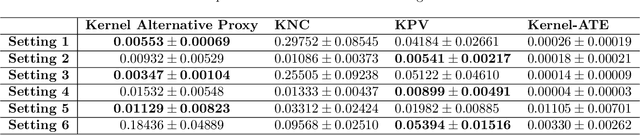
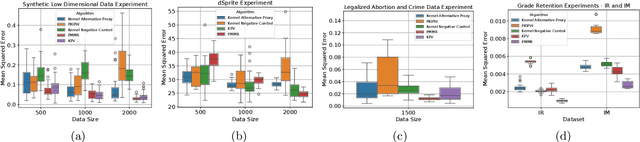
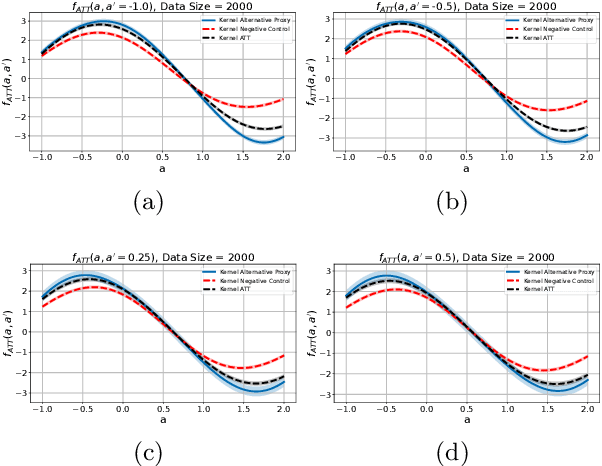
We address the setting of Proxy Causal Learning (PCL), which has the goal of estimating causal effects from observed data in the presence of hidden confounding. Proxy methods accomplish this task using two proxy variables related to the latent confounder: a treatment proxy (related to the treatment) and an outcome proxy (related to the outcome). Two approaches have been proposed to perform causal effect estimation given proxy variables; however only one of these has found mainstream acceptance, since the other was understood to require density ratio estimation - a challenging task in high dimensions. In the present work, we propose a practical and effective implementation of the second approach, which bypasses explicit density ratio estimation and is suitable for continuous and high-dimensional treatments. We employ kernel ridge regression to derive estimators, resulting in simple closed-form solutions for dose-response and conditional dose-response curves, along with consistency guarantees. Our methods empirically demonstrate superior or comparable performance to existing frameworks on synthetic and real-world datasets.

Many Proxy Controls

A recent literature considers causal inference using noisy proxies for unobserved confounding factors. The proxies are divided into two sets that are independent conditional on the confounders. One set of proxies are `negative control treatments' and the other are `negative control outcomes'. Existing work applies to low-dimensional settings with a fixed number of proxies and confounders. In this work we consider linear models with many proxy controls and possibly many confounders. A key insight is that if each group of proxies is strictly larger than the number of confounding factors, then a matrix of nuisance parameters has a low-rank structure and a vector of nuisance parameters has a sparse structure. We can exploit the rank-restriction and sparsity to reduce the number of free parameters to be estimated. The number of unobserved confounders is not known a priori but we show that it is identified, and we apply penalization methods to adapt to this quantity. We provide an estimator with a closed-form as well as a doubly-robust estimator that must be evaluated using numerical methods. We provide conditions under which our doubly-robust estimator is uniformly root-$n$ consistent, asymptotically centered normal, and our suggested confidence intervals have asymptotically correct coverage. We provide simulation evidence that our methods achieve better performance than existing approaches in high dimensions, particularly when the number of proxies is substantially larger than the number of confounders.