Kernel Single Proxy Control for Deterministic Confounding

We consider the problem of causal effect estimation with an unobserved confounder, where we observe a proxy variable that is associated with the confounder. Although Proxy Causal Learning (PCL) uses two proxy variables to recover the true causal effect, we show that a single proxy variable is sufficient for causal estimation if the outcome is generated deterministically, generalizing Control Outcome Calibration Approach (COCA). We propose two kernel-based methods for this setting: the first based on the two-stage regression approach, and the second based on a maximum moment restriction approach. We prove that both approaches can consistently estimate the causal effect, and we empirically demonstrate that we can successfully recover the causal effect on a synthetic dataset.

A Neural Mean Embedding Approach for Back-door and Front-door Adjustment

We consider the estimation of average and counterfactual treatment effects, under two settings: back-door adjustment and front-door adjustment. The goal in both cases is to recover the treatment effect without having an access to a hidden confounder. This objective is attained by first estimating the conditional mean of the desired outcome variable given relevant covariates (the "first stage" regression), and then taking the (conditional) expectation of this function as a "second stage" procedure. We propose to compute these conditional expectations directly using a regression function to the learned input features of the first stage, thus avoiding the need for sampling or density estimation. All functions and features (and in particular, the output features in the second stage) are neural networks learned adaptively from data, with the sole requirement that the final layer of the first stage should be linear. The proposed method is shown to converge to the true causal parameter, and outperforms the recent state-of-the-art methods on challenging causal benchmarks, including settings involving high-dimensional image data.

Importance Weighting Approach in Kernel Bayes' Rule

We study a nonparametric approach to Bayesian computation via feature means, where the expectation of prior features is updated to yield expected posterior features, based on regression from kernel or neural net features of the observations. All quantities involved in the Bayesian update are learned from observed data, making the method entirely model-free. The resulting algorithm is a novel instance of a kernel Bayes' rule (KBR). Our approach is based on importance weighting, which results in superior numerical stability to the existing approach to KBR, which requires operator inversion. We show the convergence of the estimator using a novel consistency analysis on the importance weighting estimator in the infinity norm. We evaluate our KBR on challenging synthetic benchmarks, including a filtering problem with a state-space model involving high dimensional image observations. The proposed method yields uniformly better empirical performance than the existing KBR, and competitive performance with other competing methods.

Kernel Methods for Multistage Causal Inference: Mediation Analysis and Dynamic Treatment Effects

We propose kernel ridge regression estimators for mediation analysis and dynamic treatment effects over short horizons. We allow treatments, covariates, and mediators to be discrete or continuous, and low, high, or infinite dimensional. We propose estimators of means, increments, and distributions of counterfactual outcomes with closed form solutions in terms of kernel matrix operations. For the continuous treatment case, we prove uniform consistency with finite sample rates. For the discrete treatment case, we prove root-n consistency, Gaussian approximation, and semiparametric efficiency. We conduct simulations then estimate mediated and dynamic treatment effects of the US Job Corps program for disadvantaged youth.

Deep Proxy Causal Learning and its Application to Confounded Bandit Policy Evaluation

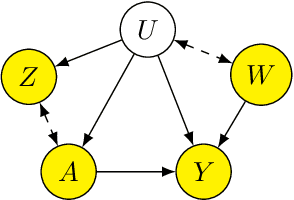
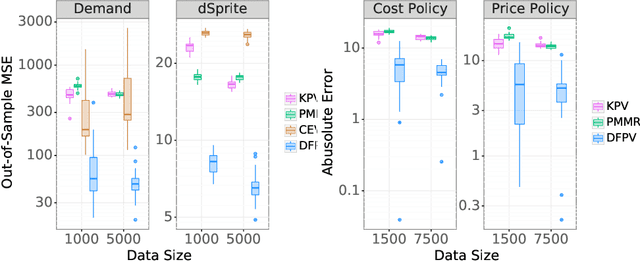
Proxy causal learning (PCL) is a method for estimating the causal effect of treatments on outcomes in the presence of unobserved confounding, using proxies (structured side information) for the confounder. This is achieved via two-stage regression: in the first stage, we model relations among the treatment and proxies; in the second stage, we use this model to learn the effect of treatment on the outcome, given the context provided by the proxies. PCL guarantees recovery of the true causal effect, subject to identifiability conditions. We propose a novel method for PCL, the deep feature proxy variable method (DFPV), to address the case where the proxies, treatments, and outcomes are high-dimensional and have nonlinear complex relationships, as represented by deep neural network features. We show that DFPV outperforms recent state-of-the-art PCL methods on challenging synthetic benchmarks, including settings involving high dimensional image data. Furthermore, we show that PCL can be applied to off-policy evaluation for the confounded bandit problem, in which DFPV also exhibits competitive performance.

On Instrumental Variable Regression for Deep Offline Policy Evaluation

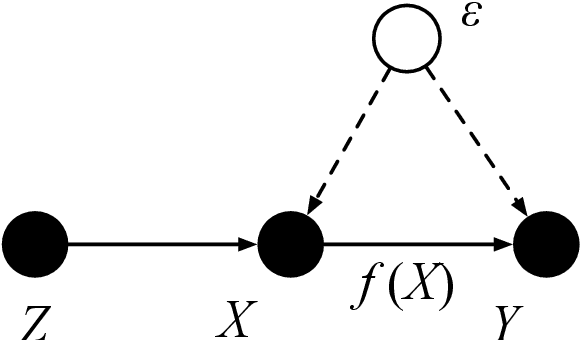
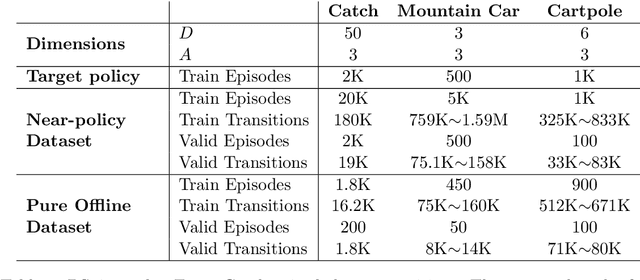
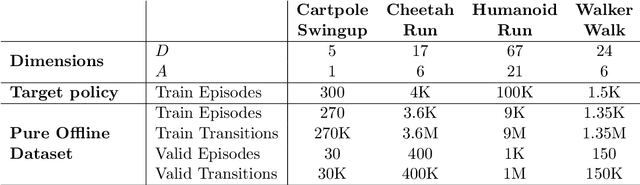
We show that the popular reinforcement learning (RL) strategy of estimating the state-action value (Q-function) by minimizing the mean squared Bellman error leads to a regression problem with confounding, the inputs and output noise being correlated. Hence, direct minimization of the Bellman error can result in significantly biased Q-function estimates. We explain why fixing the target Q-network in Deep Q-Networks and Fitted Q Evaluation provides a way of overcoming this confounding, thus shedding new light on this popular but not well understood trick in the deep RL literature. An alternative approach to address confounding is to leverage techniques developed in the causality literature, notably instrumental variables (IV). We bring together here the literature on IV and RL by investigating whether IV approaches can lead to improved Q-function estimates. This paper analyzes and compares a wide range of recent IV methods in the context of offline policy evaluation (OPE), where the goal is to estimate the value of a policy using logged data only. By applying different IV techniques to OPE, we are not only able to recover previously proposed OPE methods such as model-based techniques but also to obtain competitive new techniques. We find empirically that state-of-the-art OPE methods are closely matched in performance by some IV methods such as AGMM, which were not developed for OPE. We open-source all our code and datasets at https://github.com/liyuan9988/IVOPEwithACME.

Learning Deep Features in Instrumental Variable Regression

Instrumental variable (IV) regression is a standard strategy for learning causal relationships between confounded treatment and outcome variables from observational data by utilizing an instrumental variable, which affects the outcome only through the treatment. In classical IV regression, learning proceeds in two stages: stage 1 performs linear regression from the instrument to the treatment; and stage 2 performs linear regression from the treatment to the outcome, conditioned on the instrument. We propose a novel method, deep feature instrumental variable regression (DFIV), to address the case where relations between instruments, treatments, and outcomes may be nonlinear. In this case, deep neural nets are trained to define informative nonlinear features on the instruments and treatments. We propose an alternating training regime for these features to ensure good end-to-end performance when composing stages 1 and 2, thus obtaining highly flexible feature maps in a computationally efficient manner. DFIV outperforms recent state-of-the-art methods on challenging IV benchmarks, including settings involving high dimensional image data. DFIV also exhibits competitive performance in off-policy policy evaluation for reinforcement learning, which can be understood as an IV regression task.

Kernel Methods for Policy Evaluation: Treatment Effects, Mediation Analysis, and Off-Policy Planning

We propose a novel framework for non-parametric policy evaluation in static and dynamic settings. Under the assumption of selection on observables, we consider treatment effects of the population, of sub-populations, and of alternative populations that may have alternative covariate distributions. We further consider the decomposition of a total effect into a direct effect and an indirect effect (as mediated by a particular mechanism). Under the assumption of sequential selection on observables, we consider the effects of sequences of treatments. Across settings, we allow for treatments that may be discrete, continuous, or even text. Across settings, we allow for estimation of not only counterfactual mean outcomes but also counterfactual distributions of outcomes. We unify analyses across settings by showing that all of these causal learning problems reduce to the re-weighting of a prediction, i.e. causal adjustment. We implement the re-weighting as an inner product in a function space called a reproducing kernel Hilbert space (RKHS), with a closed form solution that can be computed in one line of code. We prove uniform consistency and provide finite sample rates of convergence. We evaluate our estimators in simulations devised by other authors. We use our new estimators to evaluate continuous and heterogeneous treatment effects of the US Jobs Corps training program for disadvantaged youth.

Similarity-based Classification: Connecting Similarity Learning to Binary Classification

In real-world classification problems, pairwise supervision (i.e., a pair of patterns with a binary label indicating whether they belong to the same class or not) can often be obtained at a lower cost than ordinary class labels. Similarity learning is a general framework to utilize such pairwise supervision to elicit useful representations by inferring the relationship between two data points, which encompasses various important preprocessing tasks such as metric learning, kernel learning, graph embedding, and contrastive representation learning. Although elicited representations are expected to perform well in downstream tasks such as classification, little theoretical insight has been given in the literature so far. In this paper, we reveal that a specific formulation of similarity learning is strongly related to the objective of binary classification, which spurs us to learn a binary classifier without ordinary class labels---by fitting the product of real-valued prediction functions of pairwise patterns to their similarity. Our formulation of similarity learning does not only generalize many existing ones, but also admits an excess risk bound showing an explicit connection to classification. Finally, we empirically demonstrate the practical usefulness of the proposed method on benchmark datasets.

Uncoupled Regression from Pairwise Comparison Data

Uncoupled regression is the problem to learn a model from unlabeled data and the set of target values while the correspondence between them is unknown. Such a situation arises in predicting anonymized targets that involve sensitive information, e.g., one's annual income. Since existing methods for uncoupled regression often require strong assumptions on the true target function, and thus, their range of applications is limited, we introduce a novel framework that does not require such assumptions in this paper. Our key idea is to utilize pairwise comparison data, which consists of pairs of unlabeled data that we know which one has a larger target value. Such pairwise comparison data is easy to collect, as typically discussed in the learning-to-rank scenario, and does not break the anonymity of data. We propose two practical methods for uncoupled regression from pairwise comparison data and show that the learned regression model converges to the optimal model with the optimal parametric convergence rate when the target variable distributes uniformly. Moreover, we empirically show that for linear models the proposed methods are comparable to ordinary supervised regression with labeled data.