Similarity-based Classification: Connecting Similarity Learning to Binary Classification

In real-world classification problems, pairwise supervision (i.e., a pair of patterns with a binary label indicating whether they belong to the same class or not) can often be obtained at a lower cost than ordinary class labels. Similarity learning is a general framework to utilize such pairwise supervision to elicit useful representations by inferring the relationship between two data points, which encompasses various important preprocessing tasks such as metric learning, kernel learning, graph embedding, and contrastive representation learning. Although elicited representations are expected to perform well in downstream tasks such as classification, little theoretical insight has been given in the literature so far. In this paper, we reveal that a specific formulation of similarity learning is strongly related to the objective of binary classification, which spurs us to learn a binary classifier without ordinary class labels---by fitting the product of real-valued prediction functions of pairwise patterns to their similarity. Our formulation of similarity learning does not only generalize many existing ones, but also admits an excess risk bound showing an explicit connection to classification. Finally, we empirically demonstrate the practical usefulness of the proposed method on benchmark datasets.

Data Interpolating Prediction: Alternative Interpretation of Mixup

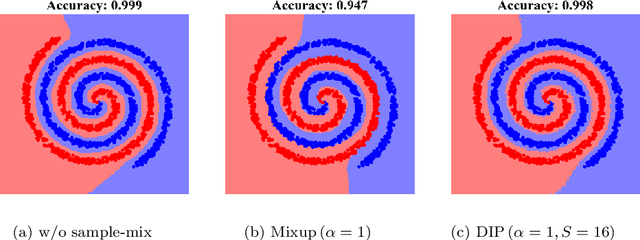
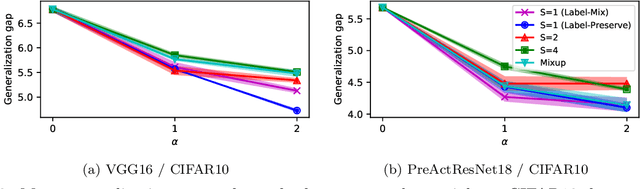
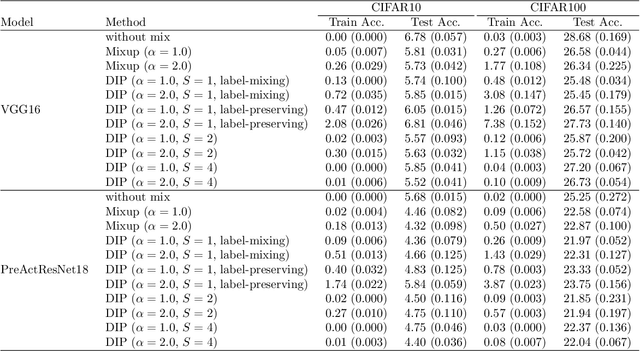
Data augmentation by mixing samples, such as Mixup, has widely been used typically for classification tasks. However, this strategy is not always effective due to the gap between augmented samples for training and original samples for testing. This gap may prevent a classifier from learning the optimal decision boundary and increase the generalization error. To overcome this problem, we propose an alternative framework called Data Interpolating Prediction (DIP). Unlike common data augmentations, we encapsulate the sample-mixing process in the hypothesis class of a classifier so that train and test samples are treated equally. We derive the generalization bound and show that DIP helps to reduce the original Rademacher complexity. Also, we empirically demonstrate that DIP can outperform existing Mixup.

Classification from Pairwise Similarities/Dissimilarities and Unlabeled Data via Empirical Risk Minimization

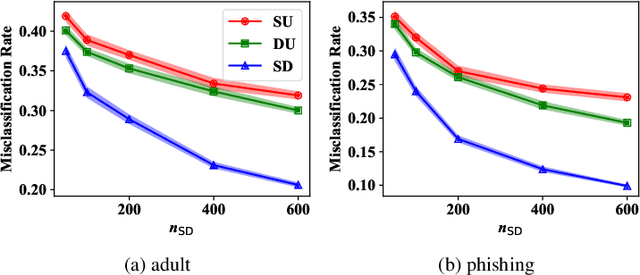
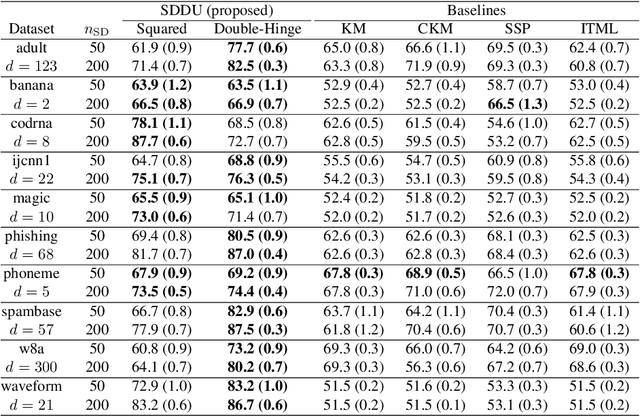
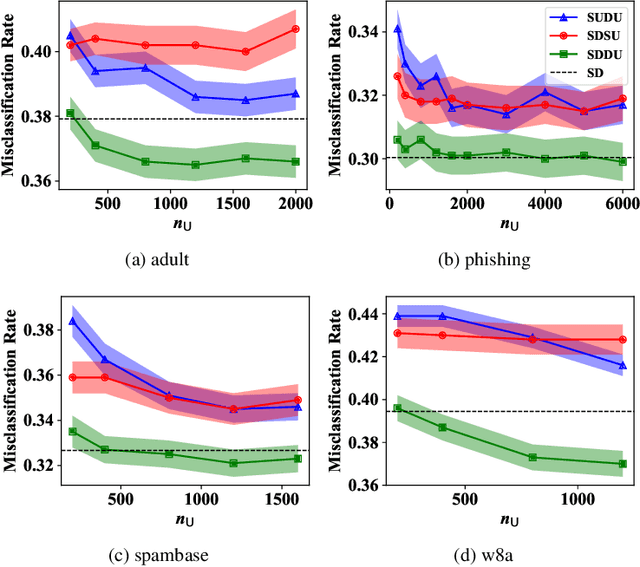
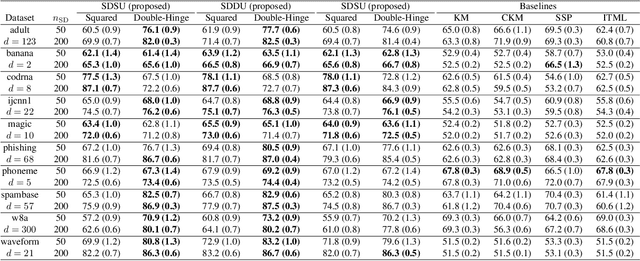
Pairwise similarities and dissimilarities between data points might be easier to obtain than fully labeled data in real-world classification problems, e.g., in privacy-aware situations. To handle such pairwise information, an empirical risk minimization approach has been proposed, giving an unbiased estimator of the classification risk that can be computed only from pairwise similarities and unlabeled data. However, this direction cannot handle pairwise dissimilarities so far. On the other hand, semi-supervised clustering is one of the methods which can use both similarities and dissimilarities. Nevertheless, they typically require strong geometrical assumptions on the data distribution such as the manifold assumption, which may deteriorate the performance. In this paper, we derive an unbiased risk estimator which can handle all of similarities/dissimilarities and unlabeled data. We theoretically establish estimation error bounds and experimentally demonstrate the practical usefulness of our empirical risk minimization method.