Classification from Pairwise Similarities/Dissimilarities and Unlabeled Data via Empirical Risk Minimization
Paper and Code
Apr 26, 2019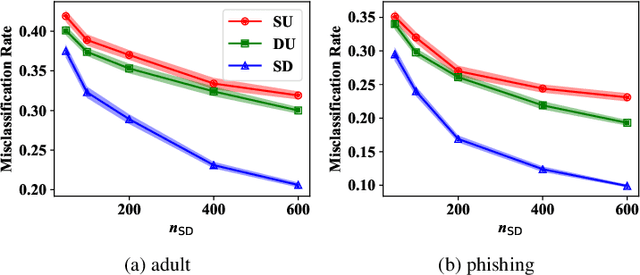
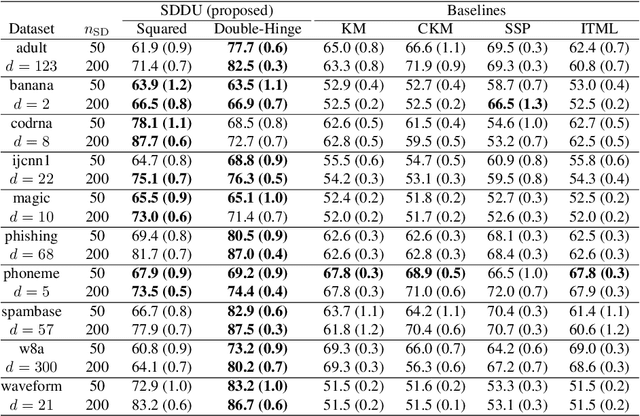
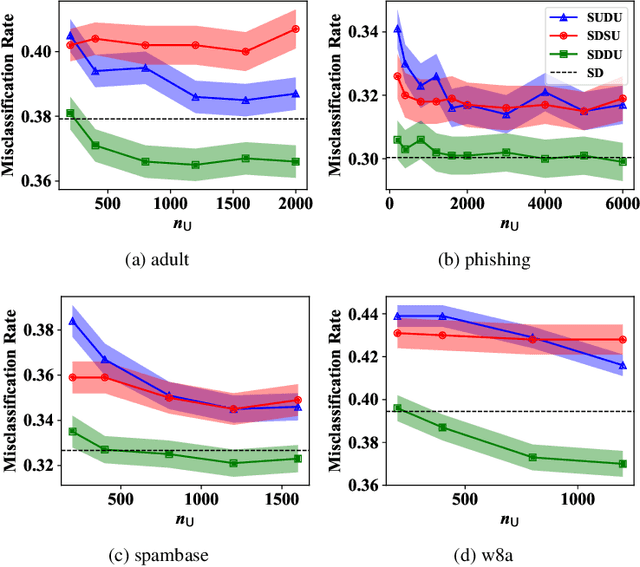
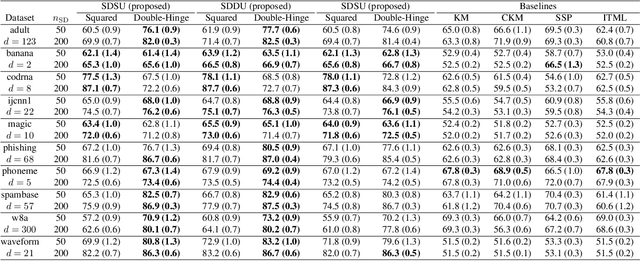
Pairwise similarities and dissimilarities between data points might be easier to obtain than fully labeled data in real-world classification problems, e.g., in privacy-aware situations. To handle such pairwise information, an empirical risk minimization approach has been proposed, giving an unbiased estimator of the classification risk that can be computed only from pairwise similarities and unlabeled data. However, this direction cannot handle pairwise dissimilarities so far. On the other hand, semi-supervised clustering is one of the methods which can use both similarities and dissimilarities. Nevertheless, they typically require strong geometrical assumptions on the data distribution such as the manifold assumption, which may deteriorate the performance. In this paper, we derive an unbiased risk estimator which can handle all of similarities/dissimilarities and unlabeled data. We theoretically establish estimation error bounds and experimentally demonstrate the practical usefulness of our empirical risk minimization method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge