VModA: An Effective Framework for Adaptive NSFW Image Moderation

Not Safe/Suitable for Work (NSFW) content is rampant on social networks and poses serious harm to citizens, especially minors. Current detection methods mainly rely on deep learning-based image recognition and classification. However, NSFW images are now presented in increasingly sophisticated ways, often using image details and complex semantics to obscure their true nature or attract more views. Although still understandable to humans, these images often evade existing detection methods, posing a significant threat. Further complicating the issue, varying regulations across platforms and regions create additional challenges for effective moderation, leading to detection bias and reduced accuracy. To address this, we propose VModA, a general and effective framework that adapts to diverse moderation rules and handles complex, semantically rich NSFW content across categories. Experimental results show that VModA significantly outperforms existing methods, achieving up to a 54.3% accuracy improvement across NSFW types, including those with complex semantics. Further experiments demonstrate that our method exhibits strong adaptability across categories, scenarios, and base VLMs. We also identified inconsistent and controversial label samples in public NSFW benchmark datasets, re-annotated them, and submitted corrections to the original maintainers. Two datasets have confirmed the updates so far. Additionally, we evaluate VModA in real-world scenarios to demonstrate its practical effectiveness.

MentalMAC: Enhancing Large Language Models for Detecting Mental Manipulation via Multi-Task Anti-Curriculum Distillation

Mental manipulation is a subtle yet pervasive form of psychological abuse that poses serious threats to mental health. Its covert nature and the complexity of manipulation strategies make it challenging to detect, even for state-of-the-art large language models (LLMs). This concealment also hinders the manual collection of large-scale, high-quality annotations essential for training effective models. Although recent efforts have sought to improve LLM's performance on this task, progress remains limited due to the scarcity of real-world annotated datasets. To address these challenges, we propose MentalMAC, a multi-task anti-curriculum distillation method that enhances LLMs' ability to detect mental manipulation in multi-turn dialogue. Our approach includes: (i) EvoSA, an unsupervised data expansion method based on evolutionary operations and speech act theory; (ii) teacher-model-generated multi-task supervision; and (iii) progressive knowledge distillation from complex to simpler tasks. We then constructed the ReaMent dataset with 5,000 real-world dialogue samples, using a MentalMAC-distilled model to assist human annotation. Vast experiments demonstrate that our method significantly narrows the gap between student and teacher models and outperforms competitive LLMs across key evaluation metrics. All code, datasets, and checkpoints will be released upon paper acceptance. Warning: This paper contains content that may be offensive to readers.

Establishing Linear Surrogate Regret Bounds for Convex Smooth Losses via Convolutional Fenchel-Young Losses

Surrogate regret bounds, also known as excess risk bounds, bridge the gap between the convergence rates of surrogate and target losses, with linear bounds favorable for their lossless regret transfer. While convex smooth surrogate losses are appealing in particular due to the efficient estimation and optimization, the existence of a trade-off between the smoothness and linear regret bound has been believed in the community. That being said, the better optimization and estimation properties of convex smooth surrogate losses may inevitably deteriorate after undergoing the regret transfer onto a target loss. We overcome this dilemma for arbitrary discrete target losses by constructing a convex smooth surrogate loss, which entails a linear surrogate regret bound composed with a tailored prediction link. The construction is based on Fenchel-Young losses generated by the convolutional negentropy, which are equivalent to the infimal convolution of a generalized negentropy and the target Bayes risk. Consequently, the infimal convolution enables us to derive a smooth loss while maintaining the surrogate regret bound linear. We additionally benefit from the infimal convolution to have a consistent estimator of the underlying class probability. Our results are overall a novel demonstration of how convex analysis penetrates into optimization and statistical efficiency in risk minimization.

Many-to-Many Matching via Sparsity Controlled Optimal Transport

Many-to-many matching seeks to match multiple points in one set and multiple points in another set, which is a basis for a wide range of data mining problems. It can be naturally recast in the framework of Optimal Transport (OT). However, existing OT methods either lack the ability to accomplish many-to-many matching or necessitate careful tuning of a regularization parameter to achieve satisfactory results. This paper proposes a novel many-to-many matching method to explicitly encode many-to-many constraints while preventing the degeneration into one-to-one matching. The proposed method consists of the following two components. The first component is the matching budget constraints on each row and column of a transport plan, which specify how many points can be matched to a point at most. The second component is the deformed $q$-entropy regularization, which encourages a point to meet the matching budget maximally. While the deformed $q$-entropy was initially proposed to sparsify a transport plan, we employ it to avoid the degeneration into one-to-one matching. We optimize the objective via a penalty algorithm, which is efficient and theoretically guaranteed to converge. Experimental results on various tasks demonstrate that the proposed method achieves good performance by gleaning meaningful many-to-many matchings.

Any-stepsize Gradient Descent for Separable Data under Fenchel--Young Losses

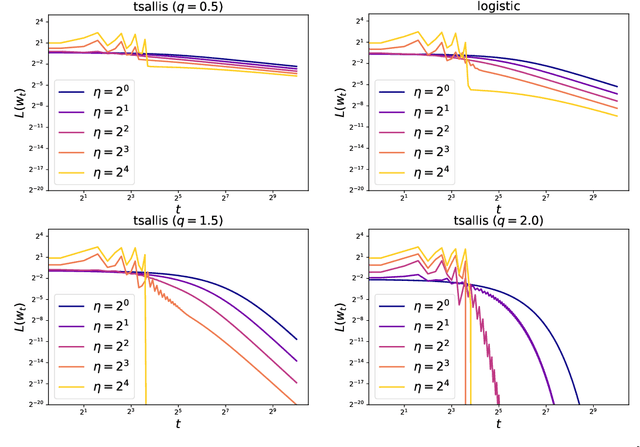
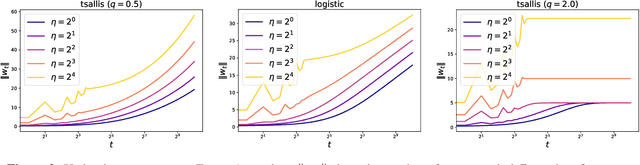
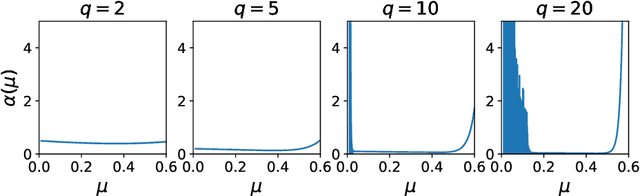
The gradient descent (GD) has been one of the most common optimizer in machine learning. In particular, the loss landscape of a neural network is typically sharpened during the initial phase of training, making the training dynamics hover on the edge of stability. This is beyond our standard understanding of GD convergence in the stable regime where arbitrarily chosen stepsize is sufficiently smaller than the edge of stability. Recently, Wu et al. (COLT2024) have showed that GD converges with arbitrary stepsize under linearly separable logistic regression. Although their analysis hinges on the self-bounding property of the logistic loss, which seems to be a cornerstone to establish a modified descent lemma, our pilot study shows that other loss functions without the self-bounding property can make GD converge with arbitrary stepsize. To further understand what property of a loss function matters in GD, we aim to show arbitrary-stepsize GD convergence for a general loss function based on the framework of \emph{Fenchel--Young losses}. We essentially leverage the classical perceptron argument to derive the convergence rate for achieving $\epsilon$-optimal loss, which is possible for a majority of Fenchel--Young losses. Among typical loss functions, the Tsallis entropy achieves the GD convergence rate $T=\Omega(\epsilon^{-1/2})$, and the R{\'e}nyi entropy achieves the far better rate $T=\Omega(\epsilon^{-1/3})$. We argue that these better rate is possible because of \emph{separation margin} of loss functions, instead of the self-bounding property.

TAID: Temporally Adaptive Interpolated Distillation for Efficient Knowledge Transfer in Language Models

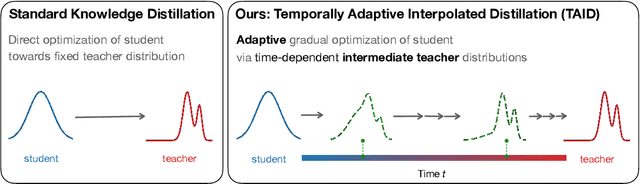
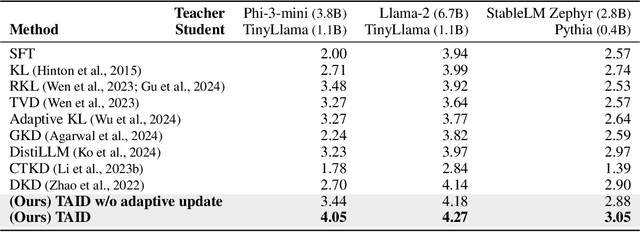
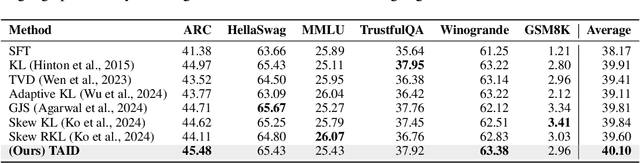
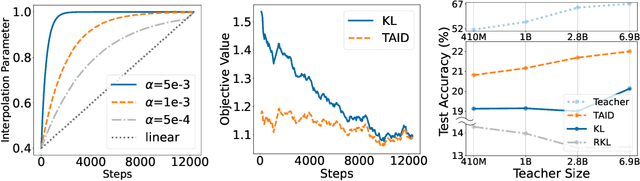
Causal language models have demonstrated remarkable capabilities, but their size poses significant challenges for deployment in resource-constrained environments. Knowledge distillation, a widely-used technique for transferring knowledge from a large teacher model to a small student model, presents a promising approach for model compression. A significant remaining issue lies in the major differences between teacher and student models, namely the substantial capacity gap, mode averaging, and mode collapse, which pose barriers during distillation. To address these issues, we introduce $\textit{Temporally Adaptive Interpolated Distillation (TAID)}$, a novel knowledge distillation approach that dynamically interpolates student and teacher distributions through an adaptive intermediate distribution, gradually shifting from the student's initial distribution towards the teacher's distribution. We provide a theoretical analysis demonstrating TAID's ability to prevent mode collapse and empirically show its effectiveness in addressing the capacity gap while balancing mode averaging and mode collapse. Our comprehensive experiments demonstrate TAID's superior performance across various model sizes and architectures in both instruction tuning and pre-training scenarios. Furthermore, we showcase TAID's practical impact by developing two state-of-the-art compact foundation models: $\texttt{TAID-LLM-1.5B}$ for language tasks and $\texttt{TAID-VLM-2B}$ for vision-language tasks. These results demonstrate TAID's effectiveness in creating high-performing and efficient models, advancing the development of more accessible AI technologies.

Online Inverse Linear Optimization: Improved Regret Bound, Robustness to Suboptimality, and Toward Tight Regret Analysis

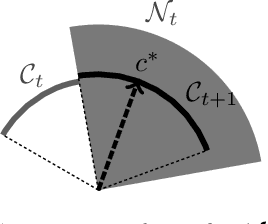
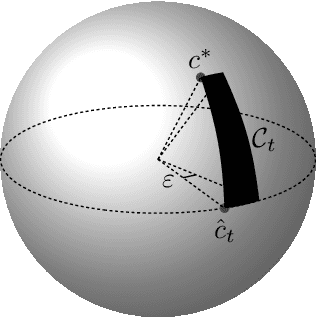
We study an online learning problem where, over $T$ rounds, a learner observes both time-varying sets of feasible actions and an agent's optimal actions, selected by solving linear optimization over the feasible actions. The learner sequentially makes predictions of the agent's underlying linear objective function, and their quality is measured by the regret, the cumulative gap between optimal objective values and those achieved by following the learner's predictions. A seminal work by B\"armann et al. (ICML 2017) showed that online learning methods can be applied to this problem to achieve regret bounds of $O(\sqrt{T})$. Recently, Besbes et al. (COLT 2021, Oper. Res. 2023) significantly improved the result by achieving an $O(n^4\ln T)$ regret bound, where $n$ is the dimension of the ambient space of objective vectors. Their method, based on the ellipsoid method, runs in polynomial time but is inefficient for large $n$ and $T$. In this paper, we obtain an $O(n\ln T)$ regret bound, improving upon the previous bound of $O(n^4\ln T)$ by a factor of $n^3$. Our method is simple and efficient: we apply the online Newton step (ONS) to appropriate exp-concave loss functions. Moreover, for the case where the agent's actions are possibly suboptimal, we establish an $O(n\ln T+\sqrt{\Delta_Tn\ln T})$ regret bound, where $\Delta_T$ is the cumulative suboptimality of the agent's actions. This bound is achieved by using MetaGrad, which runs ONS with $\Theta(\ln T)$ different learning rates in parallel. We also provide a simple instance that implies an $\Omega(n)$ lower bound, showing that our $O(n\ln T)$ bound is tight up to an $O(\ln T)$ factor. This gives rise to a natural question: can the $O(\ln T)$ factor in the upper bound be removed? For the special case of $n=2$, we show that an $O(1)$ regret bound is possible, while we delineate challenges in extending this result to higher dimensions.

Revisiting Online Learning Approach to Inverse Linear Optimization: A Fenchel$-$Young Loss Perspective and Gap-Dependent Regret Analysis

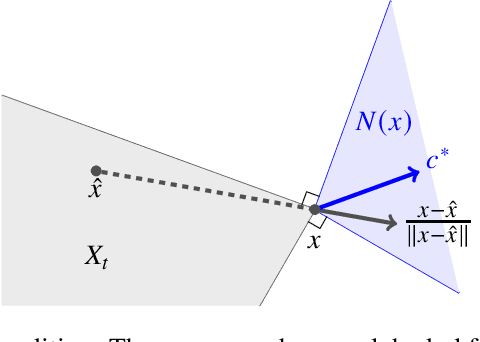
This paper revisits the online learning approach to inverse linear optimization studied by B\"armann et al. (2017), where the goal is to infer an unknown linear objective function of an agent from sequential observations of the agent's input-output pairs. First, we provide a simple understanding of the online learning approach through its connection to online convex optimization of \emph{Fenchel--Young losses}. As a byproduct, we present an offline guarantee on the \emph{suboptimality loss}, which measures how well predicted objectives explain the agent's choices, without assuming the optimality of the agent's choices. Second, assuming that there is a gap between optimal and suboptimal objective values in the agent's decision problems, we obtain an upper bound independent of the time horizon $T$ on the sum of suboptimality and \emph{estimate losses}, where the latter measures the quality of solutions recommended by predicted objectives. Interestingly, our gap-dependent analysis achieves a faster rate than the standard $O(\sqrt{T})$ regret bound by exploiting structures specific to inverse linear optimization, even though neither the loss functions nor their domains enjoy desirable properties, such as strong convexity.

DeepSeek-V3 Technical Report

We present DeepSeek-V3, a strong Mixture-of-Experts (MoE) language model with 671B total parameters with 37B activated for each token. To achieve efficient inference and cost-effective training, DeepSeek-V3 adopts Multi-head Latent Attention (MLA) and DeepSeekMoE architectures, which were thoroughly validated in DeepSeek-V2. Furthermore, DeepSeek-V3 pioneers an auxiliary-loss-free strategy for load balancing and sets a multi-token prediction training objective for stronger performance. We pre-train DeepSeek-V3 on 14.8 trillion diverse and high-quality tokens, followed by Supervised Fine-Tuning and Reinforcement Learning stages to fully harness its capabilities. Comprehensive evaluations reveal that DeepSeek-V3 outperforms other open-source models and achieves performance comparable to leading closed-source models. Despite its excellent performance, DeepSeek-V3 requires only 2.788M H800 GPU hours for its full training. In addition, its training process is remarkably stable. Throughout the entire training process, we did not experience any irrecoverable loss spikes or perform any rollbacks. The model checkpoints are available at https://github.com/deepseek-ai/DeepSeek-V3.

Zipfian Whitening

The word embedding space in neural models is skewed, and correcting this can improve task performance. We point out that most approaches for modeling, correcting, and measuring the symmetry of an embedding space implicitly assume that the word frequencies are uniform; in reality, word frequencies follow a highly non-uniform distribution, known as Zipf's law. Surprisingly, simply performing PCA whitening weighted by the empirical word frequency that follows Zipf's law significantly improves task performance, surpassing established baselines. From a theoretical perspective, both our approach and existing methods can be clearly categorized: word representations are distributed according to an exponential family with either uniform or Zipfian base measures. By adopting the latter approach, we can naturally emphasize informative low-frequency words in terms of their vector norm, which becomes evident from the information-geometric perspective, and in terms of the loss functions for imbalanced classification. Additionally, our theory corroborates that popular natural language processing methods, such as skip-gram negative sampling, WhiteningBERT, and headless language models, work well just because their word embeddings encode the empirical word frequency into the underlying probabilistic model.