Any-stepsize Gradient Descent for Separable Data under Fenchel--Young Losses
Paper and Code
Feb 07, 2025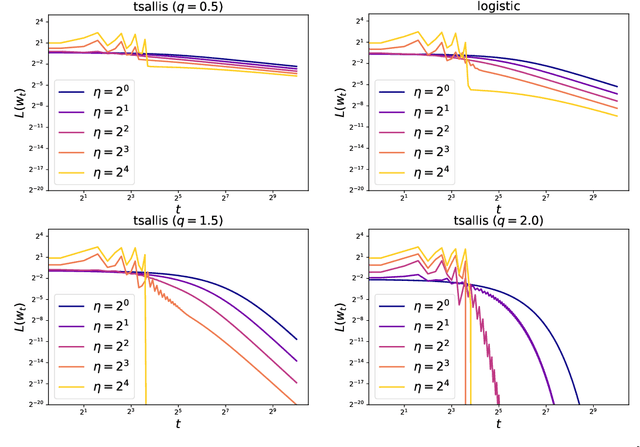

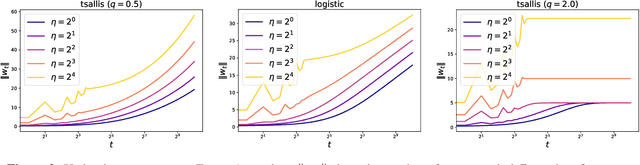
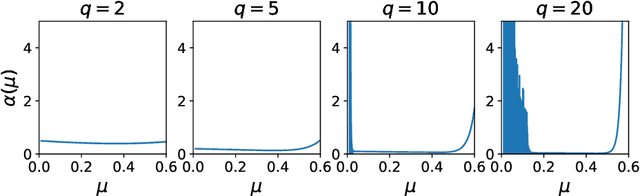
The gradient descent (GD) has been one of the most common optimizer in machine learning. In particular, the loss landscape of a neural network is typically sharpened during the initial phase of training, making the training dynamics hover on the edge of stability. This is beyond our standard understanding of GD convergence in the stable regime where arbitrarily chosen stepsize is sufficiently smaller than the edge of stability. Recently, Wu et al. (COLT2024) have showed that GD converges with arbitrary stepsize under linearly separable logistic regression. Although their analysis hinges on the self-bounding property of the logistic loss, which seems to be a cornerstone to establish a modified descent lemma, our pilot study shows that other loss functions without the self-bounding property can make GD converge with arbitrary stepsize. To further understand what property of a loss function matters in GD, we aim to show arbitrary-stepsize GD convergence for a general loss function based on the framework of \emph{Fenchel--Young losses}. We essentially leverage the classical perceptron argument to derive the convergence rate for achieving $\epsilon$-optimal loss, which is possible for a majority of Fenchel--Young losses. Among typical loss functions, the Tsallis entropy achieves the GD convergence rate $T=\Omega(\epsilon^{-1/2})$, and the R{\'e}nyi entropy achieves the far better rate $T=\Omega(\epsilon^{-1/3})$. We argue that these better rate is possible because of \emph{separation margin} of loss functions, instead of the self-bounding property.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge