Yuki Takezawa
Exploiting Similarity for Computation and Communication-Efficient Decentralized Optimization
Jun 06, 2025Abstract:Reducing communication complexity is critical for efficient decentralized optimization. The proximal decentralized optimization (PDO) framework is particularly appealing, as methods within this framework can exploit functional similarity among nodes to reduce communication rounds. Specifically, when local functions at different nodes are similar, these methods achieve faster convergence with fewer communication steps. However, existing PDO methods often require highly accurate solutions to subproblems associated with the proximal operator, resulting in significant computational overhead. In this work, we propose the Stabilized Proximal Decentralized Optimization (SPDO) method, which achieves state-of-the-art communication and computational complexities within the PDO framework. Additionally, we refine the analysis of existing PDO methods by relaxing subproblem accuracy requirements and leveraging average functional similarity. Experimental results demonstrate that SPDO significantly outperforms existing methods.
Any-stepsize Gradient Descent for Separable Data under Fenchel--Young Losses
Feb 07, 2025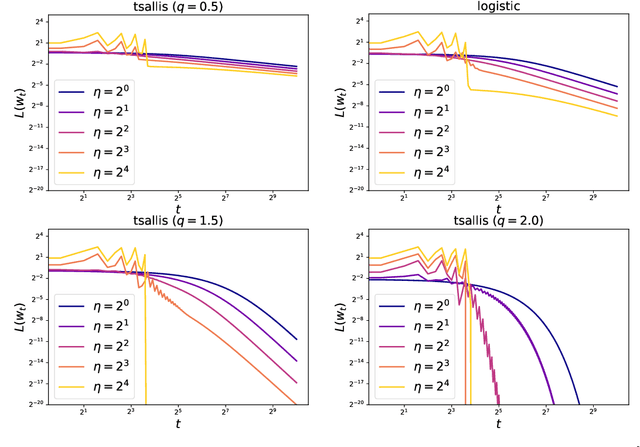

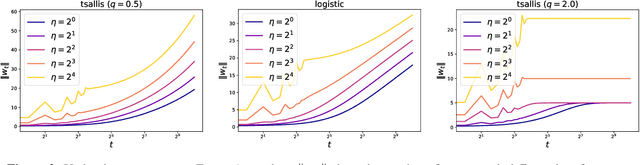
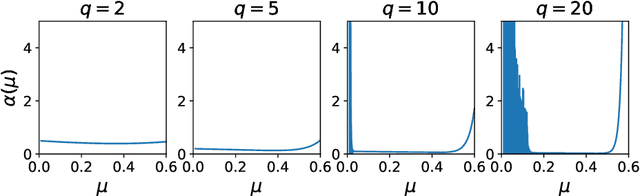
Abstract:The gradient descent (GD) has been one of the most common optimizer in machine learning. In particular, the loss landscape of a neural network is typically sharpened during the initial phase of training, making the training dynamics hover on the edge of stability. This is beyond our standard understanding of GD convergence in the stable regime where arbitrarily chosen stepsize is sufficiently smaller than the edge of stability. Recently, Wu et al. (COLT2024) have showed that GD converges with arbitrary stepsize under linearly separable logistic regression. Although their analysis hinges on the self-bounding property of the logistic loss, which seems to be a cornerstone to establish a modified descent lemma, our pilot study shows that other loss functions without the self-bounding property can make GD converge with arbitrary stepsize. To further understand what property of a loss function matters in GD, we aim to show arbitrary-stepsize GD convergence for a general loss function based on the framework of \emph{Fenchel--Young losses}. We essentially leverage the classical perceptron argument to derive the convergence rate for achieving $\epsilon$-optimal loss, which is possible for a majority of Fenchel--Young losses. Among typical loss functions, the Tsallis entropy achieves the GD convergence rate $T=\Omega(\epsilon^{-1/2})$, and the R{\'e}nyi entropy achieves the far better rate $T=\Omega(\epsilon^{-1/3})$. We argue that these better rate is possible because of \emph{separation margin} of loss functions, instead of the self-bounding property.
Scalable Decentralized Learning with Teleportation
Jan 25, 2025Abstract:Decentralized SGD can run with low communication costs, but its sparse communication characteristics deteriorate the convergence rate, especially when the number of nodes is large. In decentralized learning settings, communication is assumed to occur on only a given topology, while in many practical cases, the topology merely represents a preferred communication pattern, and connecting to arbitrary nodes is still possible. Previous studies have tried to alleviate the convergence rate degradation in these cases by designing topologies with large spectral gaps. However, the degradation is still significant when the number of nodes is substantial. In this work, we propose TELEPORTATION. TELEPORTATION activates only a subset of nodes, and the active nodes fetch the parameters from previous active nodes. Then, the active nodes update their parameters by SGD and perform gossip averaging on a relatively small topology comprising only the active nodes. We show that by activating only a proper number of nodes, TELEPORTATION can completely alleviate the convergence rate degradation. Furthermore, we propose an efficient hyperparameter-tuning method to search for the appropriate number of nodes to be activated. Experimentally, we showed that TELEPORTATION can train neural networks more stably and achieve higher accuracy than Decentralized SGD.
Polyak Meets Parameter-free Clipped Gradient Descent
May 23, 2024
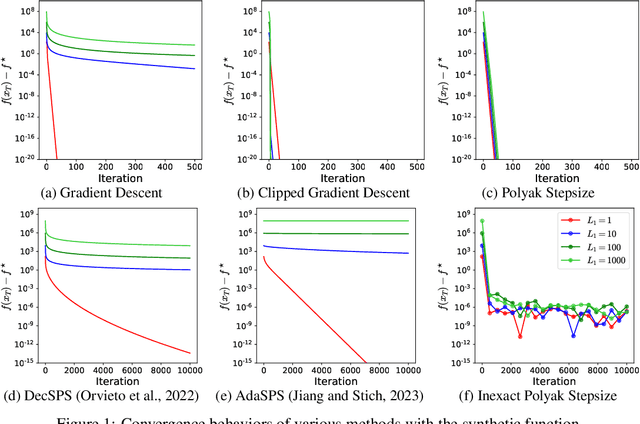
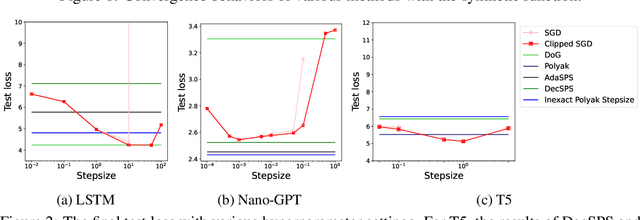
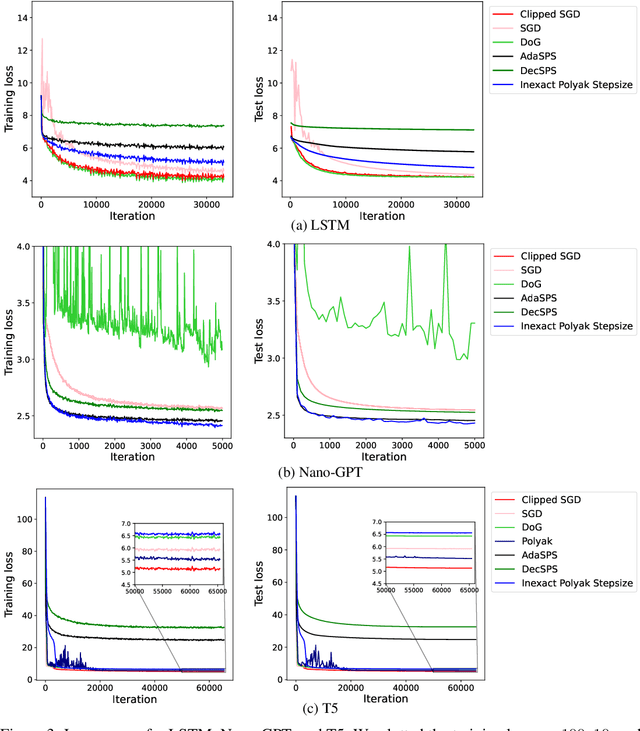
Abstract:Gradient descent and its variants are de facto standard algorithms for training machine learning models. As gradient descent is sensitive to its hyperparameters, we need to tune the hyperparameters carefully using a grid search, but it is time-consuming, especially when multiple hyperparameters exist. Recently, parameter-free methods that adjust the hyperparameters on the fly have been studied. However, the existing work only studied parameter-free methods for the stepsize, and parameter-free methods for other hyperparameters have not been explored. For instance, the gradient clipping threshold is also a crucial hyperparameter in addition to the stepsize to prevent gradient explosion issues, but none of the existing studies investigated the parameter-free methods for clipped gradient descent. In this work, we study the parameter-free methods for clipped gradient descent. Specifically, we propose Inexact Polyak Stepsize, which converges to the optimal solution without any hyperparameters tuning, and its convergence rate is asymptotically independent of L under L-smooth and $(L_0, L_1)$-smooth assumptions of the loss function as that of clipped gradient descent with well-tuned hyperparameters. We numerically validated our convergence results using a synthetic function and demonstrated the effectiveness of our proposed methods using LSTM, Nano-GPT, and T5.
PhiNets: Brain-inspired Non-contrastive Learning Based on Temporal Prediction Hypothesis
May 23, 2024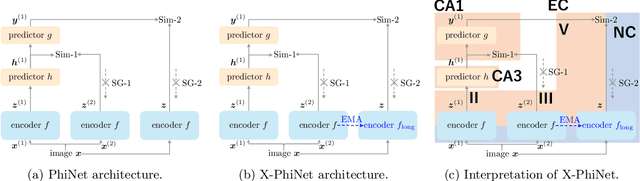

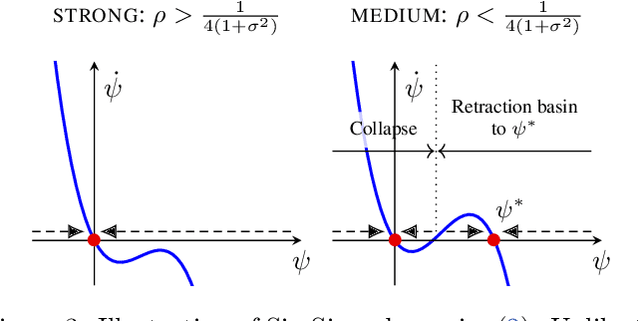
Abstract:SimSiam is a prominent self-supervised learning method that achieves impressive results in various vision tasks under static environments. However, it has two critical issues: high sensitivity to hyperparameters, especially weight decay, and unsatisfactory performance in online and continual learning, where neuroscientists believe that powerful memory functions are necessary, as in brains. In this paper, we propose PhiNet, inspired by a hippocampal model based on the temporal prediction hypothesis. Unlike SimSiam, which aligns two augmented views of the original image, PhiNet integrates an additional predictor block that estimates the original image representation to imitate the CA1 region in the hippocampus. Moreover, we model the neocortex inspired by the Complementary Learning Systems theory with a momentum encoder block as a slow learner, which works as long-term memory. We demonstrate through analysing the learning dynamics that PhiNet benefits from the additional predictor to prevent the complete collapse of learned representations, a notorious challenge in non-contrastive learning. This dynamics analysis may partially corroborate why this hippocampal model is biologically plausible. Experimental results demonstrate that PhiNet is more robust to weight decay and performs better than SimSiam in memory-intensive tasks like online and continual learning.
An Empirical Study of Simplicial Representation Learning with Wasserstein Distance
Oct 16, 2023Abstract:In this paper, we delve into the problem of simplicial representation learning utilizing the 1-Wasserstein distance on a tree structure (a.k.a., Tree-Wasserstein distance (TWD)), where TWD is defined as the L1 distance between two tree-embedded vectors. Specifically, we consider a framework for simplicial representation estimation employing a self-supervised learning approach based on SimCLR with a negative TWD as a similarity measure. In SimCLR, the cosine similarity with real-vector embeddings is often utilized; however, it has not been well studied utilizing L1-based measures with simplicial embeddings. A key challenge is that training the L1 distance is numerically challenging and often yields unsatisfactory outcomes, and there are numerous choices for probability models. Thus, this study empirically investigates a strategy for optimizing self-supervised learning with TWD and find a stable training procedure. More specifically, we evaluate the combination of two types of TWD (total variation and ClusterTree) and several simplicial models including the softmax function, the ArcFace probability model, and simplicial embedding. Moreover, we propose a simple yet effective Jeffrey divergence-based regularization method to stabilize the optimization. Through empirical experiments on STL10, CIFAR10, CIFAR100, and SVHN, we first found that the simple combination of softmax function and TWD can obtain significantly lower results than the standard SimCLR (non-simplicial model and cosine similarity). We found that the model performance depends on the combination of TWD and the simplicial model, and the Jeffrey divergence regularization usually helps model training. Finally, we inferred that the appropriate choice of combination of TWD and simplicial models outperformed cosine similarity based representation learning.
Embarrassingly Simple Text Watermarks
Oct 13, 2023



Abstract:We propose Easymark, a family of embarrassingly simple yet effective watermarks. Text watermarking is becoming increasingly important with the advent of Large Language Models (LLM). LLMs can generate texts that cannot be distinguished from human-written texts. This is a serious problem for the credibility of the text. Easymark is a simple yet effective solution to this problem. Easymark can inject a watermark without changing the meaning of the text at all while a validator can detect if a text was generated from a system that adopted Easymark or not with high credibility. Easymark is extremely easy to implement so that it only requires a few lines of code. Easymark does not require access to LLMs, so it can be implemented on the user-side when the LLM providers do not offer watermarked LLMs. In spite of its simplicity, it achieves higher detection accuracy and BLEU scores than the state-of-the-art text watermarking methods. We also prove the impossibility theorem of perfect watermarking, which is valuable in its own right. This theorem shows that no matter how sophisticated a watermark is, a malicious user could remove it from the text, which motivate us to use a simple watermark such as Easymark. We carry out experiments with LLM-generated texts and confirm that Easymark can be detected reliably without any degradation of BLEU and perplexity, and outperform state-of-the-art watermarks in terms of both quality and reliability.
Necessary and Sufficient Watermark for Large Language Models
Oct 02, 2023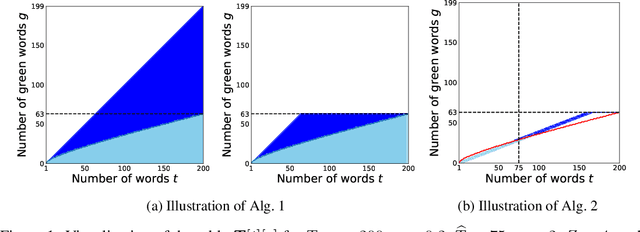


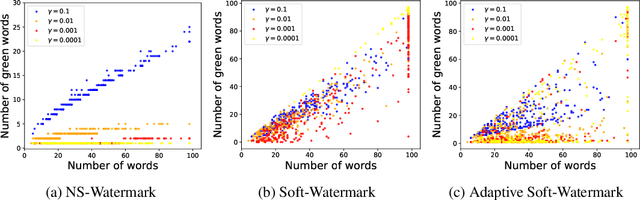
Abstract:In recent years, large language models (LLMs) have achieved remarkable performances in various NLP tasks. They can generate texts that are indistinguishable from those written by humans. Such remarkable performance of LLMs increases their risk of being used for malicious purposes, such as generating fake news articles. Therefore, it is necessary to develop methods for distinguishing texts written by LLMs from those written by humans. Watermarking is one of the most powerful methods for achieving this. Although existing watermarking methods have successfully detected texts generated by LLMs, they significantly degrade the quality of the generated texts. In this study, we propose the Necessary and Sufficient Watermark (NS-Watermark) for inserting watermarks into generated texts without degrading the text quality. More specifically, we derive minimum constraints required to be imposed on the generated texts to distinguish whether LLMs or humans write the texts. Then, we formulate the NS-Watermark as a constrained optimization problem and propose an efficient algorithm to solve it. Through the experiments, we demonstrate that the NS-Watermark can generate more natural texts than existing watermarking methods and distinguish more accurately between texts written by LLMs and those written by humans. Especially in machine translation tasks, the NS-Watermark can outperform the existing watermarking method by up to 30 BLEU scores.
Beyond Exponential Graph: Communication-Efficient Topologies for Decentralized Learning via Finite-time Convergence
May 19, 2023Abstract:Decentralized learning has recently been attracting increasing attention for its applications in parallel computation and privacy preservation. Many recent studies stated that the underlying network topology with a faster consensus rate (a.k.a. spectral gap) leads to a better convergence rate and accuracy for decentralized learning. However, a topology with a fast consensus rate, e.g., the exponential graph, generally has a large maximum degree, which incurs significant communication costs. Thus, seeking topologies with both a fast consensus rate and small maximum degree is important. In this study, we propose a novel topology combining both a fast consensus rate and small maximum degree called the Base-$(k + 1)$ Graph. Unlike the existing topologies, the Base-$(k + 1)$ Graph enables all nodes to reach the exact consensus after a finite number of iterations for any number of nodes and maximum degree k. Thanks to this favorable property, the Base-$(k + 1)$ Graph endows Decentralized SGD (DSGD) with both a faster convergence rate and more communication efficiency than the exponential graph. We conducted experiments with various topologies, demonstrating that the Base-$(k + 1)$ Graph enables various decentralized learning methods to achieve higher accuracy with better communication efficiency than the existing topologies.
Momentum Tracking: Momentum Acceleration for Decentralized Deep Learning on Heterogeneous Data
Sep 30, 2022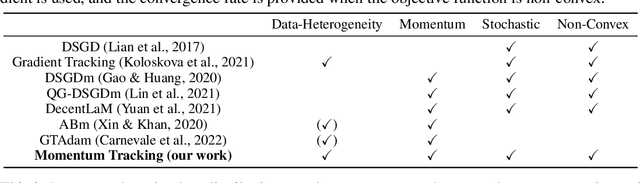
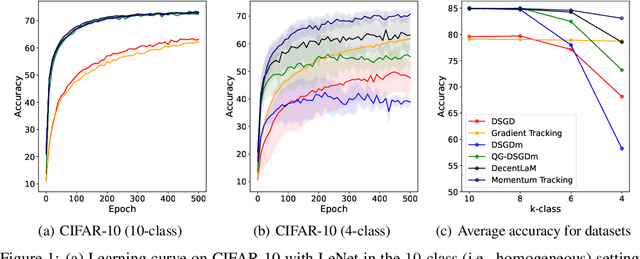
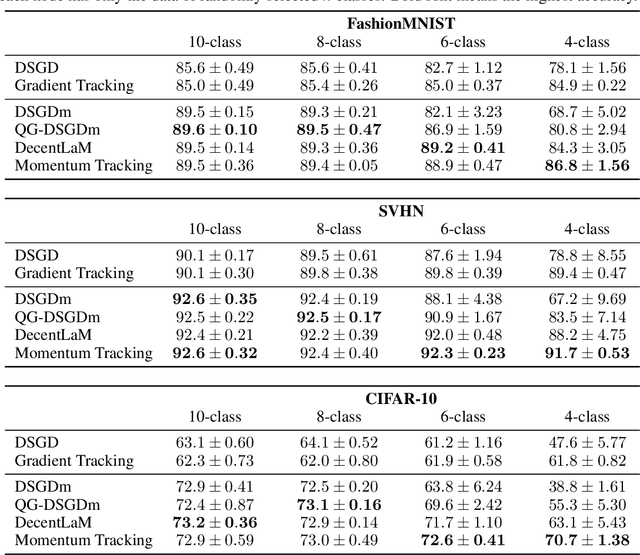
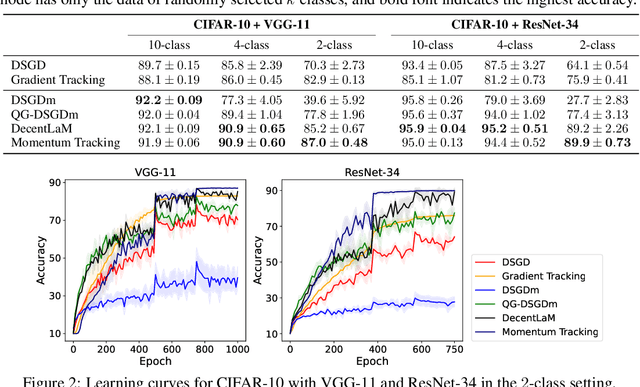
Abstract:SGD with momentum acceleration is one of the key components for improving the performance of neural networks. For decentralized learning, a straightforward approach using momentum acceleration is Distributed SGD (DSGD) with momentum acceleration (DSGDm). However, DSGDm performs worse than DSGD when the data distributions are statistically heterogeneous. Recently, several studies have addressed this issue and proposed methods with momentum acceleration that are more robust to data heterogeneity than DSGDm, although their convergence rates remain dependent on data heterogeneity and decrease when the data distributions are heterogeneous. In this study, we propose Momentum Tracking, which is a method with momentum acceleration whose convergence rate is proven to be independent of data heterogeneity. More specifically, we analyze the convergence rate of Momentum Tracking in the standard deep learning setting, where the objective function is non-convex and the stochastic gradient is used. Then, we identify that it is independent of data heterogeneity for any momentum coefficient $\beta\in [0, 1)$. Through image classification tasks, we demonstrate that Momentum Tracking is more robust to data heterogeneity than the existing decentralized learning methods with momentum acceleration and can consistently outperform these existing methods when the data distributions are heterogeneous.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge