Deborah Sulem
An Empirical Study of Simplicial Representation Learning with Wasserstein Distance
Oct 16, 2023Abstract:In this paper, we delve into the problem of simplicial representation learning utilizing the 1-Wasserstein distance on a tree structure (a.k.a., Tree-Wasserstein distance (TWD)), where TWD is defined as the L1 distance between two tree-embedded vectors. Specifically, we consider a framework for simplicial representation estimation employing a self-supervised learning approach based on SimCLR with a negative TWD as a similarity measure. In SimCLR, the cosine similarity with real-vector embeddings is often utilized; however, it has not been well studied utilizing L1-based measures with simplicial embeddings. A key challenge is that training the L1 distance is numerically challenging and often yields unsatisfactory outcomes, and there are numerous choices for probability models. Thus, this study empirically investigates a strategy for optimizing self-supervised learning with TWD and find a stable training procedure. More specifically, we evaluate the combination of two types of TWD (total variation and ClusterTree) and several simplicial models including the softmax function, the ArcFace probability model, and simplicial embedding. Moreover, we propose a simple yet effective Jeffrey divergence-based regularization method to stabilize the optimization. Through empirical experiments on STL10, CIFAR10, CIFAR100, and SVHN, we first found that the simple combination of softmax function and TWD can obtain significantly lower results than the standard SimCLR (non-simplicial model and cosine similarity). We found that the model performance depends on the combination of TWD and the simplicial model, and the Jeffrey divergence regularization usually helps model training. Finally, we inferred that the appropriate choice of combination of TWD and simplicial models outperformed cosine similarity based representation learning.
Scalable Variational Bayes methods for Hawkes processes
Dec 01, 2022



Abstract:Multivariate Hawkes processes are temporal point processes extensively applied to model event data with dependence on past occurrences and interaction phenomena. In the generalised nonlinear model, positive and negative interactions between the components of the process are allowed, therefore accounting for so-called excitation and inhibition effects. In the nonparametric setting, learning the temporal dependence structure of Hawkes processes is often a computationally expensive task, all the more with Bayesian estimation methods. In general, the posterior distribution in the nonlinear Hawkes model is non-conjugate and doubly intractable. Moreover, existing Monte-Carlo Markov Chain methods are often slow and not scalable to high-dimensional processes in practice. Recently, efficient algorithms targeting a mean-field variational approximation of the posterior distribution have been proposed. In this work, we unify existing variational Bayes inference approaches under a general framework, that we theoretically analyse under easily verifiable conditions on the prior, the variational class, and the model. We notably apply our theory to a novel spike-and-slab variational class, that can induce sparsity through the connectivity graph parameter of the multivariate Hawkes model. Then, in the context of the popular sigmoid Hawkes model, we leverage existing data augmentation technique and design adaptive and sparsity-inducing mean-field variational methods. In particular, we propose a two-step algorithm based on a thresholding heuristic to select the graph parameter. Through an extensive set of numerical simulations, we demonstrate that our approach enjoys several benefits: it is computationally efficient, can reduce the dimensionality of the problem by selecting the graph parameter, and is able to adapt to the smoothness of the underlying parameter.
Graph similarity learning for change-point detection in dynamic networks
Mar 29, 2022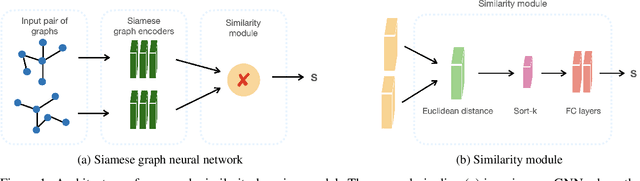
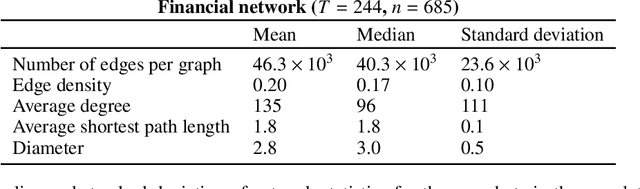
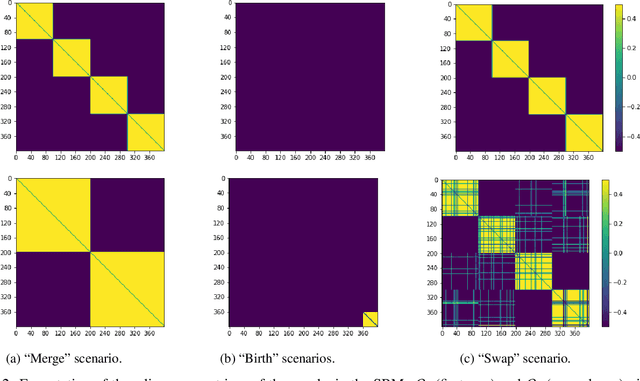
Abstract:Dynamic networks are ubiquitous for modelling sequential graph-structured data, e.g., brain connectome, population flows and messages exchanges. In this work, we consider dynamic networks that are temporal sequences of graph snapshots, and aim at detecting abrupt changes in their structure. This task is often termed network change-point detection and has numerous applications, such as fraud detection or physical motion monitoring. Leveraging a graph neural network model, we design a method to perform online network change-point detection that can adapt to the specific network domain and localise changes with no delay. The main novelty of our method is to use a siamese graph neural network architecture for learning a data-driven graph similarity function, which allows to effectively compare the current graph and its recent history. Importantly, our method does not require prior knowledge on the network generative distribution and is agnostic to the type of change-points; moreover, it can be applied to a large variety of networks, that include for instance edge weights and node attributes. We show on synthetic and real data that our method enjoys a number of benefits: it is able to learn an adequate graph similarity function for performing online network change-point detection in diverse types of change-point settings, and requires a shorter data history to detect changes than most existing state-of-the-art baselines.
Diverse Counterfactual Explanations for Anomaly Detection in Time Series
Mar 21, 2022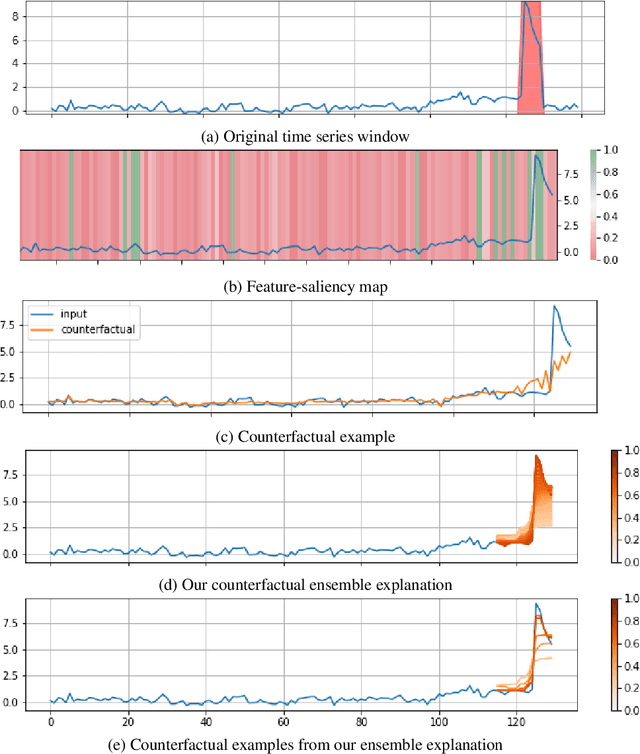

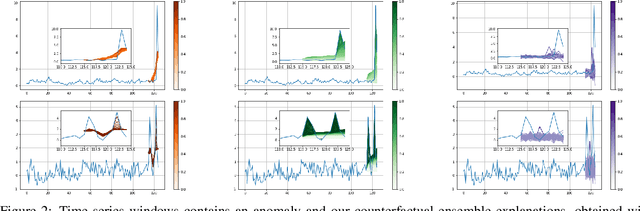
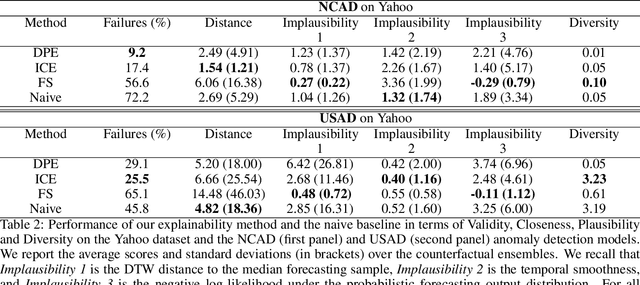
Abstract:Data-driven methods that detect anomalies in times series data are ubiquitous in practice, but they are in general unable to provide helpful explanations for the predictions they make. In this work we propose a model-agnostic algorithm that generates counterfactual ensemble explanations for time series anomaly detection models. Our method generates a set of diverse counterfactual examples, i.e, multiple perturbed versions of the original time series that are not considered anomalous by the detection model. Since the magnitude of the perturbations is limited, these counterfactuals represent an ensemble of inputs similar to the original time series that the model would deem normal. Our algorithm is applicable to any differentiable anomaly detection model. We investigate the value of our method on univariate and multivariate real-world datasets and two deep-learning-based anomaly detection models, under several explainability criteria previously proposed in other data domains such as Validity, Plausibility, Closeness and Diversity. We show that our algorithm can produce ensembles of counterfactual examples that satisfy these criteria and thanks to a novel type of visualisation, can convey a richer interpretation of a model's internal mechanism than existing methods. Moreover, we design a sparse variant of our method to improve the interpretability of counterfactual explanations for high-dimensional time series anomalies. In this setting, our explanation is localised on only a few dimensions and can therefore be communicated more efficiently to the model's user.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge