Deep Non-Parametric Time Series Forecaster

This paper presents non-parametric baseline models for time series forecasting. Unlike classical forecasting models, the proposed approach does not assume any parametric form for the predictive distribution and instead generates predictions by sampling from the empirical distribution according to a tunable strategy. By virtue of this, the model is always able to produce reasonable forecasts (i.e., predictions within the observed data range) without fail unlike classical models that suffer from numerical stability on some data distributions. Moreover, we develop a global version of the proposed method that automatically learns the sampling strategy by exploiting the information across multiple related time series. The empirical evaluation shows that the proposed methods have reasonable and consistent performance across all datasets, proving them to be strong baselines to be considered in one's forecasting toolbox.

Criteria for Classifying Forecasting Methods

Classifying forecasting methods as being either of a "machine learning" or "statistical" nature has become commonplace in parts of the forecasting literature and community, as exemplified by the M4 competition and the conclusion drawn by the organizers. We argue that this distinction does not stem from fundamental differences in the methods assigned to either class. Instead, this distinction is probably of a tribal nature, which limits the insights into the appropriateness and effectiveness of different forecasting methods. We provide alternative characteristics of forecasting methods which, in our view, allow to draw meaningful conclusions. Further, we discuss areas of forecasting which could benefit most from cross-pollination between the ML and the statistics communities.

On the detrimental effect of invariances in the likelihood for variational inference

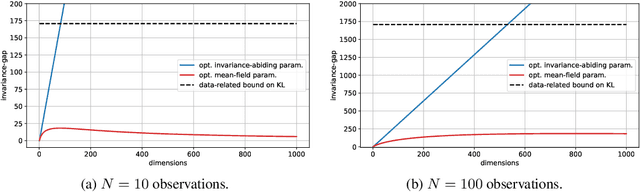
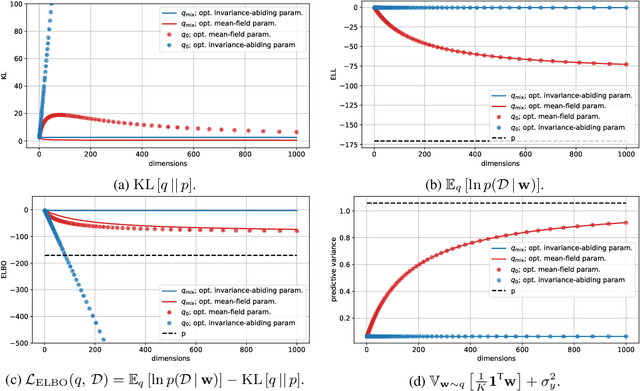
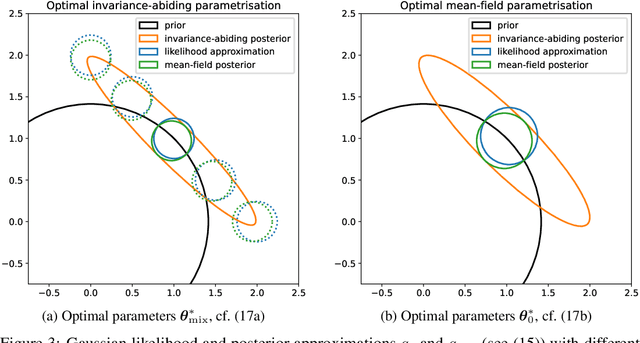
Variational Bayesian posterior inference often requires simplifying approximations such as mean-field parametrisation to ensure tractability. However, prior work has associated the variational mean-field approximation for Bayesian neural networks with underfitting in the case of small datasets or large model sizes. In this work, we show that invariances in the likelihood function of over-parametrised models contribute to this phenomenon because these invariances complicate the structure of the posterior by introducing discrete and/or continuous modes which cannot be well approximated by Gaussian mean-field distributions. In particular, we show that the mean-field approximation has an additional gap in the evidence lower bound compared to a purpose-built posterior that takes into account the known invariances. Importantly, this invariance gap is not constant; it vanishes as the approximation reverts to the prior. We proceed by first considering translation invariances in a linear model with a single data point in detail. We show that, while the true posterior can be constructed from a mean-field parametrisation, this is achieved only if the objective function takes into account the invariance gap. Then, we transfer our analysis of the linear model to neural networks. Our analysis provides a framework for future work to explore solutions to the invariance problem.

Intrinsic Anomaly Detection for Multi-Variate Time Series

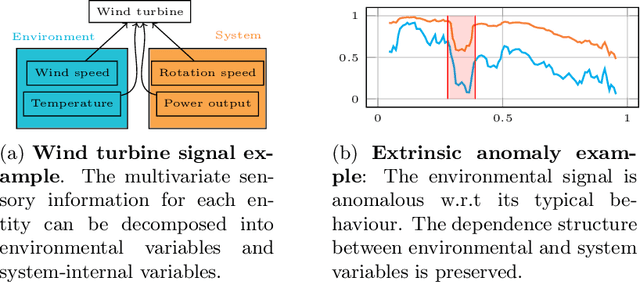
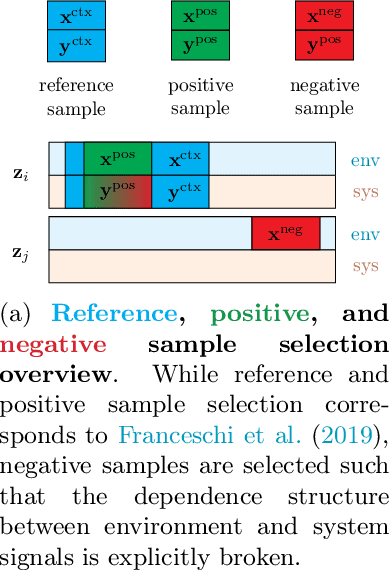
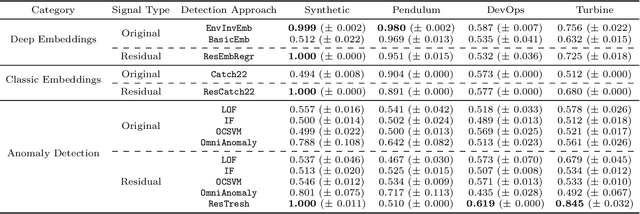
We introduce a novel, practically relevant variation of the anomaly detection problem in multi-variate time series: intrinsic anomaly detection. It appears in diverse practical scenarios ranging from DevOps to IoT, where we want to recognize failures of a system that operates under the influence of a surrounding environment. Intrinsic anomalies are changes in the functional dependency structure between time series that represent an environment and time series that represent the internal state of a system that is placed in said environment. We formalize this problem, provide under-studied public and new purpose-built data sets for it, and present methods that handle intrinsic anomaly detection. These address the short-coming of existing anomaly detection methods that cannot differentiate between expected changes in the system's state and unexpected ones, i.e., changes in the system that deviate from the environment's influence. Our most promising approach is fully unsupervised and combines adversarial learning and time series representation learning, thereby addressing problems such as label sparsity and subjectivity, while allowing to navigate and improve notoriously problematic anomaly detection data sets.

Diverse Counterfactual Explanations for Anomaly Detection in Time Series

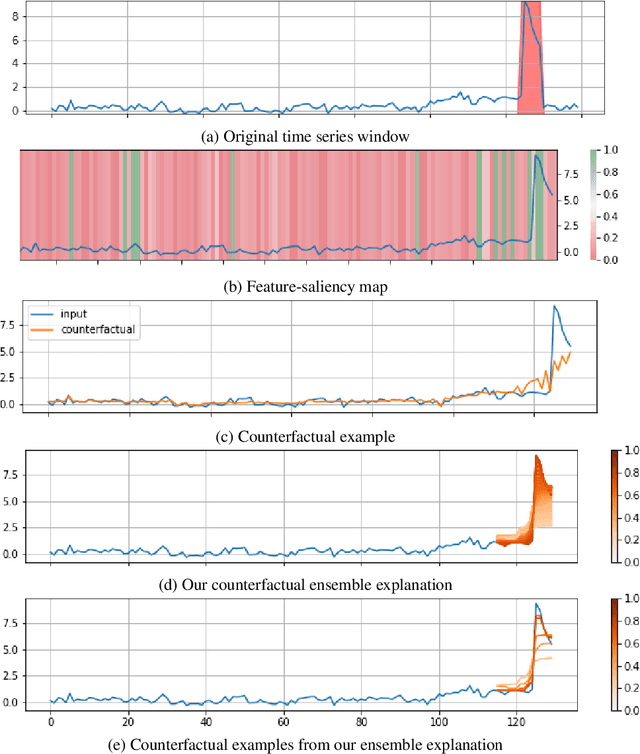
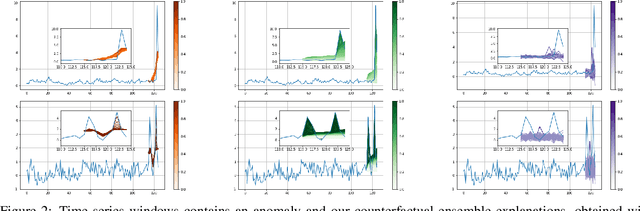
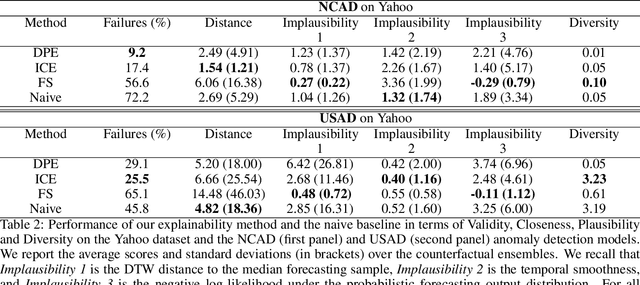
Data-driven methods that detect anomalies in times series data are ubiquitous in practice, but they are in general unable to provide helpful explanations for the predictions they make. In this work we propose a model-agnostic algorithm that generates counterfactual ensemble explanations for time series anomaly detection models. Our method generates a set of diverse counterfactual examples, i.e, multiple perturbed versions of the original time series that are not considered anomalous by the detection model. Since the magnitude of the perturbations is limited, these counterfactuals represent an ensemble of inputs similar to the original time series that the model would deem normal. Our algorithm is applicable to any differentiable anomaly detection model. We investigate the value of our method on univariate and multivariate real-world datasets and two deep-learning-based anomaly detection models, under several explainability criteria previously proposed in other data domains such as Validity, Plausibility, Closeness and Diversity. We show that our algorithm can produce ensembles of counterfactual examples that satisfy these criteria and thanks to a novel type of visualisation, can convey a richer interpretation of a model's internal mechanism than existing methods. Moreover, we design a sparse variant of our method to improve the interpretability of counterfactual explanations for high-dimensional time series anomalies. In this setting, our explanation is localised on only a few dimensions and can therefore be communicated more efficiently to the model's user.

Multivariate Quantile Function Forecaster

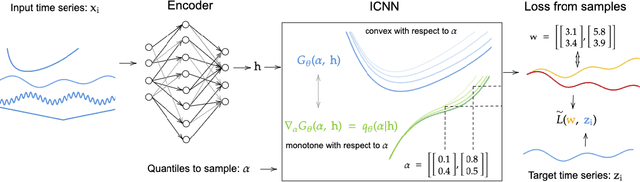
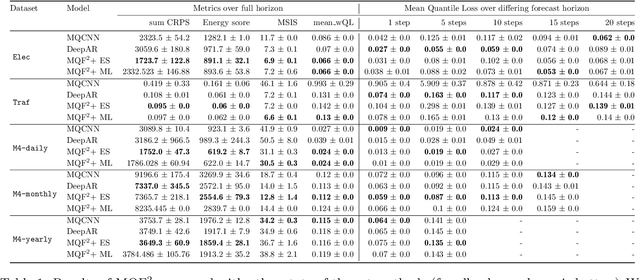
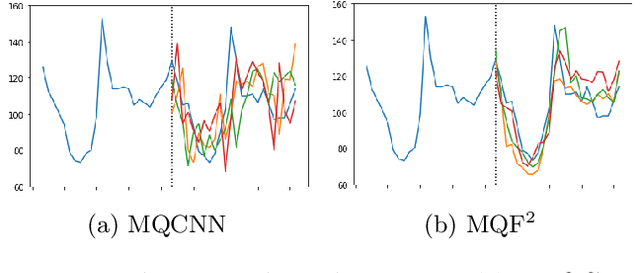
We propose Multivariate Quantile Function Forecaster (MQF$^2$), a global probabilistic forecasting method constructed using a multivariate quantile function and investigate its application to multi-horizon forecasting. Prior approaches are either autoregressive, implicitly capturing the dependency structure across time but exhibiting error accumulation with increasing forecast horizons, or multi-horizon sequence-to-sequence models, which do not exhibit error accumulation, but also do typically not model the dependency structure across time steps. MQF$^2$ combines the benefits of both approaches, by directly making predictions in the form of a multivariate quantile function, defined as the gradient of a convex function which we parametrize using input-convex neural networks. By design, the quantile function is monotone with respect to the input quantile levels and hence avoids quantile crossing. We provide two options to train MQF$^2$: with energy score or with maximum likelihood. Experimental results on real-world and synthetic datasets show that our model has comparable performance with state-of-the-art methods in terms of single time step metrics while capturing the time dependency structure.

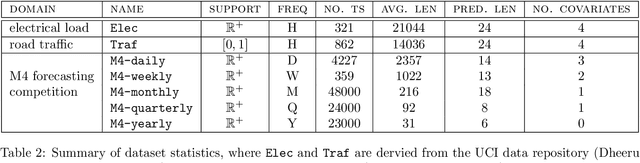
Online Time Series Anomaly Detection with State Space Gaussian Processes

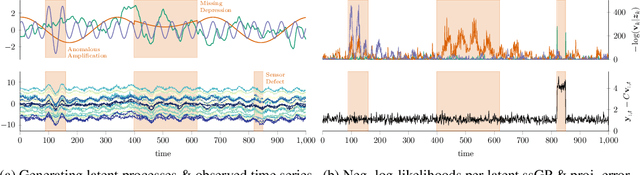
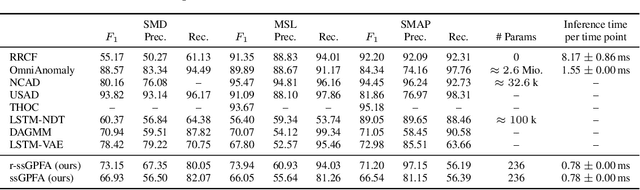
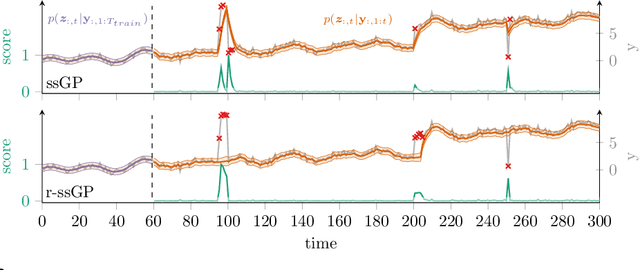
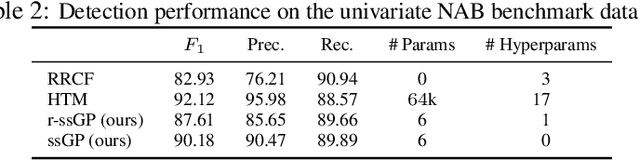
We propose r-ssGPFA, an unsupervised online anomaly detection model for uni- and multivariate time series building on the efficient state space formulation of Gaussian processes. For high-dimensional time series, we propose an extension of Gaussian process factor analysis to identify the common latent processes of the time series, allowing us to detect anomalies efficiently in an interpretable manner. We gain explainability while speeding up computations by imposing an orthogonality constraint on the mapping from the latent to the observed. Our model's robustness is improved by using a simple heuristic to skip Kalman updates when encountering anomalous observations. We investigate the behaviour of our model on synthetic data and show on standard benchmark datasets that our method is competitive with state-of-the-art methods while being computationally cheaper.

Monte Carlo EM for Deep Time Series Anomaly Detection

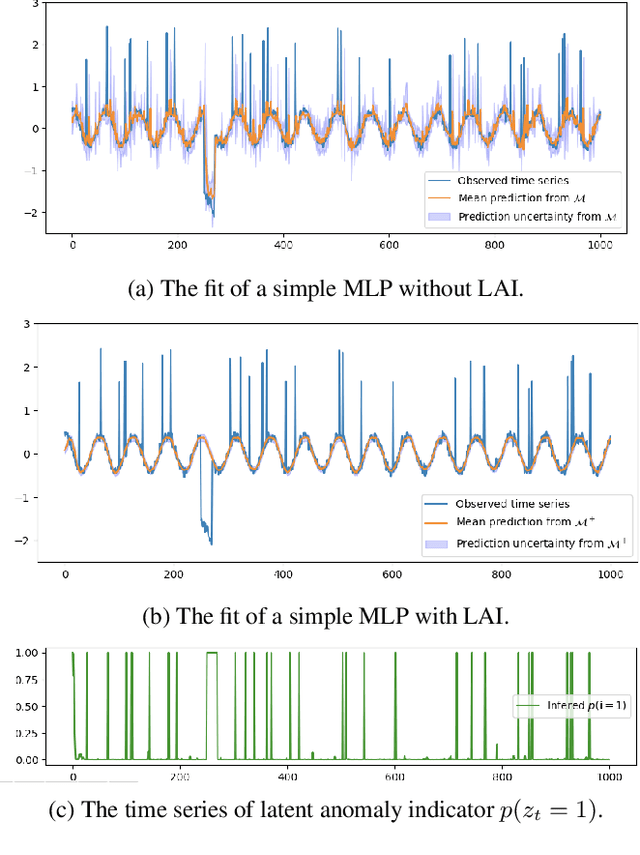
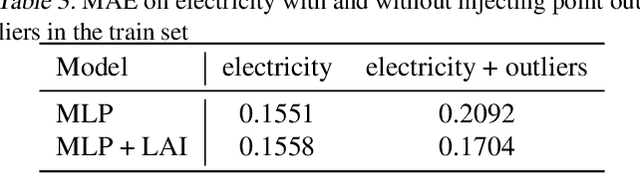
Time series data are often corrupted by outliers or other kinds of anomalies. Identifying the anomalous points can be a goal on its own (anomaly detection), or a means to improving performance of other time series tasks (e.g. forecasting). Recent deep-learning-based approaches to anomaly detection and forecasting commonly assume that the proportion of anomalies in the training data is small enough to ignore, and treat the unlabeled data as coming from the nominal data distribution. We present a simple yet effective technique for augmenting existing time series models so that they explicitly account for anomalies in the training data. By augmenting the training data with a latent anomaly indicator variable whose distribution is inferred while training the underlying model using Monte Carlo EM, our method simultaneously infers anomalous points while improving model performance on nominal data. We demonstrate the effectiveness of the approach by combining it with a simple feed-forward forecasting model. We investigate how anomalies in the train set affect the training of forecasting models, which are commonly used for time series anomaly detection, and show that our method improves the training of the model.

Learning Quantile Functions without Quantile Crossing for Distribution-free Time Series Forecasting

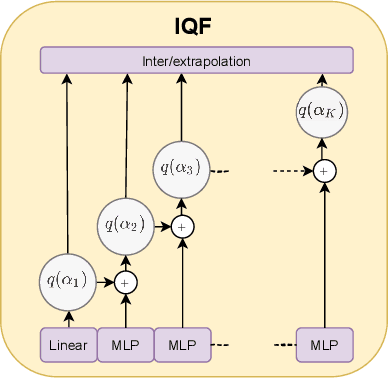
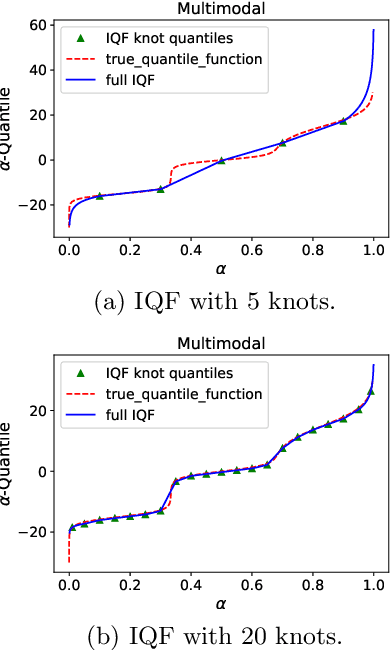
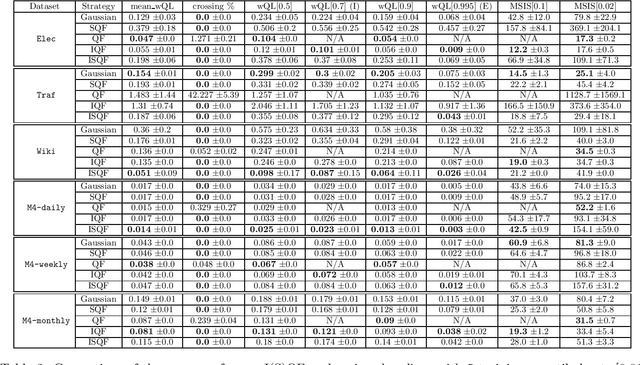
Quantile regression is an effective technique to quantify uncertainty, fit challenging underlying distributions, and often provide full probabilistic predictions through joint learnings over multiple quantile levels. A common drawback of these joint quantile regressions, however, is \textit{quantile crossing}, which violates the desirable monotone property of the conditional quantile function. In this work, we propose the Incremental (Spline) Quantile Functions I(S)QF, a flexible and efficient distribution-free quantile estimation framework that resolves quantile crossing with a simple neural network layer. Moreover, I(S)QF inter/extrapolate to predict arbitrary quantile levels that differ from the underlying training ones. Equipped with the analytical evaluation of the continuous ranked probability score of I(S)QF representations, we apply our methods to NN-based times series forecasting cases, where the savings of the expensive re-training costs for non-trained quantile levels is particularly significant. We also provide a generalization error analysis of our proposed approaches under the sequence-to-sequence setting. Lastly, extensive experiments demonstrate the improvement of consistency and accuracy errors over other baselines.

A Study of Joint Graph Inference and Forecasting

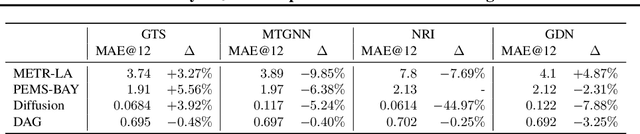
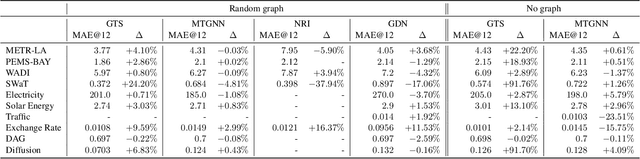
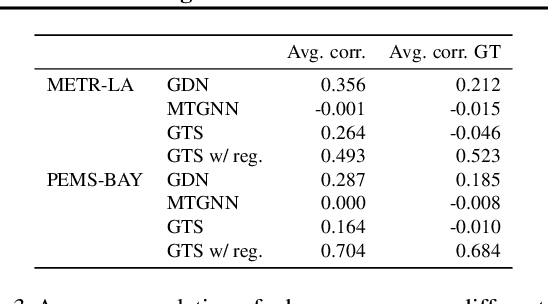
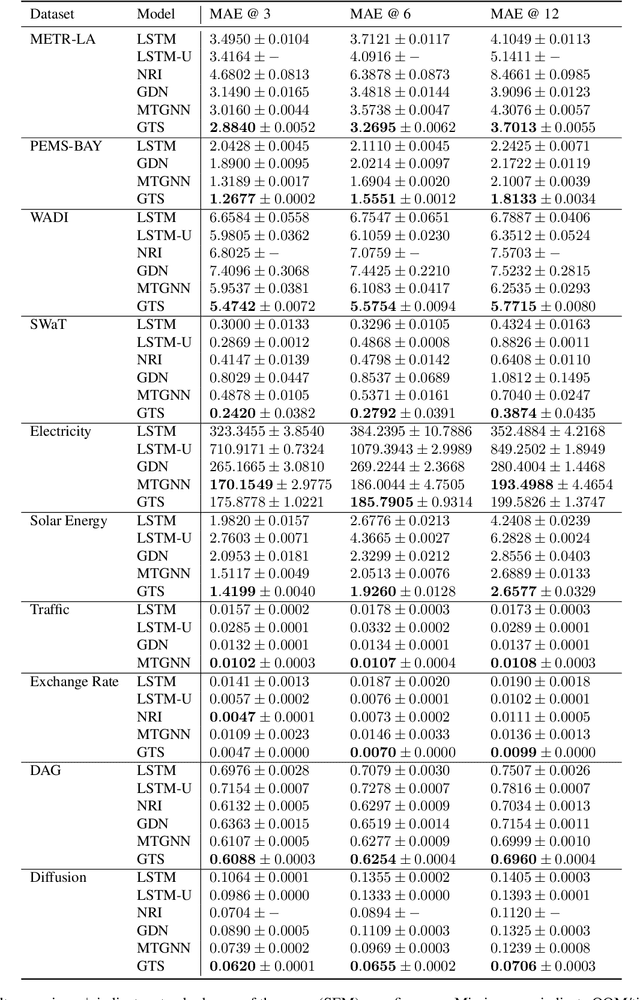
We study a recent class of models which uses graph neural networks (GNNs) to improve forecasting in multivariate time series. The core assumption behind these models is that there is a latent graph between the time series (nodes) that governs the evolution of the multivariate time series. By parameterizing a graph in a differentiable way, the models aim to improve forecasting quality. We compare four recent models of this class on the forecasting task. Further, we perform ablations to study their behavior under changing conditions, e.g., when disabling the graph-learning modules and providing the ground-truth relations instead. Based on our findings, we propose novel ways of combining the existing architectures.