Solving Recurrent MIPs with Semi-supervised Graph Neural Networks

We propose an ML-based model that automates and expedites the solution of MIPs by predicting the values of variables. Our approach is motivated by the observation that many problem instances share salient features and solution structures since they differ only in few (time-varying) parameters. Examples include transportation and routing problems where decisions need to be re-optimized whenever commodity volumes or link costs change. Our method is the first to exploit the sequential nature of the instances being solved periodically, and can be trained with ``unlabeled'' instances, when exact solutions are unavailable, in a semi-supervised setting. Also, we provide a principled way of transforming the probabilistic predictions into integral solutions. Using a battery of experiments with representative binary MIPs, we show the gains of our model over other ML-based optimization approaches.

Multivariate Quantile Function Forecaster

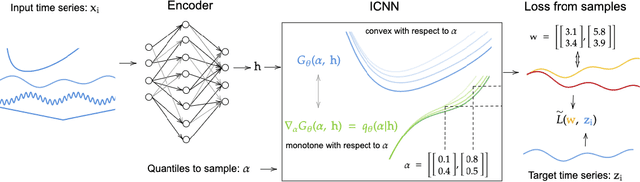
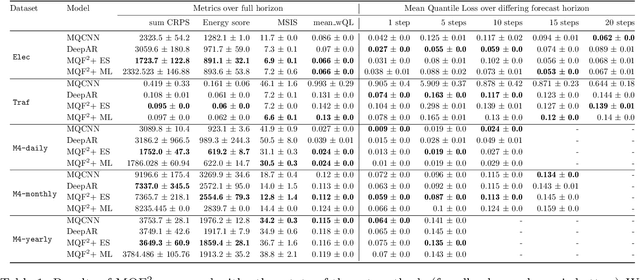
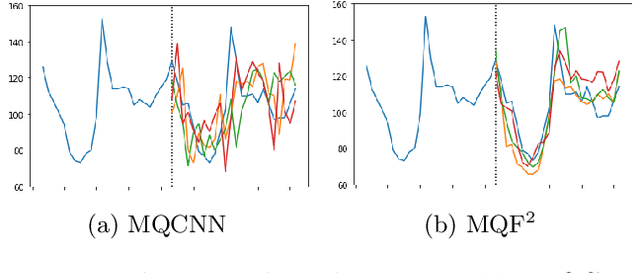
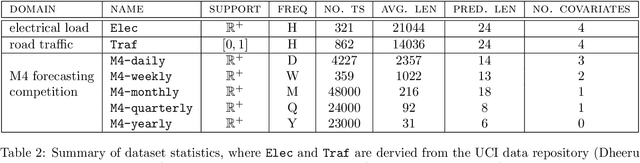
We propose Multivariate Quantile Function Forecaster (MQF$^2$), a global probabilistic forecasting method constructed using a multivariate quantile function and investigate its application to multi-horizon forecasting. Prior approaches are either autoregressive, implicitly capturing the dependency structure across time but exhibiting error accumulation with increasing forecast horizons, or multi-horizon sequence-to-sequence models, which do not exhibit error accumulation, but also do typically not model the dependency structure across time steps. MQF$^2$ combines the benefits of both approaches, by directly making predictions in the form of a multivariate quantile function, defined as the gradient of a convex function which we parametrize using input-convex neural networks. By design, the quantile function is monotone with respect to the input quantile levels and hence avoids quantile crossing. We provide two options to train MQF$^2$: with energy score or with maximum likelihood. Experimental results on real-world and synthetic datasets show that our model has comparable performance with state-of-the-art methods in terms of single time step metrics while capturing the time dependency structure.

Deep Explicit Duration Switching Models for Time Series

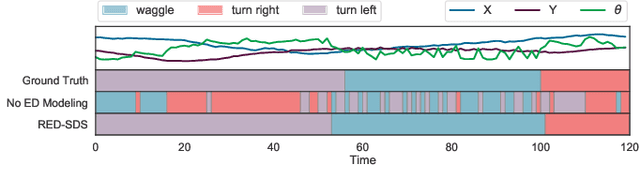
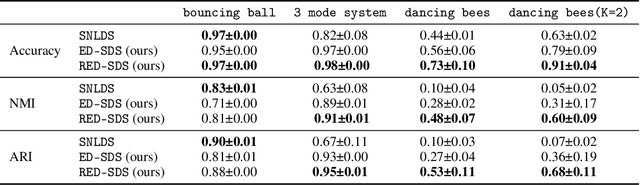
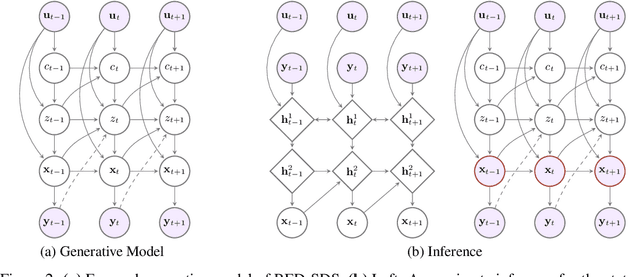
Many complex time series can be effectively subdivided into distinct regimes that exhibit persistent dynamics. Discovering the switching behavior and the statistical patterns in these regimes is important for understanding the underlying dynamical system. We propose the Recurrent Explicit Duration Switching Dynamical System (RED-SDS), a flexible model that is capable of identifying both state- and time-dependent switching dynamics. State-dependent switching is enabled by a recurrent state-to-switch connection and an explicit duration count variable is used to improve the time-dependent switching behavior. We demonstrate how to perform efficient inference using a hybrid algorithm that approximates the posterior of the continuous states via an inference network and performs exact inference for the discrete switches and counts. The model is trained by maximizing a Monte Carlo lower bound of the marginal log-likelihood that can be computed efficiently as a byproduct of the inference routine. Empirical results on multiple datasets demonstrate that RED-SDS achieves considerable improvement in time series segmentation and competitive forecasting performance against the state of the art.

Neural forecasting: Introduction and literature overview

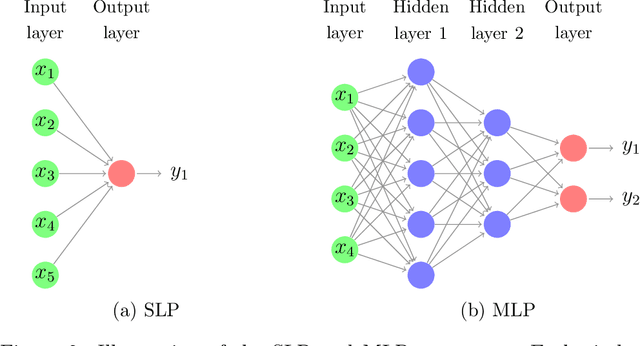
Neural network based forecasting methods have become ubiquitous in large-scale industrial forecasting applications over the last years. As the prevalence of neural network based solutions among the best entries in the recent M4 competition shows, the recent popularity of neural forecasting methods is not limited to industry and has also reached academia. This article aims at providing an introduction and an overview of some of the advances that have permitted the resurgence of neural networks in machine learning. Building on these foundations, the article then gives an overview of the recent literature on neural networks for forecasting and applications.

GluonTS: Probabilistic Time Series Models in Python

We introduce Gluon Time Series (GluonTS, available at https://gluon-ts.mxnet.io), a library for deep-learning-based time series modeling. GluonTS simplifies the development of and experimentation with time series models for common tasks such as forecasting or anomaly detection. It provides all necessary components and tools that scientists need for quickly building new models, for efficiently running and analyzing experiments and for evaluating model accuracy.

Orthogonal Sparse PCA and Covariance Estimation via Procrustes Reformulation

The problem of estimating sparse eigenvectors of a symmetric matrix attracts a lot of attention in many applications, especially those with high dimensional data set. While classical eigenvectors can be obtained as the solution of a maximization problem, existing approaches formulate this problem by adding a penalty term into the objective function that encourages a sparse solution. However, the resulting methods achieve sparsity at the expense of sacrificing the orthogonality property. In this paper, we develop a new method to estimate dominant sparse eigenvectors without trading off their orthogonality. The problem is highly non-convex and hard to handle. We apply the MM framework where we iteratively maximize a tight lower bound (surrogate function) of the objective function over the Stiefel manifold. The inner maximization problem turns out to be a rectangular Procrustes problem, which has a closed form solution. In addition, we propose a method to improve the covariance estimation problem when its underlying eigenvectors are known to be sparse. We use the eigenvalue decomposition of the covariance matrix to formulate an optimization problem where we impose sparsity on the corresponding eigenvectors. Numerical experiments show that the proposed eigenvector extraction algorithm matches or outperforms existing algorithms in terms of support recovery and explained variance, while the covariance estimation algorithms improve significantly the sample covariance estimator.