Obeying the Order: Introducing Ordered Transfer Hyperparameter Optimisation

We introduce ordered transfer hyperparameter optimisation (OTHPO), a version of transfer learning for hyperparameter optimisation (HPO) where the tasks follow a sequential order. Unlike for state-of-the-art transfer HPO, the assumption is that each task is most correlated to those immediately before it. This matches many deployed settings, where hyperparameters are retuned as more data is collected; for instance tuning a sequence of movie recommendation systems as more movies and ratings are added. We propose a formal definition, outline the differences to related problems and propose a basic OTHPO method that outperforms state-of-the-art transfer HPO. We empirically show the importance of taking order into account using ten benchmarks. The benchmarks are in the setting of gradually accumulating data, and span XGBoost, random forest, approximate k-nearest neighbor, elastic net, support vector machines and a separate real-world motivated optimisation problem. We open source the benchmarks to foster future research on ordered transfer HPO.

Multivariate Quantile Function Forecaster

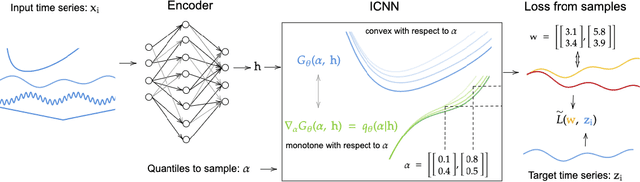
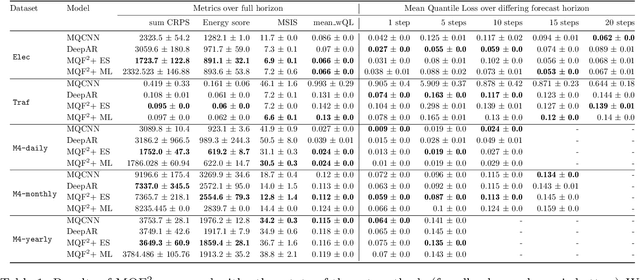
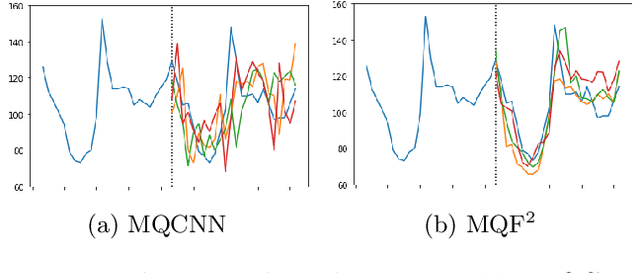
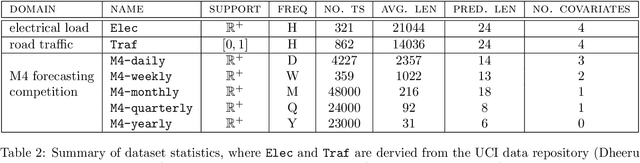
We propose Multivariate Quantile Function Forecaster (MQF$^2$), a global probabilistic forecasting method constructed using a multivariate quantile function and investigate its application to multi-horizon forecasting. Prior approaches are either autoregressive, implicitly capturing the dependency structure across time but exhibiting error accumulation with increasing forecast horizons, or multi-horizon sequence-to-sequence models, which do not exhibit error accumulation, but also do typically not model the dependency structure across time steps. MQF$^2$ combines the benefits of both approaches, by directly making predictions in the form of a multivariate quantile function, defined as the gradient of a convex function which we parametrize using input-convex neural networks. By design, the quantile function is monotone with respect to the input quantile levels and hence avoids quantile crossing. We provide two options to train MQF$^2$: with energy score or with maximum likelihood. Experimental results on real-world and synthetic datasets show that our model has comparable performance with state-of-the-art methods in terms of single time step metrics while capturing the time dependency structure.

Online Time Series Anomaly Detection with State Space Gaussian Processes

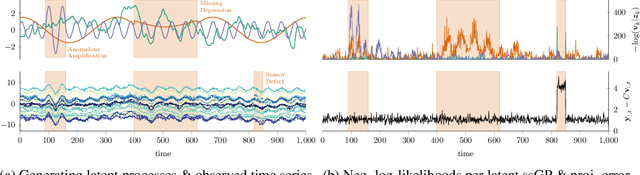
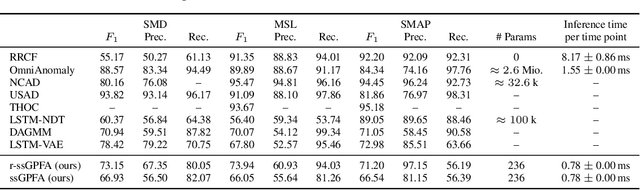
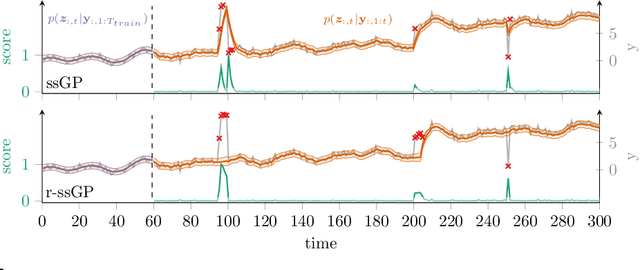
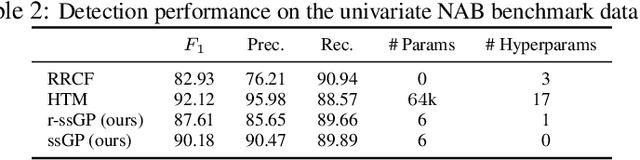
We propose r-ssGPFA, an unsupervised online anomaly detection model for uni- and multivariate time series building on the efficient state space formulation of Gaussian processes. For high-dimensional time series, we propose an extension of Gaussian process factor analysis to identify the common latent processes of the time series, allowing us to detect anomalies efficiently in an interpretable manner. We gain explainability while speeding up computations by imposing an orthogonality constraint on the mapping from the latent to the observed. Our model's robustness is improved by using a simple heuristic to skip Kalman updates when encountering anomalous observations. We investigate the behaviour of our model on synthetic data and show on standard benchmark datasets that our method is competitive with state-of-the-art methods while being computationally cheaper.

Monte Carlo EM for Deep Time Series Anomaly Detection

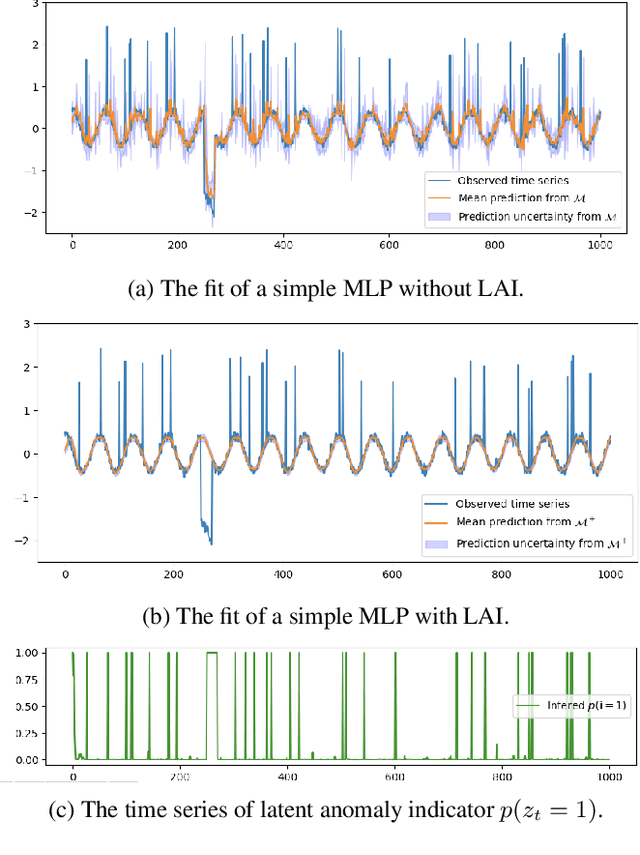
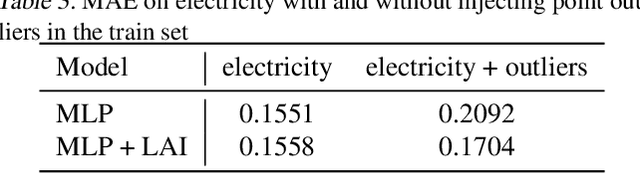
Time series data are often corrupted by outliers or other kinds of anomalies. Identifying the anomalous points can be a goal on its own (anomaly detection), or a means to improving performance of other time series tasks (e.g. forecasting). Recent deep-learning-based approaches to anomaly detection and forecasting commonly assume that the proportion of anomalies in the training data is small enough to ignore, and treat the unlabeled data as coming from the nominal data distribution. We present a simple yet effective technique for augmenting existing time series models so that they explicitly account for anomalies in the training data. By augmenting the training data with a latent anomaly indicator variable whose distribution is inferred while training the underlying model using Monte Carlo EM, our method simultaneously infers anomalous points while improving model performance on nominal data. We demonstrate the effectiveness of the approach by combining it with a simple feed-forward forecasting model. We investigate how anomalies in the train set affect the training of forecasting models, which are commonly used for time series anomaly detection, and show that our method improves the training of the model.

Learning Quantile Functions without Quantile Crossing for Distribution-free Time Series Forecasting

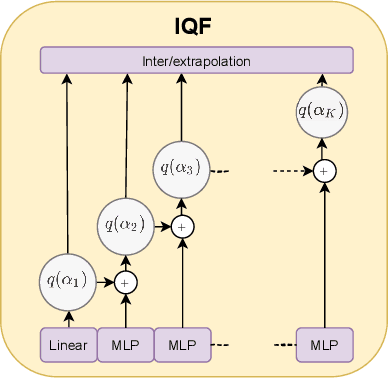
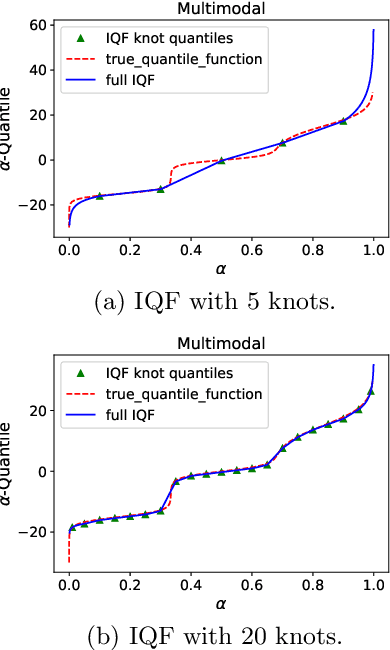
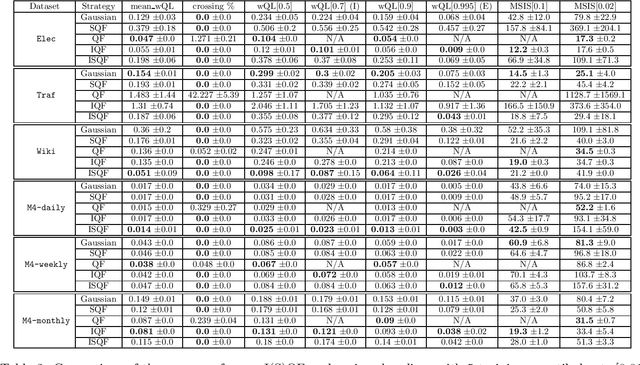
Quantile regression is an effective technique to quantify uncertainty, fit challenging underlying distributions, and often provide full probabilistic predictions through joint learnings over multiple quantile levels. A common drawback of these joint quantile regressions, however, is \textit{quantile crossing}, which violates the desirable monotone property of the conditional quantile function. In this work, we propose the Incremental (Spline) Quantile Functions I(S)QF, a flexible and efficient distribution-free quantile estimation framework that resolves quantile crossing with a simple neural network layer. Moreover, I(S)QF inter/extrapolate to predict arbitrary quantile levels that differ from the underlying training ones. Equipped with the analytical evaluation of the continuous ranked probability score of I(S)QF representations, we apply our methods to NN-based times series forecasting cases, where the savings of the expensive re-training costs for non-trained quantile levels is particularly significant. We also provide a generalization error analysis of our proposed approaches under the sequence-to-sequence setting. Lastly, extensive experiments demonstrate the improvement of consistency and accuracy errors over other baselines.

A Study of Joint Graph Inference and Forecasting

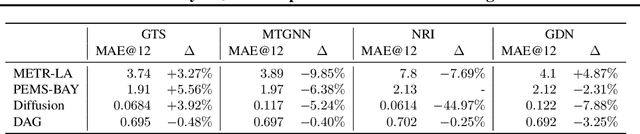
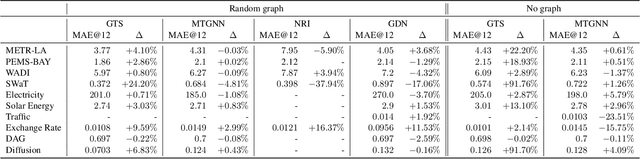
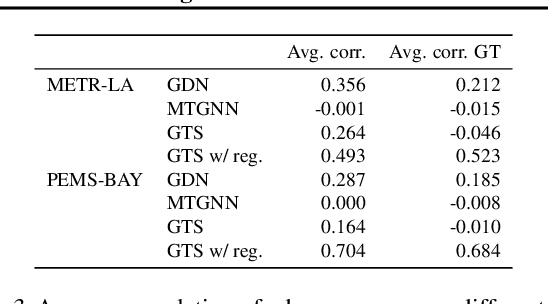
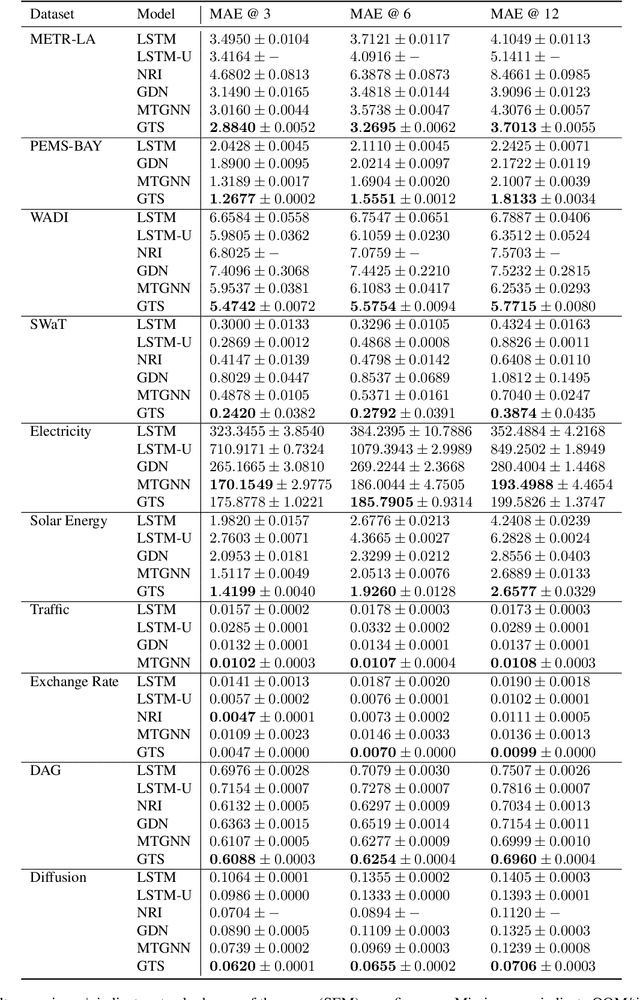
We study a recent class of models which uses graph neural networks (GNNs) to improve forecasting in multivariate time series. The core assumption behind these models is that there is a latent graph between the time series (nodes) that governs the evolution of the multivariate time series. By parameterizing a graph in a differentiable way, the models aim to improve forecasting quality. We compare four recent models of this class on the forecasting task. Further, we perform ablations to study their behavior under changing conditions, e.g., when disabling the graph-learning modules and providing the ground-truth relations instead. Based on our findings, we propose novel ways of combining the existing architectures.

Neural Contextual Anomaly Detection for Time Series

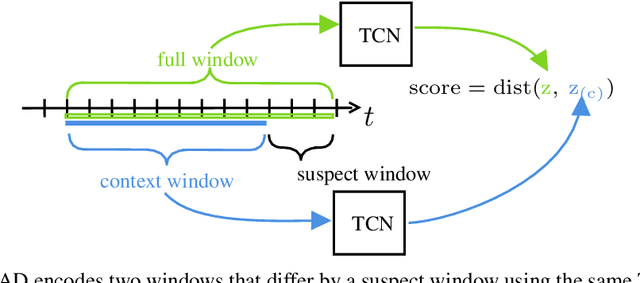
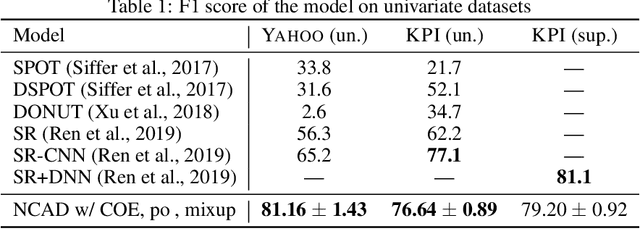
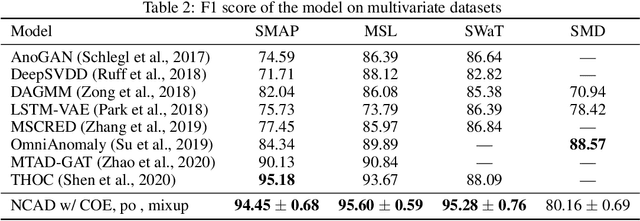
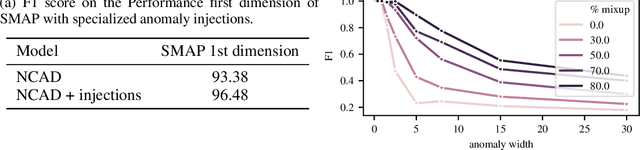
We introduce Neural Contextual Anomaly Detection (NCAD), a framework for anomaly detection on time series that scales seamlessly from the unsupervised to supervised setting, and is applicable to both univariate and multivariate time series. This is achieved by effectively combining recent developments in representation learning for multivariate time series, with techniques for deep anomaly detection originally developed for computer vision that we tailor to the time series setting. Our window-based approach facilitates learning the boundary between normal and anomalous classes by injecting generic synthetic anomalies into the available data. Moreover, our method can effectively take advantage of all the available information, be it as domain knowledge, or as training labels in the semi-supervised setting. We demonstrate empirically on standard benchmark datasets that our approach obtains a state-of-the-art performance in these settings.

Spliced Binned-Pareto Distribution for Robust Modeling of Heavy-tailed Time Series

This work proposes a novel method to robustly and accurately model time series with heavy-tailed noise, in non-stationary scenarios. In many practical application time series have heavy-tailed noise that significantly impacts the performance of classical forecasting models; in particular, accurately modeling a distribution over extreme events is crucial to performing accurate time series anomaly detection. We propose a Spliced Binned-Pareto distribution which is both robust to extreme observations and allows accurate modeling of the full distribution. Our method allows the capture of time dependencies in the higher order moments of the distribution such as the tail heaviness. We compare the robustness and the accuracy of the tail estimation of our method to other state of the art methods on Twitter mentions count time series.

EQuANt (Enhanced Question Answer Network)

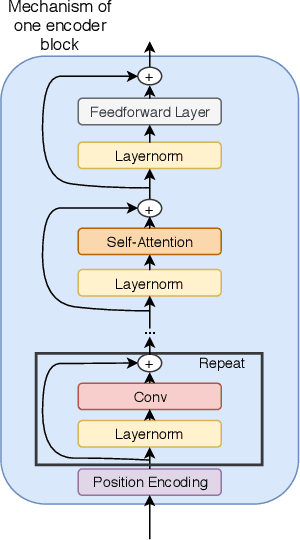
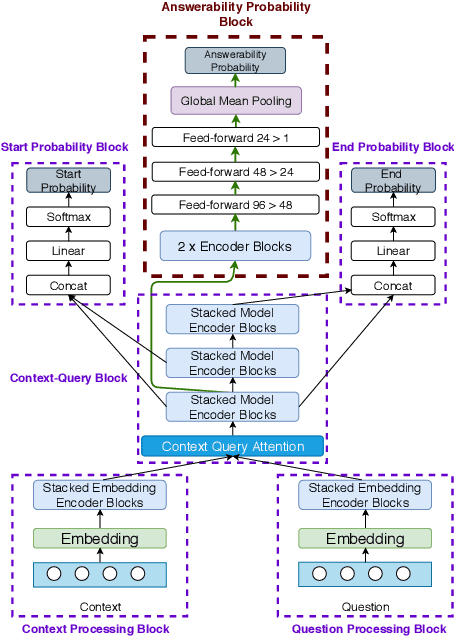
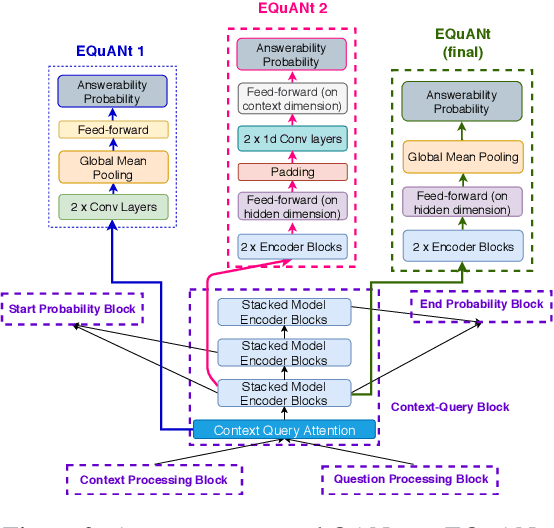
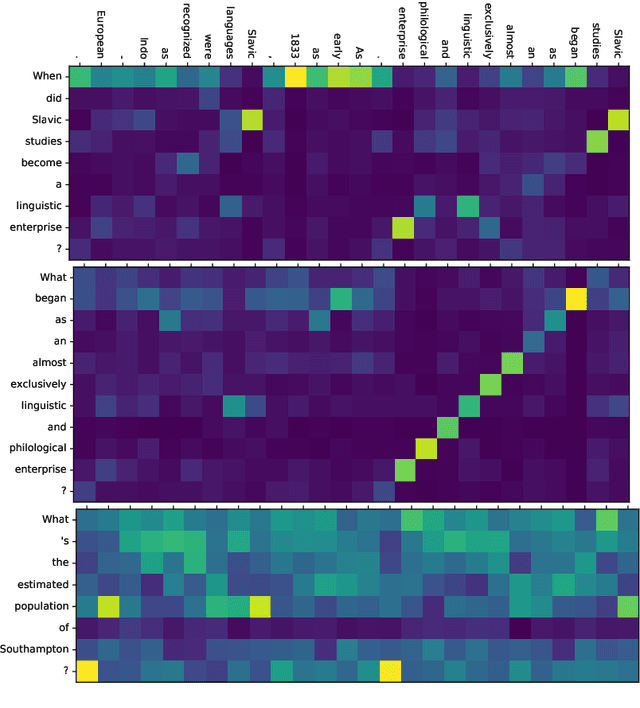
Machine Reading Comprehension (MRC) is an important topic in the domain of automated question answering and in natural language processing more generally. Since the release of the SQuAD 1.1 and SQuAD 2 datasets, progress in the field has been particularly significant, with current state-of-the-art models now exhibiting near-human performance at both answering well-posed questions and detecting questions which are unanswerable given a corresponding context. In this work, we present Enhanced Question Answer Network (EQuANt), an MRC model which extends the successful QANet architecture of Yu et al. to cope with unanswerable questions. By training and evaluating EQuANt on SQuAD 2, we show that it is indeed possible to extend QANet to the unanswerable domain. We achieve results which are close to 2 times better than our chosen baseline obtained by evaluating a lightweight version of the original QANet architecture on SQuAD 2. In addition, we report that the performance of EQuANt on SQuAD 1.1 after being trained on SQuAD2 exceeds that of our lightweight QANet architecture trained and evaluated on SQuAD 1.1, demonstrating the utility of multi-task learning in the MRC context.