Youngsuk Park
Training LLMs with MXFP4
Feb 27, 2025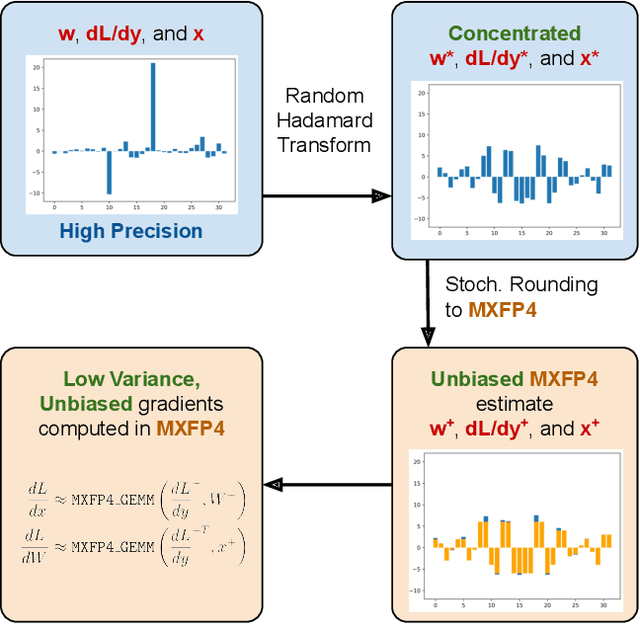

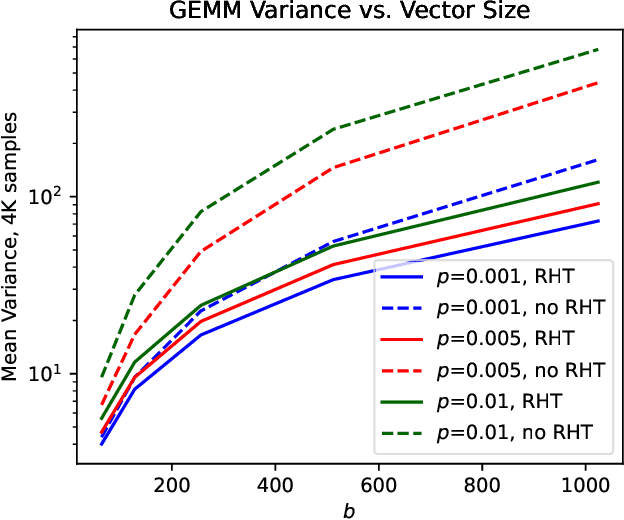
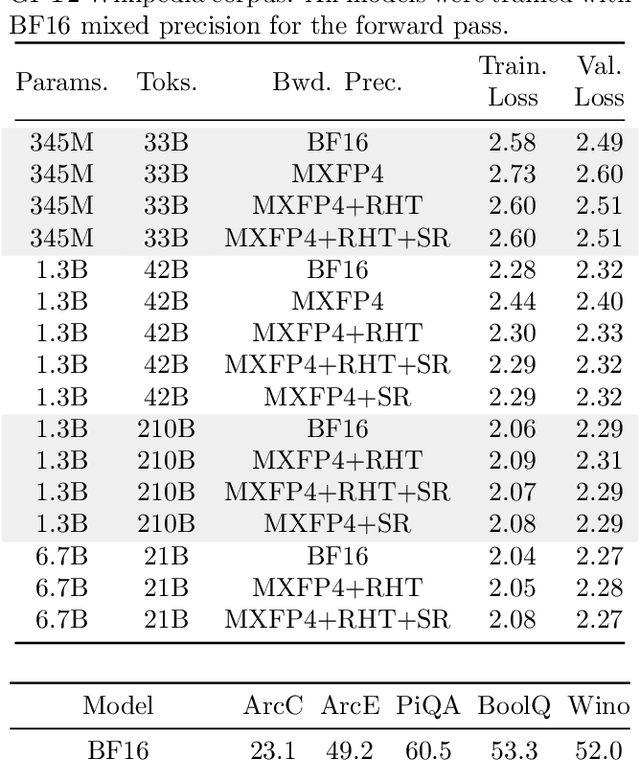
Abstract:Low precision (LP) datatypes such as MXFP4 can accelerate matrix multiplications (GEMMs) and reduce training costs. However, directly using MXFP4 instead of BF16 during training significantly degrades model quality. In this work, we present the first near-lossless training recipe that uses MXFP4 GEMMs, which are $2\times$ faster than FP8 on supported hardware. Our key insight is to compute unbiased gradient estimates with stochastic rounding (SR), resulting in more accurate model updates. However, directly applying SR to MXFP4 can result in high variance from block-level outliers, harming convergence. To overcome this, we use the random Hadamard tranform to theoretically bound the variance of SR. We train GPT models up to 6.7B parameters and find that our method induces minimal degradation over mixed-precision BF16 training. Our recipe computes $>1/2$ the training FLOPs in MXFP4, enabling an estimated speedup of $>1.3\times$ over FP8 and $>1.7\times$ over BF16 during backpropagation.
Stochastic Rounding for LLM Training: Theory and Practice
Feb 27, 2025



Abstract:As the parameters of Large Language Models (LLMs) have scaled to hundreds of billions, the demand for efficient training methods -- balancing faster computation and reduced memory usage without sacrificing accuracy -- has become more critical than ever. In recent years, various mixed precision strategies, which involve different precision levels for optimization components, have been proposed to increase training speed with minimal accuracy degradation. However, these strategies often require manual adjustments and lack theoretical justification. In this work, we leverage stochastic rounding (SR) to address numerical errors of training with low-precision representation. We provide theoretical analyses of implicit regularization and convergence under the Adam optimizer when SR is utilized. With the insights from these analyses, we extend previous BF16 + SR strategy to be used in distributed settings, enhancing the stability and performance for large scale training. Empirical results from pre-training models with up to 6.7B parameters, for the first time, demonstrate that our BF16 with SR strategy outperforms (BF16, FP32) mixed precision strategies, achieving better validation perplexity, up to $1.54\times$ higher throughput, and $30\%$ less memory usage.
RoSTE: An Efficient Quantization-Aware Supervised Fine-Tuning Approach for Large Language Models
Feb 13, 2025Abstract:Supervised fine-tuning is a standard method for adapting pre-trained large language models (LLMs) to downstream tasks. Quantization has been recently studied as a post-training technique for efficient LLM deployment. To obtain quantized fine-tuned LLMs, conventional pipelines would first fine-tune the pre-trained models, followed by post-training quantization. This often yields suboptimal performance as it fails to leverage the synergy between fine-tuning and quantization. To effectively realize low-bit quantization of weights, activations, and KV caches in LLMs, we propose an algorithm named Rotated Straight-Through-Estimator (RoSTE), which combines quantization-aware supervised fine-tuning (QA-SFT) with an adaptive rotation strategy that identifies an effective rotation configuration to reduce activation outliers. We provide theoretical insights on RoSTE by analyzing its prediction error when applied to an overparameterized least square quantized training problem. Our findings reveal that the prediction error is directly proportional to the quantization error of the converged weights, which can be effectively managed through an optimized rotation configuration. Experiments on Pythia and Llama models of different sizes demonstrate the effectiveness of RoSTE. Compared to existing post-SFT quantization baselines, our method consistently achieves superior performances across various tasks and different LLM architectures.
Enhancing Foundation Models for Time Series Forecasting via Wavelet-based Tokenization
Dec 06, 2024



Abstract:How to best develop foundational models for time series forecasting remains an important open question. Tokenization is a crucial consideration in this effort: what is an effective discrete vocabulary for a real-valued sequential input? To address this question, we develop WaveToken, a wavelet-based tokenizer that allows models to learn complex representations directly in the space of time-localized frequencies. Our method first scales and decomposes the input time series, then thresholds and quantizes the wavelet coefficients, and finally pre-trains an autoregressive model to forecast coefficients for the forecast horizon. By decomposing coarse and fine structures in the inputs, wavelets provide an eloquent and compact language for time series forecasting that simplifies learning. Empirical results on a comprehensive benchmark, including 42 datasets for both in-domain and zero-shot settings, show that WaveToken: i) provides better accuracy than recently proposed foundation models for forecasting while using a much smaller vocabulary (1024 tokens), and performs on par or better than modern deep learning models trained specifically on each dataset; and ii) exhibits superior generalization capabilities, achieving the best average rank across all datasets for three complementary metrics. In addition, we show that our method can easily capture complex temporal patterns of practical relevance that are challenging for other recent pre-trained models, including trends, sparse spikes, and non-stationary time series with varying frequencies evolving over time.
Online Posterior Sampling with a Diffusion Prior
Oct 04, 2024
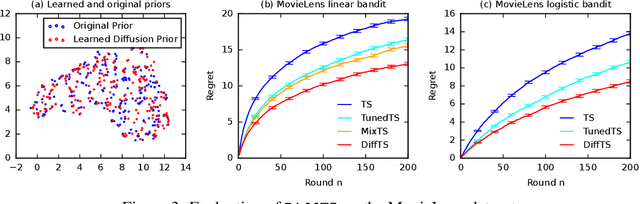


Abstract:Posterior sampling in contextual bandits with a Gaussian prior can be implemented exactly or approximately using the Laplace approximation. The Gaussian prior is computationally efficient but it cannot describe complex distributions. In this work, we propose approximate posterior sampling algorithms for contextual bandits with a diffusion model prior. The key idea is to sample from a chain of approximate conditional posteriors, one for each stage of the reverse process, which are estimated in a closed form using the Laplace approximation. Our approximations are motivated by posterior sampling with a Gaussian prior, and inherit its simplicity and efficiency. They are asymptotically consistent and perform well empirically on a variety of contextual bandit problems.
Inference Optimization of Foundation Models on AI Accelerators
Jul 12, 2024



Abstract:Powerful foundation models, including large language models (LLMs), with Transformer architectures have ushered in a new era of Generative AI across various industries. Industry and research community have witnessed a large number of new applications, based on those foundation models. Such applications include question and answer, customer services, image and video generation, and code completions, among others. However, as the number of model parameters reaches to hundreds of billions, their deployment incurs prohibitive inference costs and high latency in real-world scenarios. As a result, the demand for cost-effective and fast inference using AI accelerators is ever more higher. To this end, our tutorial offers a comprehensive discussion on complementary inference optimization techniques using AI accelerators. Beginning with an overview of basic Transformer architectures and deep learning system frameworks, we deep dive into system optimization techniques for fast and memory-efficient attention computations and discuss how they can be implemented efficiently on AI accelerators. Next, we describe architectural elements that are key for fast transformer inference. Finally, we examine various model compression and fast decoding strategies in the same context.
Collage: Light-Weight Low-Precision Strategy for LLM Training
May 06, 2024



Abstract:Large models training is plagued by the intense compute cost and limited hardware memory. A practical solution is low-precision representation but is troubled by loss in numerical accuracy and unstable training rendering the model less useful. We argue that low-precision floating points can perform well provided the error is properly compensated at the critical locations in the training process. We propose Collage which utilizes multi-component float representation in low-precision to accurately perform operations with numerical errors accounted. To understand the impact of imprecision to training, we propose a simple and novel metric which tracks the lost information during training as well as differentiates various precision strategies. Our method works with commonly used low-precision such as half-precision ($16$-bit floating points) and can be naturally extended to work with even lower precision such as $8$-bit. Experimental results show that pre-training using Collage removes the requirement of using $32$-bit floating-point copies of the model and attains similar/better training performance compared to $(16, 32)$-bit mixed-precision strategy, with up to $3.7\times$ speedup and $\sim 15\%$ to $23\%$ less memory usage in practice.
Variance-reduced Zeroth-Order Methods for Fine-Tuning Language Models
Apr 11, 2024



Abstract:Fine-tuning language models (LMs) has demonstrated success in a wide array of downstream tasks. However, as LMs are scaled up, the memory requirements for backpropagation become prohibitively high. Zeroth-order (ZO) optimization methods can leverage memory-efficient forward passes to estimate gradients. More recently, MeZO, an adaptation of ZO-SGD, has been shown to consistently outperform zero-shot and in-context learning when combined with suitable task prompts. In this work, we couple ZO methods with variance reduction techniques to enhance stability and convergence for inference-based LM fine-tuning. We introduce Memory-Efficient Zeroth-Order Stochastic Variance-Reduced Gradient (MeZO-SVRG) and demonstrate its efficacy across multiple LM fine-tuning tasks, eliminating the reliance on task-specific prompts. Evaluated across a range of both masked and autoregressive LMs on benchmark GLUE tasks, MeZO-SVRG outperforms MeZO with up to 20% increase in test accuracies in both full- and partial-parameter fine-tuning settings. MeZO-SVRG benefits from reduced computation time as it often surpasses MeZO's peak test accuracy with a $2\times$ reduction in GPU-hours. MeZO-SVRG significantly reduces the required memory footprint compared to first-order SGD, i.e. by $2\times$ for autoregressive models. Our experiments highlight that MeZO-SVRG's memory savings progressively improve compared to SGD with larger batch sizes.
Theoretical Guarantees of Learning Ensembling Strategies with Applications to Time Series Forecasting
May 26, 2023



Abstract:Ensembling is among the most popular tools in machine learning (ML) due to its effectiveness in minimizing variance and thus improving generalization. Most ensembling methods for black-box base learners fall under the umbrella of "stacked generalization," namely training an ML algorithm that takes the inferences from the base learners as input. While stacking has been widely applied in practice, its theoretical properties are poorly understood. In this paper, we prove a novel result, showing that choosing the best stacked generalization from a (finite or finite-dimensional) family of stacked generalizations based on cross-validated performance does not perform "much worse" than the oracle best. Our result strengthens and significantly extends the results in Van der Laan et al. (2007). Inspired by the theoretical analysis, we further propose a particular family of stacked generalizations in the context of probabilistic forecasting, each one with a different sensitivity for how much the ensemble weights are allowed to vary across items, timestamps in the forecast horizon, and quantiles. Experimental results demonstrate the performance gain of the proposed method.
Testing Causality for High Dimensional Data
Mar 14, 2023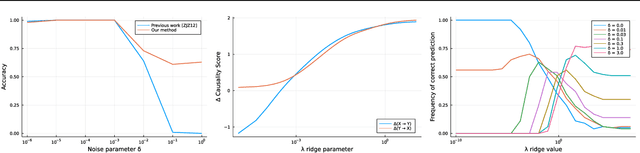
Abstract:Determining causal relationship between high dimensional observations are among the most important tasks in scientific discoveries. In this paper, we revisited the \emph{linear trace method}, a technique proposed in~\citep{janzing2009telling,zscheischler2011testing} to infer the causal direction between two random variables of high dimensions. We strengthen the existing results significantly by providing an improved tail analysis in addition to extending the results to nonlinear trace functionals with sharper confidence bounds under certain distributional assumptions. We obtain our results by interpreting the trace estimator in the causal regime as a function over random orthogonal matrices, where the concentration of Lipschitz functions over such space could be applied. We additionally propose a novel ridge-regularized variant of the estimator in \cite{zscheischler2011testing}, and give provable bounds relating the ridge-estimated terms to their ground-truth counterparts. We support our theoretical results with encouraging experiments on synthetic datasets, more prominently, under high-dimension low sample size regime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge