Closing the Computational-Query Depth Gap in Parallel Stochastic Convex Optimization

We develop a new parallel algorithm for minimizing Lipschitz, convex functions with a stochastic subgradient oracle. The total number of queries made and the query depth, i.e., the number of parallel rounds of queries, match the prior state-of-the-art, [CJJLLST23], while improving upon the computational depth by a polynomial factor for sufficiently small accuracy. When combined with previous state-of-the-art methods our result closes a gap between the best-known query depth and the best-known computational depth of parallel algorithms. Our method starts with a ball acceleration framework of previous parallel methods, i.e., [CJJJLST20, ACJJS21], which reduce the problem to minimizing a regularized Gaussian convolution of the function constrained to Euclidean balls. By developing and leveraging new stability properties of the Hessian of this induced function, we depart from prior parallel algorithms and reduce these ball-constrained optimization problems to stochastic unconstrained quadratic minimization problems. Although we are unable to prove concentration of the asymmetric matrices that we use to approximate this Hessian, we nevertheless develop an efficient parallel method for solving these quadratics. Interestingly, our algorithms can be improved using fast matrix multiplication and use nearly-linear work if the matrix multiplication exponent is 2.

Black-Box $k$-to-$1$-PCA Reductions: Theory and Applications

The $k$-principal component analysis ($k$-PCA) problem is a fundamental algorithmic primitive that is widely-used in data analysis and dimensionality reduction applications. In statistical settings, the goal of $k$-PCA is to identify a top eigenspace of the covariance matrix of a distribution, which we only have implicit access to via samples. Motivated by these implicit settings, we analyze black-box deflation methods as a framework for designing $k$-PCA algorithms, where we model access to the unknown target matrix via a black-box $1$-PCA oracle which returns an approximate top eigenvector, under two popular notions of approximation. Despite being arguably the most natural reduction-based approach to $k$-PCA algorithm design, such black-box methods, which recursively call a $1$-PCA oracle $k$ times, were previously poorly-understood. Our main contribution is significantly sharper bounds on the approximation parameter degradation of deflation methods for $k$-PCA. For a quadratic form notion of approximation we term ePCA (energy PCA), we show deflation methods suffer no parameter loss. For an alternative well-studied approximation notion we term cPCA (correlation PCA), we tightly characterize the parameter regimes where deflation methods are feasible. Moreover, we show that in all feasible regimes, $k$-cPCA deflation algorithms suffer no asymptotic parameter loss for any constant $k$. We apply our framework to obtain state-of-the-art $k$-PCA algorithms robust to dataset contamination, improving prior work both in sample complexity and approximation quality.

A Whole New Ball Game: A Primal Accelerated Method for Matrix Games and Minimizing the Maximum of Smooth Functions

We design algorithms for minimizing $\max_{i\in[n]} f_i(x)$ over a $d$-dimensional Euclidean or simplex domain. When each $f_i$ is $1$-Lipschitz and $1$-smooth, our method computes an $\epsilon$-approximate solution using $\widetilde{O}(n \epsilon^{-1/3} + \epsilon^{-2})$ gradient and function evaluations, and $\widetilde{O}(n \epsilon^{-4/3})$ additional runtime. For large $n$, our evaluation complexity is optimal up to polylogarithmic factors. In the special case where each $f_i$ is linear -- which corresponds to finding a near-optimal primal strategy in a matrix game -- our method finds an $\epsilon$-approximate solution in runtime $\widetilde{O}(n (d/\epsilon)^{2/3} + nd + d\epsilon^{-2})$. For $n>d$ and $\epsilon=1/\sqrt{n}$ this improves over all existing first-order methods. When additionally $d = \omega(n^{8/11})$ our runtime also improves over all known interior point methods. Our algorithm combines three novel primitives: (1) A dynamic data structure which enables efficient stochastic gradient estimation in small $\ell_2$ or $\ell_1$ balls. (2) A mirror descent algorithm tailored to our data structure implementing an oracle which minimizes the objective over these balls. (3) A simple ball oracle acceleration framework suitable for non-Euclidean geometry.

Structured Semidefinite Programming for Recovering Structured Preconditioners

We develop a general framework for finding approximately-optimal preconditioners for solving linear systems. Leveraging this framework we obtain improved runtimes for fundamental preconditioning and linear system solving problems including the following. We give an algorithm which, given positive definite $\mathbf{K} \in \mathbb{R}^{d \times d}$ with $\mathrm{nnz}(\mathbf{K})$ nonzero entries, computes an $\epsilon$-optimal diagonal preconditioner in time $\widetilde{O}(\mathrm{nnz}(\mathbf{K}) \cdot \mathrm{poly}(\kappa^\star,\epsilon^{-1}))$, where $\kappa^\star$ is the optimal condition number of the rescaled matrix. We give an algorithm which, given $\mathbf{M} \in \mathbb{R}^{d \times d}$ that is either the pseudoinverse of a graph Laplacian matrix or a constant spectral approximation of one, solves linear systems in $\mathbf{M}$ in $\widetilde{O}(d^2)$ time. Our diagonal preconditioning results improve state-of-the-art runtimes of $\Omega(d^{3.5})$ attained by general-purpose semidefinite programming, and our solvers improve state-of-the-art runtimes of $\Omega(d^{\omega})$ where $\omega > 2.3$ is the current matrix multiplication constant. We attain our results via new algorithms for a class of semidefinite programs (SDPs) we call matrix-dictionary approximation SDPs, which we leverage to solve an associated problem we call matrix-dictionary recovery.

Testing Causality for High Dimensional Data

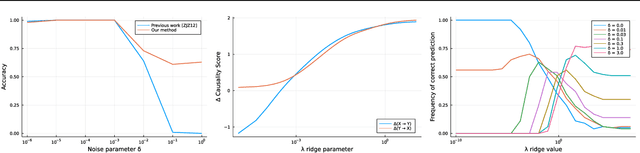
Determining causal relationship between high dimensional observations are among the most important tasks in scientific discoveries. In this paper, we revisited the \emph{linear trace method}, a technique proposed in~\citep{janzing2009telling,zscheischler2011testing} to infer the causal direction between two random variables of high dimensions. We strengthen the existing results significantly by providing an improved tail analysis in addition to extending the results to nonlinear trace functionals with sharper confidence bounds under certain distributional assumptions. We obtain our results by interpreting the trace estimator in the causal regime as a function over random orthogonal matrices, where the concentration of Lipschitz functions over such space could be applied. We additionally propose a novel ridge-regularized variant of the estimator in \cite{zscheischler2011testing}, and give provable bounds relating the ridge-estimated terms to their ground-truth counterparts. We support our theoretical results with encouraging experiments on synthetic datasets, more prominently, under high-dimension low sample size regime.

ReSQueing Parallel and Private Stochastic Convex Optimization

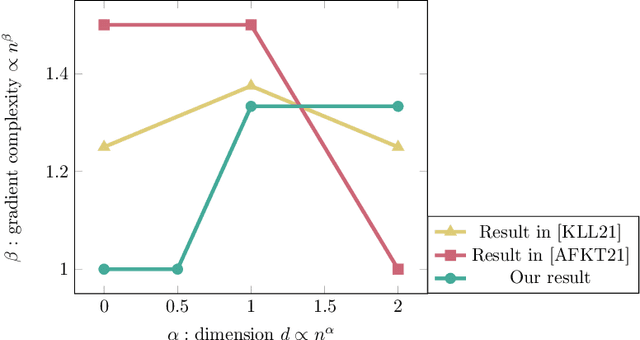
We introduce a new tool for stochastic convex optimization (SCO): a Reweighted Stochastic Query (ReSQue) estimator for the gradient of a function convolved with a (Gaussian) probability density. Combining ReSQue with recent advances in ball oracle acceleration [CJJJLST20, ACJJS21], we develop algorithms achieving state-of-the-art complexities for SCO in parallel and private settings. For a SCO objective constrained to the unit ball in $\mathbb{R}^d$, we obtain the following results (up to polylogarithmic factors). We give a parallel algorithm obtaining optimization error $\epsilon_{\text{opt}}$ with $d^{1/3}\epsilon_{\text{opt}}^{-2/3}$ gradient oracle query depth and $d^{1/3}\epsilon_{\text{opt}}^{-2/3} + \epsilon_{\text{opt}}^{-2}$ gradient queries in total, assuming access to a bounded-variance stochastic gradient estimator. For $\epsilon_{\text{opt}} \in [d^{-1}, d^{-1/4}]$, our algorithm matches the state-of-the-art oracle depth of [BJLLS19] while maintaining the optimal total work of stochastic gradient descent. We give an $(\epsilon_{\text{dp}}, \delta)$-differentially private algorithm which, given $n$ samples of Lipschitz loss functions, obtains near-optimal optimization error and makes $\min(n, n^2\epsilon_{\text{dp}}^2 d^{-1}) + \min(n^{4/3}\epsilon_{\text{dp}}^{1/3}, (nd)^{2/3}\epsilon_{\text{dp}}^{-1})$ queries to the gradients of these functions. In the regime $d \le n \epsilon_{\text{dp}}^{2}$, where privacy comes at no cost in terms of the optimal loss up to constants, our algorithm uses $n + (nd)^{2/3}\epsilon_{\text{dp}}^{-1}$ queries and improves recent advancements of [KLL21, AFKT21]. In the moderately low-dimensional setting $d \le \sqrt n \epsilon_{\text{dp}}^{3/2}$, our query complexity is near-linear.

RECAPP: Crafting a More Efficient Catalyst for Convex Optimization

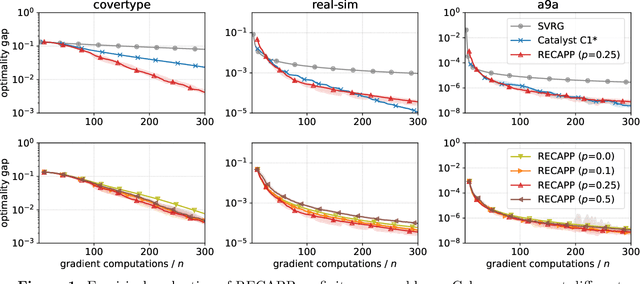
The accelerated proximal point algorithm (APPA), also known as "Catalyst", is a well-established reduction from convex optimization to approximate proximal point computation (i.e., regularized minimization). This reduction is conceptually elegant and yields strong convergence rate guarantees. However, these rates feature an extraneous logarithmic term arising from the need to compute each proximal point to high accuracy. In this work, we propose a novel Relaxed Error Criterion for Accelerated Proximal Point (RECAPP) that eliminates the need for high accuracy subproblem solutions. We apply RECAPP to two canonical problems: finite-sum and max-structured minimization. For finite-sum problems, we match the best known complexity, previously obtained by carefully-designed problem-specific algorithms. For minimizing $\max_y f(x,y)$ where $f$ is convex in $x$ and strongly-concave in $y$, we improve on the best known (Catalyst-based) bound by a logarithmic factor.

Robust Regression Revisited: Acceleration and Improved Estimation Rates

We study fast algorithms for statistical regression problems under the strong contamination model, where the goal is to approximately optimize a generalized linear model (GLM) given adversarially corrupted samples. Prior works in this line of research were based on the robust gradient descent framework of Prasad et. al., a first-order method using biased gradient queries, or the Sever framework of Diakonikolas et. al., an iterative outlier-removal method calling a stationary point finder. We present nearly-linear time algorithms for robust regression problems with improved runtime or estimation guarantees compared to the state-of-the-art. For the general case of smooth GLMs (e.g. logistic regression), we show that the robust gradient descent framework of Prasad et. al. can be accelerated, and show our algorithm extends to optimizing the Moreau envelopes of Lipschitz GLMs (e.g. support vector machines), answering several open questions in the literature. For the well-studied case of robust linear regression, we present an alternative approach obtaining improved estimation rates over prior nearly-linear time algorithms. Interestingly, our method starts with an identifiability proof introduced in the context of the sum-of-squares algorithm of Bakshi and Prasad, which achieved optimal error rates while requiring large polynomial runtime and sample complexity. We reinterpret their proof within the Sever framework and obtain a dramatically faster and more sample-efficient algorithm under fewer distributional assumptions.

Stochastic Bias-Reduced Gradient Methods

We develop a new primitive for stochastic optimization: a low-bias, low-cost estimator of the minimizer $x_\star$ of any Lipschitz strongly-convex function. In particular, we use a multilevel Monte-Carlo approach due to Blanchet and Glynn to turn any optimal stochastic gradient method into an estimator of $x_\star$ with bias $\delta$, variance $O(\log(1/\delta))$, and an expected sampling cost of $O(\log(1/\delta))$ stochastic gradient evaluations. As an immediate consequence, we obtain cheap and nearly unbiased gradient estimators for the Moreau-Yoshida envelope of any Lipschitz convex function, allowing us to perform dimension-free randomized smoothing. We demonstrate the potential of our estimator through four applications. First, we develop a method for minimizing the maximum of $N$ functions, improving on recent results and matching a lower bound up logarithmic factors. Second and third, we recover state-of-the-art rates for projection-efficient and gradient-efficient optimization using simple algorithms with a transparent analysis. Finally, we show that an improved version of our estimator would yield a nearly linear-time, optimal-utility, differentially-private non-smooth stochastic optimization method.

Thinking Inside the Ball: Near-Optimal Minimization of the Maximal Loss

We characterize the complexity of minimizing $\max_{i\in[N]} f_i(x)$ for convex, Lipschitz functions $f_1,\ldots, f_N$. For non-smooth functions, existing methods require $O(N\epsilon^{-2})$ queries to a first-order oracle to compute an $\epsilon$-suboptimal point and $\tilde{O}(N\epsilon^{-1})$ queries if the $f_i$ are $O(1/\epsilon)$-smooth. We develop methods with improved complexity bounds of $\tilde{O}(N\epsilon^{-2/3} + \epsilon^{-8/3})$ in the non-smooth case and $\tilde{O}(N\epsilon^{-2/3} + \sqrt{N}\epsilon^{-1})$ in the $O(1/\epsilon)$-smooth case. Our methods consist of a recently proposed ball optimization oracle acceleration algorithm (which we refine) and a careful implementation of said oracle for the softmax function. We also prove an oracle complexity lower bound scaling as $\Omega(N\epsilon^{-2/3})$, showing that our dependence on $N$ is optimal up to polylogarithmic factors.