Learning Mixtures of Unknown Causal Interventions

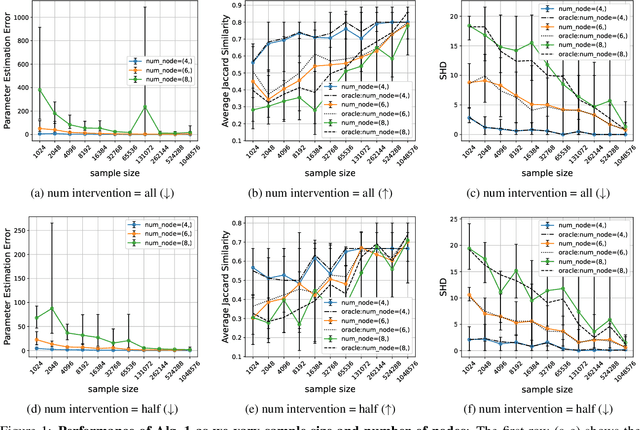
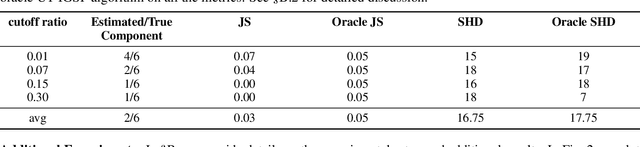
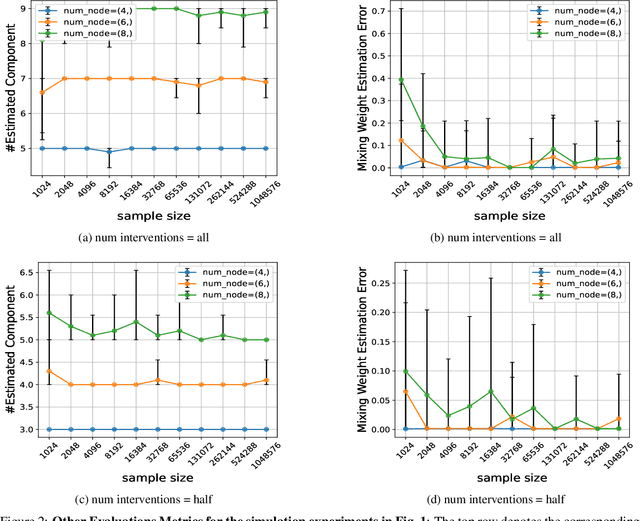
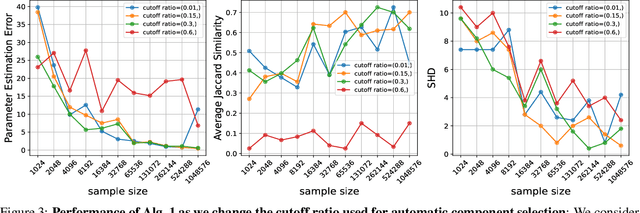
The ability to conduct interventions plays a pivotal role in learning causal relationships among variables, thus facilitating applications across diverse scientific disciplines such as genomics, economics, and machine learning. However, in many instances within these applications, the process of generating interventional data is subject to noise: rather than data being sampled directly from the intended interventional distribution, interventions often yield data sampled from a blend of both intended and unintended interventional distributions. We consider the fundamental challenge of disentangling mixed interventional and observational data within linear Structural Equation Models (SEMs) with Gaussian additive noise without the knowledge of the true causal graph. We demonstrate that conducting interventions, whether do or soft, yields distributions with sufficient diversity and properties conducive to efficiently recovering each component within the mixture. Furthermore, we establish that the sample complexity required to disentangle mixed data inversely correlates with the extent of change induced by an intervention in the equations governing the affected variable values. As a result, the causal graph can be identified up to its interventional Markov Equivalence Class, similar to scenarios where no noise influences the generation of interventional data. We further support our theoretical findings by conducting simulations wherein we perform causal discovery from such mixed data.

Causal Discovery with Fewer Conditional Independence Tests

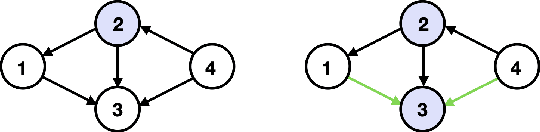
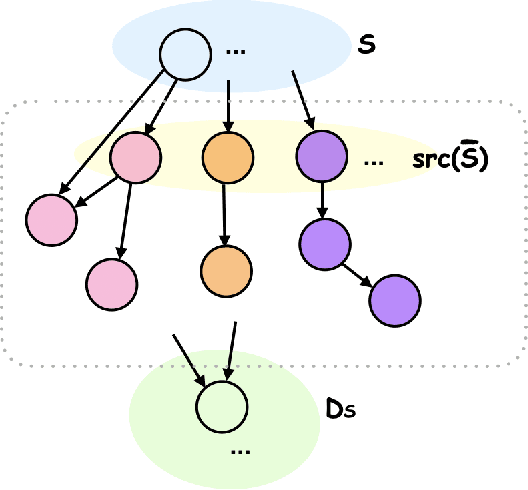
Many questions in science center around the fundamental problem of understanding causal relationships. However, most constraint-based causal discovery algorithms, including the well-celebrated PC algorithm, often incur an exponential number of conditional independence (CI) tests, posing limitations in various applications. Addressing this, our work focuses on characterizing what can be learned about the underlying causal graph with a reduced number of CI tests. We show that it is possible to a learn a coarser representation of the hidden causal graph with a polynomial number of tests. This coarser representation, named Causal Consistent Partition Graph (CCPG), comprises of a partition of the vertices and a directed graph defined over its components. CCPG satisfies consistency of orientations and additional constraints which favor finer partitions. Furthermore, it reduces to the underlying causal graph when the causal graph is identifiable. As a consequence, our results offer the first efficient algorithm for recovering the true causal graph with a polynomial number of tests, in special cases where the causal graph is fully identifiable through observational data and potentially additional interventions.

Quantifying the Gain in Weak-to-Strong Generalization

Recent advances in large language models have shown capabilities that are extraordinary and near-superhuman. These models operate with such complexity that reliably evaluating and aligning them proves challenging for humans. This leads to the natural question: can guidance from weak models (like humans) adequately direct the capabilities of strong models? In a recent and somewhat surprising work, Burns et al. (2023) empirically demonstrated that when strong models (like GPT-4) are finetuned using labels generated by weak supervisors (like GPT-2), the strong models outperform their weaker counterparts -- a phenomenon they term weak-to-strong generalization. In this work, we present a theoretical framework for understanding weak-to-strong generalization. Specifically, we show that the improvement in performance achieved by strong models over their weaker counterparts is quantified by the misfit error incurred by the strong model on labels generated by the weaker model. Our theory reveals several curious algorithmic insights. For instance, we can predict the amount by which the strong model will improve over the weak model, and also choose among different weak models to train the strong model, based on its misfit error. We validate our theoretical findings through various empirical assessments.

Membership Testing in Markov Equivalence Classes via Independence Query Oracles

Understanding causal relationships between variables is a fundamental problem with broad impact in numerous scientific fields. While extensive research has been dedicated to learning causal graphs from data, its complementary concept of testing causal relationships has remained largely unexplored. While learning involves the task of recovering the Markov equivalence class (MEC) of the underlying causal graph from observational data, the testing counterpart addresses the following critical question: Given a specific MEC and observational data from some causal graph, can we determine if the data-generating causal graph belongs to the given MEC? We explore constraint-based testing methods by establishing bounds on the required number of conditional independence tests. Our bounds are in terms of the size of the maximum undirected clique ($s$) of the given MEC. In the worst case, we show a lower bound of $\exp(\Omega(s))$ independence tests. We then give an algorithm that resolves the task with $\exp(O(s))$ tests, matching our lower bound. Compared to the learning problem, where algorithms often use a number of independence tests that is exponential in the maximum in-degree, this shows that testing is relatively easier. In particular, it requires exponentially less independence tests in graphs featuring high in-degrees and small clique sizes. Additionally, using the DAG associahedron, we provide a geometric interpretation of testing versus learning and discuss how our testing result can aid learning.

Causal Discovery under Off-Target Interventions

Causal graph discovery is a significant problem with applications across various disciplines. However, with observational data alone, the underlying causal graph can only be recovered up to its Markov equivalence class, and further assumptions or interventions are necessary to narrow down the true graph. This work addresses the causal discovery problem under the setting of stochastic interventions with the natural goal of minimizing the number of interventions performed. We propose the following stochastic intervention model which subsumes existing adaptive noiseless interventions in the literature while capturing scenarios such as fat-hand interventions and CRISPR gene knockouts: any intervention attempt results in an actual intervention on a random subset of vertices, drawn from a distribution dependent on attempted action. Under this model, we study the two fundamental problems in causal discovery of verification and search and provide approximation algorithms with polylogarithmic competitive ratios and provide some preliminary experimental results.

Testing with Non-identically Distributed Samples

We examine the extent to which sublinear-sample property testing and estimation applies to settings where samples are independently but not identically distributed. Specifically, we consider the following distributional property testing framework: Suppose there is a set of distributions over a discrete support of size $k$, $\textbf{p}_1, \textbf{p}_2,\ldots,\textbf{p}_T$, and we obtain $c$ independent draws from each distribution. Suppose the goal is to learn or test a property of the average distribution, $\textbf{p}_{\mathrm{avg}}$. This setup models a number of important practical settings where the individual distributions correspond to heterogeneous entities -- either individuals, chronologically distinct time periods, spatially separated data sources, etc. From a learning standpoint, even with $c=1$ samples from each distribution, $\Theta(k/\varepsilon^2)$ samples are necessary and sufficient to learn $\textbf{p}_{\mathrm{avg}}$ to within error $\varepsilon$ in TV distance. To test uniformity or identity -- distinguishing the case that $\textbf{p}_{\mathrm{avg}}$ is equal to some reference distribution, versus has $\ell_1$ distance at least $\varepsilon$ from the reference distribution, we show that a linear number of samples in $k$ is necessary given $c=1$ samples from each distribution. In contrast, for $c \ge 2$, we recover the usual sublinear sample testing of the i.i.d. setting: we show that $O(\sqrt{k}/\varepsilon^2 + 1/\varepsilon^4)$ samples are sufficient, matching the optimal sample complexity in the i.i.d. case in the regime where $\varepsilon \ge k^{-1/4}$. Additionally, we show that in the $c=2$ case, there is a constant $\rho > 0$ such that even in the linear regime with $\rho k$ samples, no tester that considers the multiset of samples (ignoring which samples were drawn from the same $\textbf{p}_i$) can perform uniformity testing.

Meek Separators and Their Applications in Targeted Causal Discovery

Learning causal structures from interventional data is a fundamental problem with broad applications across various fields. While many previous works have focused on recovering the entire causal graph, in practice, there are scenarios where learning only part of the causal graph suffices. This is called $targeted$ causal discovery. In our work, we focus on two such well-motivated problems: subset search and causal matching. We aim to minimize the number of interventions in both cases. Towards this, we introduce the $Meek~separator$, which is a subset of vertices that, when intervened, decomposes the remaining unoriented edges into smaller connected components. We then present an efficient algorithm to find Meek separators that are of small sizes. Such a procedure is helpful in designing various divide-and-conquer-based approaches. In particular, we propose two randomized algorithms that achieve logarithmic approximation for subset search and causal matching, respectively. Our results provide the first known average-case provable guarantees for both problems. We believe that this opens up possibilities to design near-optimal methods for many other targeted causal structure learning problems arising from various applications.

Structured Semidefinite Programming for Recovering Structured Preconditioners

We develop a general framework for finding approximately-optimal preconditioners for solving linear systems. Leveraging this framework we obtain improved runtimes for fundamental preconditioning and linear system solving problems including the following. We give an algorithm which, given positive definite $\mathbf{K} \in \mathbb{R}^{d \times d}$ with $\mathrm{nnz}(\mathbf{K})$ nonzero entries, computes an $\epsilon$-optimal diagonal preconditioner in time $\widetilde{O}(\mathrm{nnz}(\mathbf{K}) \cdot \mathrm{poly}(\kappa^\star,\epsilon^{-1}))$, where $\kappa^\star$ is the optimal condition number of the rescaled matrix. We give an algorithm which, given $\mathbf{M} \in \mathbb{R}^{d \times d}$ that is either the pseudoinverse of a graph Laplacian matrix or a constant spectral approximation of one, solves linear systems in $\mathbf{M}$ in $\widetilde{O}(d^2)$ time. Our diagonal preconditioning results improve state-of-the-art runtimes of $\Omega(d^{3.5})$ attained by general-purpose semidefinite programming, and our solvers improve state-of-the-art runtimes of $\Omega(d^{\omega})$ where $\omega > 2.3$ is the current matrix multiplication constant. We attain our results via new algorithms for a class of semidefinite programs (SDPs) we call matrix-dictionary approximation SDPs, which we leverage to solve an associated problem we call matrix-dictionary recovery.

Adaptivity Complexity for Causal Graph Discovery

Causal discovery from interventional data is an important problem, where the task is to design an interventional strategy that learns the hidden ground truth causal graph $G(V,E)$ on $|V| = n$ nodes while minimizing the number of performed interventions. Most prior interventional strategies broadly fall into two categories: non-adaptive and adaptive. Non-adaptive strategies decide on a single fixed set of interventions to be performed while adaptive strategies can decide on which nodes to intervene on sequentially based on past interventions. While adaptive algorithms may use exponentially fewer interventions than their non-adaptive counterparts, there are practical concerns that constrain the amount of adaptivity allowed. Motivated by this trade-off, we study the problem of $r$-adaptivity, where the algorithm designer recovers the causal graph under a total of $r$ sequential rounds whilst trying to minimize the total number of interventions. For this problem, we provide a $r$-adaptive algorithm that achieves $O(\min\{r,\log n\} \cdot n^{1/\min\{r,\log n\}})$ approximation with respect to the verification number, a well-known lower bound for adaptive algorithms. Furthermore, for every $r$, we show that our approximation is tight. Our definition of $r$-adaptivity interpolates nicely between the non-adaptive ($r=1$) and fully adaptive ($r=n$) settings where our approximation simplifies to $O(n)$ and $O(\log n)$ respectively, matching the best-known approximation guarantees for both extremes. Our results also extend naturally to the bounded size interventions.

New metrics and search algorithms for weighted causal DAGs

Recovering causal relationships from data is an important problem. Using observational data, one can typically only recover causal graphs up to a Markov equivalence class and additional assumptions or interventional data are needed for complete recovery. In this work, under some standard assumptions, we study causal graph discovery via adaptive interventions with node-dependent interventional costs. For this setting, we show that no algorithm can achieve an approximation guarantee that is asymptotically better than linear in the number of vertices with respect to the verification number; a well-established benchmark for adaptive search algorithms. Motivated by this negative result, we define a new benchmark that captures the worst-case interventional cost for any search algorithm. Furthermore, with respect to this new benchmark, we provide adaptive search algorithms that achieve logarithmic approximations under various settings: atomic, bounded size interventions and generalized cost objectives.