Endless Terminals: Scaling RL Environments for Terminal Agents

Environments are the bottleneck for self-improving agents. Current terminal benchmarks were built for evaluation, not training; reinforcement learning requires a scalable pipeline, not just a dataset. We introduce Endless Terminals, a fully autonomous pipeline that procedurally generates terminal-use tasks without human annotation. The pipeline has four stages: generating diverse task descriptions, building and validating containerized environments, producing completion tests, and filtering for solvability. From this pipeline we obtain 3255 tasks spanning file operations, log management, data processing, scripting, and database operations. We train agents using vanilla PPO with binary episode level rewards and a minimal interaction loop: no retrieval, multi-agent coordination, or specialized tools. Despite this simplicity, models trained on Endless Terminals show substantial gains: on our held-out dev set, Llama-3.2-3B improves from 4.0% to 18.2%, Qwen2.5-7B from 10.7% to 53.3%, and Qwen3-8B-openthinker-sft from 42.6% to 59.0%. These improvements transfer to human-curated benchmarks: models trained on Endless Terminals show substantial gains on held out human curated benchmarks: on TerminalBench 2.0, Llama-3.2-3B improves from 0.0% to 2.2%, Qwen2.5-7B from 2.2% to 3.4%, and Qwen3-8B-openthinker-sft from 1.1% to 6.7%, in each case outperforming alternative approaches including models with more complex agentic scaffolds. These results demonstrate that simple RL succeeds when environments scale.

Wait, Wait, Wait... Why Do Reasoning Models Loop?

Reasoning models (e.g., DeepSeek-R1) generate long chains of thought to solve harder problems, but they often loop, repeating the same text at low temperatures or with greedy decoding. We study why this happens and what role temperature plays. With open reasoning models, we find that looping is common at low temperature. Larger models tend to loop less, and distilled students loop significantly even when their teachers rarely do. This points to mismatches between the training distribution and the learned model, which we refer to as errors in learning, as a key cause. To understand how such errors cause loops, we introduce a synthetic graph reasoning task and demonstrate two mechanisms. First, risk aversion caused by hardness of learning: when the correct progress-making action is hard to learn but an easy cyclic action is available, the model puts relatively more probability on the cyclic action and gets stuck. Second, even when there is no hardness, Transformers show an inductive bias toward temporally correlated errors, so the same few actions keep being chosen and loops appear. Higher temperature reduces looping by promoting exploration, but it does not fix the errors in learning, so generations remain much longer than necessary at high temperature; in this sense, temperature is a stopgap rather than a holistic solution. We end with a discussion of training-time interventions aimed at directly reducing errors in learning.

Inference-Time Scaling for Complex Tasks: Where We Stand and What Lies Ahead

Inference-time scaling can enhance the reasoning capabilities of large language models (LLMs) on complex problems that benefit from step-by-step problem solving. Although lengthening generated scratchpads has proven effective for mathematical tasks, the broader impact of this approach on other tasks remains less clear. In this work, we investigate the benefits and limitations of scaling methods across nine state-of-the-art models and eight challenging tasks, including math and STEM reasoning, calendar planning, NP-hard problems, navigation, and spatial reasoning. We compare conventional models (e.g., GPT-4o) with models fine-tuned for inference-time scaling (e.g., o1) through evaluation protocols that involve repeated model calls, either independently or sequentially with feedback. These evaluations approximate lower and upper performance bounds and potential for future performance improvements for each model, whether through enhanced training or multi-model inference systems. Our extensive empirical analysis reveals that the advantages of inference-time scaling vary across tasks and diminish as problem complexity increases. In addition, simply using more tokens does not necessarily translate to higher accuracy in these challenging regimes. Results from multiple independent runs with conventional models using perfect verifiers show that, for some tasks, these models can achieve performance close to the average performance of today's most advanced reasoning models. However, for other tasks, a significant performance gap remains, even in very high scaling regimes. Encouragingly, all models demonstrate significant gains when inference is further scaled with perfect verifiers or strong feedback, suggesting ample potential for future improvements.

Discovering Data Structures: Nearest Neighbor Search and Beyond

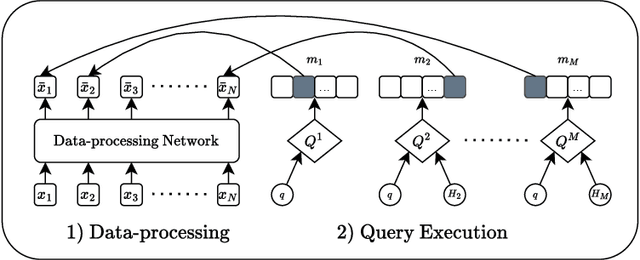
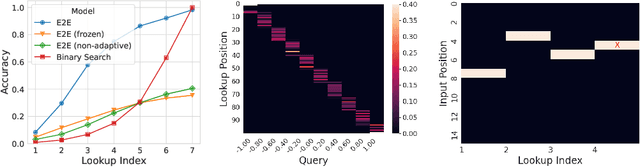
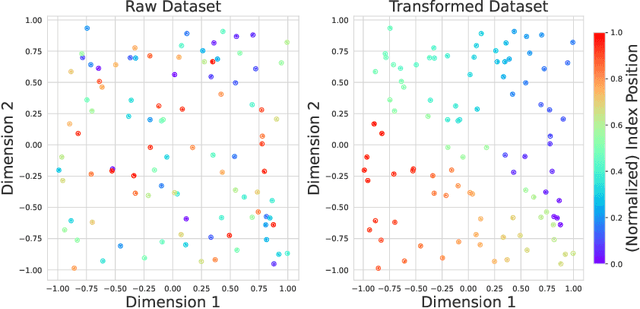
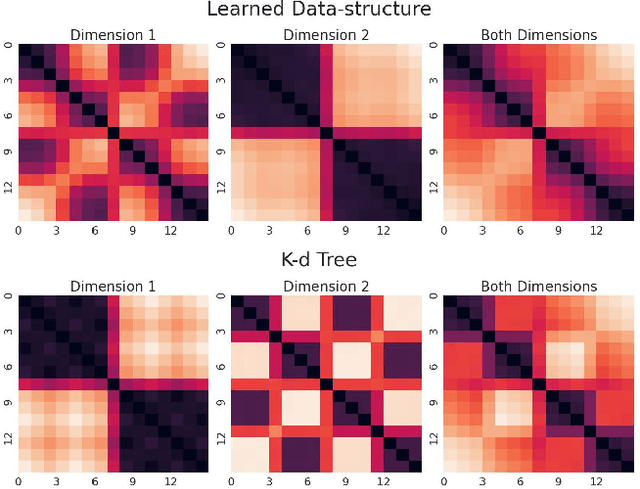
We propose a general framework for end-to-end learning of data structures. Our framework adapts to the underlying data distribution and provides fine-grained control over query and space complexity. Crucially, the data structure is learned from scratch, and does not require careful initialization or seeding with candidate data structures/algorithms. We first apply this framework to the problem of nearest neighbor search. In several settings, we are able to reverse-engineer the learned data structures and query algorithms. For 1D nearest neighbor search, the model discovers optimal distribution (in)dependent algorithms such as binary search and variants of interpolation search. In higher dimensions, the model learns solutions that resemble k-d trees in some regimes, while in others, they have elements of locality-sensitive hashing. The model can also learn useful representations of high-dimensional data and exploit them to design effective data structures. We also adapt our framework to the problem of estimating frequencies over a data stream, and believe it could also be a powerful discovery tool for new problems.

Attribute-to-Delete: Machine Unlearning via Datamodel Matching

Machine unlearning -- efficiently removing the effect of a small "forget set" of training data on a pre-trained machine learning model -- has recently attracted significant research interest. Despite this interest, however, recent work shows that existing machine unlearning techniques do not hold up to thorough evaluation in non-convex settings. In this work, we introduce a new machine unlearning technique that exhibits strong empirical performance even in such challenging settings. Our starting point is the perspective that the goal of unlearning is to produce a model whose outputs are statistically indistinguishable from those of a model re-trained on all but the forget set. This perspective naturally suggests a reduction from the unlearning problem to that of data attribution, where the goal is to predict the effect of changing the training set on a model's outputs. Thus motivated, we propose the following meta-algorithm, which we call Datamodel Matching (DMM): given a trained model, we (a) use data attribution to predict the output of the model if it were re-trained on all but the forget set points; then (b) fine-tune the pre-trained model to match these predicted outputs. In a simple convex setting, we show how this approach provably outperforms a variety of iterative unlearning algorithms. Empirically, we use a combination of existing evaluations and a new metric based on the KL-divergence to show that even in non-convex settings, DMM achieves strong unlearning performance relative to existing algorithms. An added benefit of DMM is that it is a meta-algorithm, in the sense that future advances in data attribution translate directly into better unlearning algorithms, pointing to a clear direction for future progress in unlearning.

Pipe Routing with Topology Control for UAV Networks

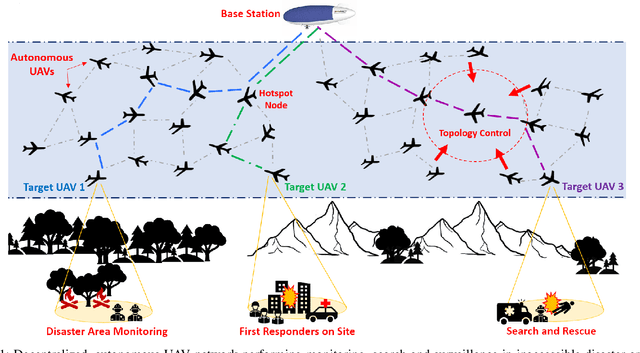
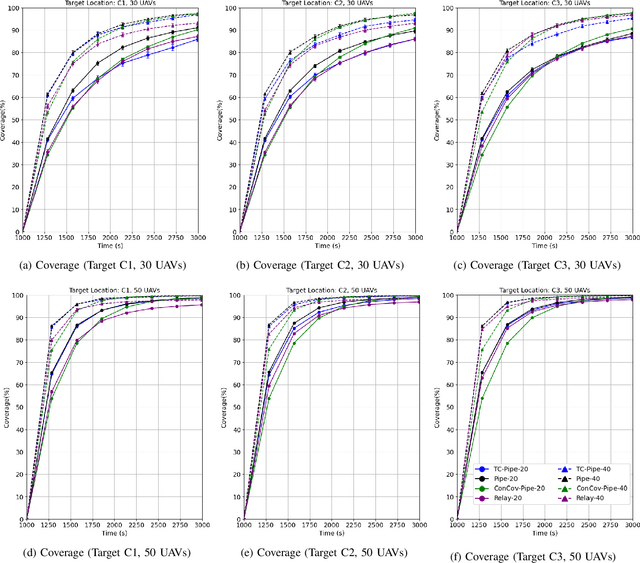
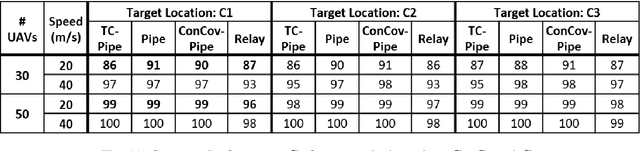
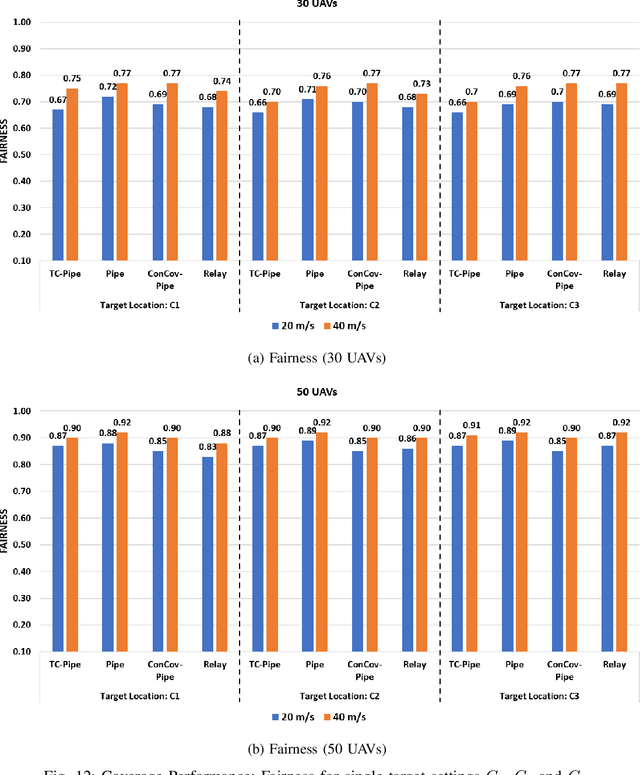
Routing protocols help in transmitting the sensed data from UAVs monitoring the targets (called target UAVs) to the BS. However, the highly dynamic nature of an autonomous, decentralized UAV network leads to frequent route breaks or traffic disruptions. Traditional routing schemes cannot quickly adapt to dynamic UAV networks and/or incur large control overhead and delays. To establish stable, high-quality routes from target UAVs to the BS, we design a hybrid reactive routing scheme called pipe routing that is mobility, congestion, and energy-aware. The pipe routing scheme discovers routes on-demand and proactively switches to alternate high-quality routes within a limited region around the active routes (called the pipe) when needed, reducing the number of route breaks and increasing data throughput. We then design a novel topology control-based pipe routing scheme to maintain robust connectivity in the pipe region around the active routes, leading to improved route stability and increased throughput with minimal impact on the coverage performance of the UAV network.

Testing with Non-identically Distributed Samples

We examine the extent to which sublinear-sample property testing and estimation applies to settings where samples are independently but not identically distributed. Specifically, we consider the following distributional property testing framework: Suppose there is a set of distributions over a discrete support of size $k$, $\textbf{p}_1, \textbf{p}_2,\ldots,\textbf{p}_T$, and we obtain $c$ independent draws from each distribution. Suppose the goal is to learn or test a property of the average distribution, $\textbf{p}_{\mathrm{avg}}$. This setup models a number of important practical settings where the individual distributions correspond to heterogeneous entities -- either individuals, chronologically distinct time periods, spatially separated data sources, etc. From a learning standpoint, even with $c=1$ samples from each distribution, $\Theta(k/\varepsilon^2)$ samples are necessary and sufficient to learn $\textbf{p}_{\mathrm{avg}}$ to within error $\varepsilon$ in TV distance. To test uniformity or identity -- distinguishing the case that $\textbf{p}_{\mathrm{avg}}$ is equal to some reference distribution, versus has $\ell_1$ distance at least $\varepsilon$ from the reference distribution, we show that a linear number of samples in $k$ is necessary given $c=1$ samples from each distribution. In contrast, for $c \ge 2$, we recover the usual sublinear sample testing of the i.i.d. setting: we show that $O(\sqrt{k}/\varepsilon^2 + 1/\varepsilon^4)$ samples are sufficient, matching the optimal sample complexity in the i.i.d. case in the regime where $\varepsilon \ge k^{-1/4}$. Additionally, we show that in the $c=2$ case, there is a constant $\rho > 0$ such that even in the linear regime with $\rho k$ samples, no tester that considers the multiset of samples (ignoring which samples were drawn from the same $\textbf{p}_i$) can perform uniformity testing.

What Can Transformers Learn In-Context? A Case Study of Simple Function Classes

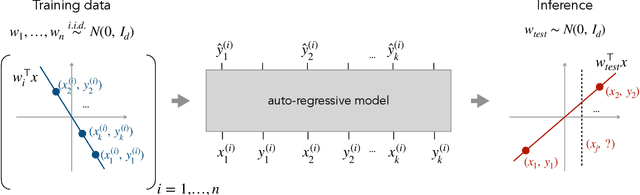
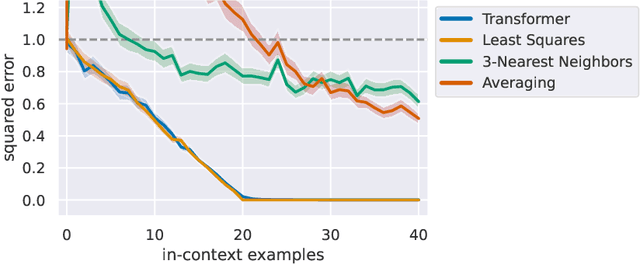
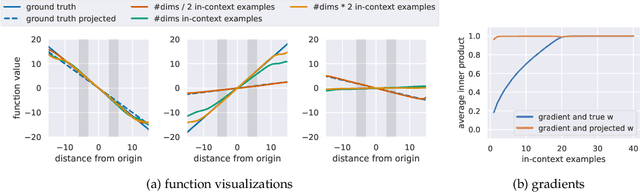
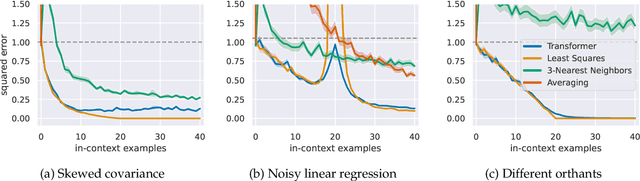
In-context learning refers to the ability of a model to condition on a prompt sequence consisting of in-context examples (input-output pairs corresponding to some task) along with a new query input, and generate the corresponding output. Crucially, in-context learning happens only at inference time without any parameter updates to the model. While large language models such as GPT-3 exhibit some ability to perform in-context learning, it is unclear what the relationship is between tasks on which this succeeds and what is present in the training data. To make progress towards understanding in-context learning, we consider the well-defined problem of training a model to in-context learn a function class (e.g., linear functions): that is, given data derived from some functions in the class, can we train a model to in-context learn "most" functions from this class? We show empirically that standard Transformers can be trained from scratch to perform in-context learning of linear functions -- that is, the trained model is able to learn unseen linear functions from in-context examples with performance comparable to the optimal least squares estimator. In fact, in-context learning is possible even under two forms of distribution shift: (i) between the training data of the model and inference-time prompts, and (ii) between the in-context examples and the query input during inference. We also show that we can train Transformers to in-context learn more complex function classes -- namely sparse linear functions, two-layer neural networks, and decision trees -- with performance that matches or exceeds task-specific learning algorithms. Our code and models are available at https://github.com/dtsip/in-context-learning .

Accurate Link Lifetime Computation in Autonomous Airborne UAV Networks

An autonomous airborne network (AN) consists of multiple unmanned aerial vehicles (UAVs), which can self-configure to provide seamless, low-cost and secure connectivity. AN is preferred for applications in civilian and military sectors because it can improve the network reliability and fault tolerance, reduce mission completion time through collaboration, and adapt to dynamic mission requirements. However, facilitating seamless communication in such ANs is a challenging task due to their fast node mobility, which results in frequent link disruptions. Many existing AN-specific mobility-aware schemes restrictively assume that UAVs fly in straight lines, to reduce the high uncertainty in the mobility pattern and simplify the calculation of link lifetime (LLT). Here, LLT represents the duration after which the link between a node pair terminates. However, the application of such schemes is severely limited, which makes them unsuitable for practical autonomous ANs. In this report, a mathematical framework is described to accurately compute the \textit{LLT} value for a UAV node pair, where each node flies independently in a randomly selected smooth trajectory. In addition, the impact of random trajectory changes on LLT accuracy is also discussed.

On the Statistical Complexity of Sample Amplification

Given $n$ i.i.d. samples drawn from an unknown distribution $P$, when is it possible to produce a larger set of $n+m$ samples which cannot be distinguished from $n+m$ i.i.d. samples drawn from $P$? (Axelrod et al. 2019) formalized this question as the sample amplification problem, and gave optimal amplification procedures for discrete distributions and Gaussian location models. However, these procedures and associated lower bounds are tailored to the specific distribution classes, and a general statistical understanding of sample amplification is still largely missing. In this work, we place the sample amplification problem on a firm statistical foundation by deriving generally applicable amplification procedures, lower bound techniques and connections to existing statistical notions. Our techniques apply to a large class of distributions including the exponential family, and establish a rigorous connection between sample amplification and distribution learning.