Efficient Swap Multicalibration of Elicitable Properties

Multicalibration [HJKRR18] is an algorithmic fairness perspective that demands that the predictions of a predictor are correct conditional on themselves and membership in a collection of potentially overlapping subgroups of a population. The work of [NR23] established a surprising connection between multicalibration for an arbitrary property $\Gamma$ (e.g., mean or median) and property elicitation: a property $\Gamma$ can be multicalibrated if and only if it is elicitable, where elicitability is the notion that the true property value of a distribution can be obtained by solving a regression problem over the distribution. In the online setting, [NR23] proposed an inefficient algorithm that achieves $\sqrt T$ $\ell_2$-multicalibration error for a hypothesis class of group membership functions and an elicitable property $\Gamma$, after $T$ rounds of interaction between a forecaster and adversary. In this paper, we generalize multicalibration for an elicitable property $\Gamma$ from group membership functions to arbitrary bounded hypothesis classes and introduce a stronger notion -- swap multicalibration, following [GKR23]. Subsequently, we propose an oracle-efficient algorithm which, when given access to an online agnostic learner, achieves $T^{1/(r+1)}$ $\ell_r$-swap multicalibration error with high probability (for $r\ge2$) for a hypothesis class with bounded sequential Rademacher complexity and an elicitable property $\Gamma$. For the special case of $r=2$, this implies an oracle-efficient algorithm that achieves $T^{1/3}$ $\ell_2$-swap multicalibration error, which significantly improves on the previously established bounds for the problem [NR23, GMS25, LSS25a], and completely resolves an open question raised in [GJRR24] on the possibility of an oracle-efficient algorithm that achieves $\sqrt{T}$ $\ell_2$-mean multicalibration error by answering it in a strongly affirmative sense.

How Muon's Spectral Design Benefits Generalization: A Study on Imbalanced Data

The growing adoption of spectrum-aware matrix-valued optimizers such as Muon and Shampoo in deep learning motivates a systematic study of their generalization properties and, in particular, when they might outperform competitive algorithms. We approach this question by introducing appropriate simplifying abstractions as follows: First, we use imbalanced data as a testbed. Second, we study the canonical form of such optimizers, which is Spectral Gradient Descent (SpecGD) -- each update step is $UV^T$ where $U\Sigma V^T$ is the truncated SVD of the gradient. Third, within this framework we identify a canonical setting for which we precisely quantify when SpecGD outperforms vanilla Euclidean GD. For a Gaussian mixture data model and both linear and bilinear models, we show that unlike GD, which prioritizes learning dominant principal components of the data first, SpecGD learns all principal components of the data at equal rates. We demonstrate how this translates to a growing gap in balanced accuracy favoring SpecGD early in training and further show that the gap remains consistent even when the GD counterpart uses adaptive step-sizes via normalization. By extending the analysis to deep linear models, we show that depth amplifies these effects. We empirically verify our theoretical findings on a variety of imbalanced datasets. Our experiments compare practical variants of spectral methods, like Muon and Shampoo, against their Euclidean counterparts and Adam. The results validate our findings that these spectral optimizers achieve superior generalization by promoting a more balanced learning of the data's underlying components.

Zebra-CoT: A Dataset for Interleaved Vision Language Reasoning

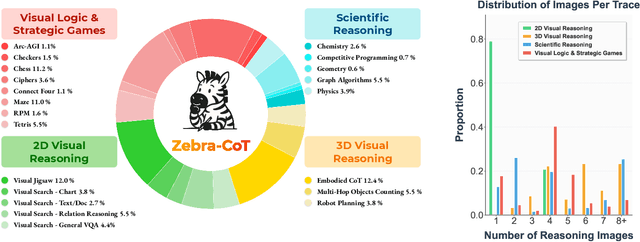
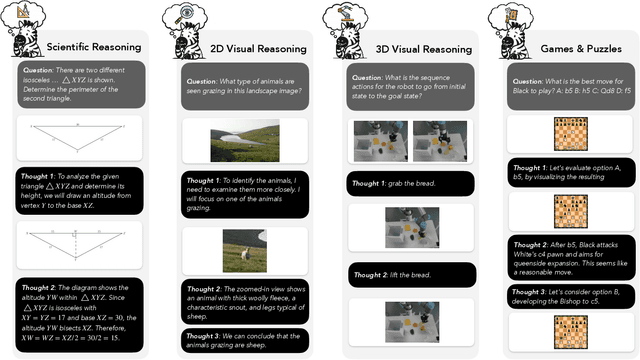
Humans often use visual aids, for example diagrams or sketches, when solving complex problems. Training multimodal models to do the same, known as Visual Chain of Thought (Visual CoT), is challenging due to: (1) poor off-the-shelf visual CoT performance, which hinders reinforcement learning, and (2) the lack of high-quality visual CoT training data. We introduce $\textbf{Zebra-CoT}$, a diverse large-scale dataset with 182,384 samples, containing logically coherent interleaved text-image reasoning traces. We focus on four categories of tasks where sketching or visual reasoning is especially natural, spanning scientific questions such as geometry, physics, and algorithms; 2D visual reasoning tasks like visual search and jigsaw puzzles; 3D reasoning tasks including 3D multi-hop inference, embodied and robot planning; visual logic problems and strategic games like chess. Fine-tuning the Anole-7B model on the Zebra-CoT training corpus results in an improvement of +12% in our test-set accuracy and yields up to +13% performance gain on standard VLM benchmark evaluations. Fine-tuning Bagel-7B yields a model that generates high-quality interleaved visual reasoning chains, underscoring Zebra-CoT's effectiveness for developing multimodal reasoning abilities. We open-source our dataset and models to support development and evaluation of visual CoT.

From Calibration to Collaboration: LLM Uncertainty Quantification Should Be More Human-Centered

Large Language Models (LLMs) are increasingly assisting users in the real world, yet their reliability remains a concern. Uncertainty quantification (UQ) has been heralded as a tool to enhance human-LLM collaboration by enabling users to know when to trust LLM predictions. We argue that current practices for uncertainty quantification in LLMs are not optimal for developing useful UQ for human users making decisions in real-world tasks. Through an analysis of 40 LLM UQ methods, we identify three prevalent practices hindering the community's progress toward its goal of benefiting downstream users: 1) evaluating on benchmarks with low ecological validity; 2) considering only epistemic uncertainty; and 3) optimizing metrics that are not necessarily indicative of downstream utility. For each issue, we propose concrete user-centric practices and research directions that LLM UQ researchers should consider. Instead of hill-climbing on unrepresentative tasks using imperfect metrics, we argue that the community should adopt a more human-centered approach to LLM uncertainty quantification.

The Rich and the Simple: On the Implicit Bias of Adam and SGD

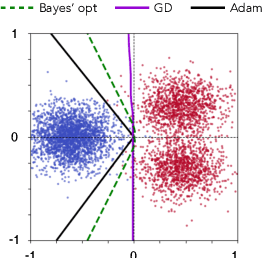
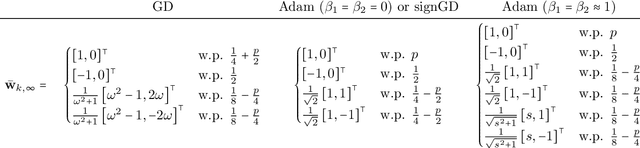
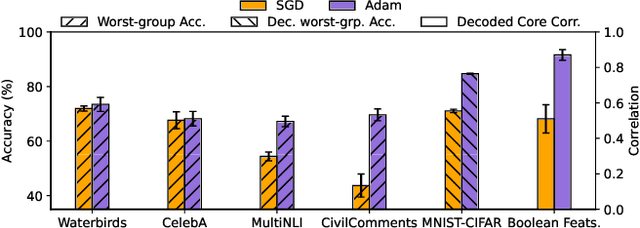
Adam is the de facto optimization algorithm for several deep learning applications, but an understanding of its implicit bias and how it differs from other algorithms, particularly standard first-order methods such as (stochastic) gradient descent (GD), remains limited. In practice, neural networks trained with SGD are known to exhibit simplicity bias -- a tendency to find simple solutions. In contrast, we show that Adam is more resistant to such simplicity bias. To demystify this phenomenon, in this paper, we investigate the differences in the implicit biases of Adam and GD when training two-layer ReLU neural networks on a binary classification task involving synthetic data with Gaussian clusters. We find that GD exhibits a simplicity bias, resulting in a linear decision boundary with a suboptimal margin, whereas Adam leads to much richer and more diverse features, producing a nonlinear boundary that is closer to the Bayes' optimal predictor. This richer decision boundary also allows Adam to achieve higher test accuracy both in-distribution and under certain distribution shifts. We theoretically prove these results by analyzing the population gradients. To corroborate our theoretical findings, we present empirical results showing that this property of Adam leads to superior generalization across datasets with spurious correlations where neural networks trained with SGD are known to show simplicity bias and don't generalize well under certain distributional shifts.

Improved Bounds for Swap Multicalibration and Swap Omniprediction

In this paper, we consider the related problems of multicalibration -- a multigroup fairness notion and omniprediction -- a simultaneous loss minimization paradigm, both in the distributional and online settings. The recent work of Garg et al. (2024) raised the open problem of whether it is possible to efficiently achieve $O(\sqrt{T})$ $\ell_{2}$-multicalibration error against bounded linear functions. In this paper, we answer this question in a strongly affirmative sense. We propose an efficient algorithm that achieves $O(T^{\frac{1}{3}})$ $\ell_{2}$-swap multicalibration error (both in high probability and expectation). On propagating this bound onward, we obtain significantly improved rates for $\ell_{1}$-swap multicalibration and swap omniprediction for a loss class of convex Lipschitz functions. In particular, we show that our algorithm achieves $O(T^{\frac{2}{3}})$ $\ell_{1}$-swap multicalibration and swap omniprediction errors, thereby improving upon the previous best-known bound of $O(T^{\frac{7}{8}})$. As a consequence of our improved online results, we further obtain several improved sample complexity rates in the distributional setting. In particular, we establish a $O(\varepsilon ^ {-3})$ sample complexity of efficiently learning an $\varepsilon$-swap omnipredictor for the class of convex and Lipschitz functions, $O(\varepsilon ^{-2.5})$ sample complexity of efficiently learning an $\varepsilon$-swap agnostic learner for the squared loss, and $O(\varepsilon ^ {-5}), O(\varepsilon ^ {-2.5})$ sample complexities of learning $\ell_{1}, \ell_{2}$-swap multicalibrated predictors against linear functions, all of which significantly improve on the previous best-known bounds.

Textual Steering Vectors Can Improve Visual Understanding in Multimodal Large Language Models

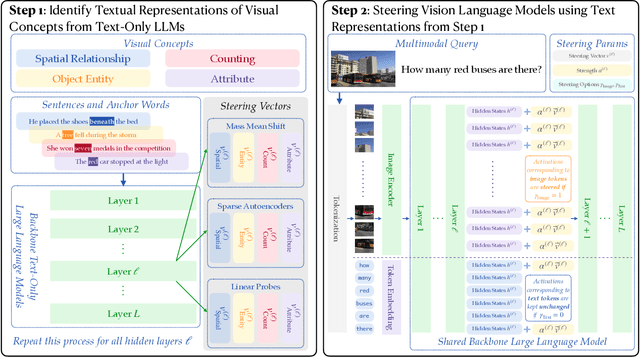
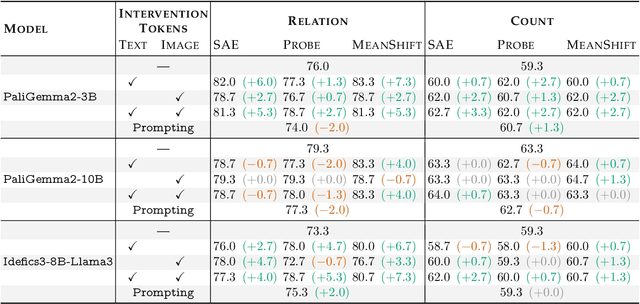
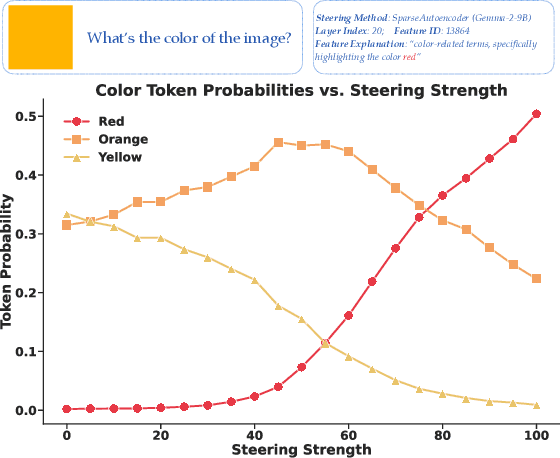
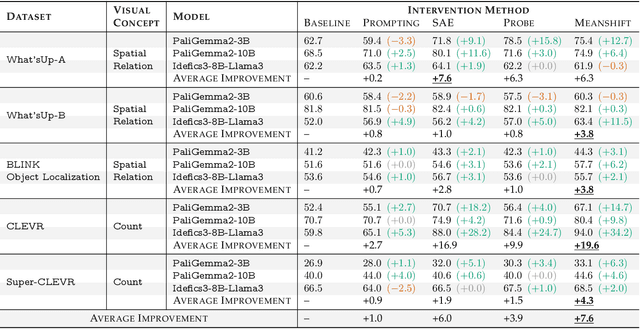
Steering methods have emerged as effective and targeted tools for guiding large language models' (LLMs) behavior without modifying their parameters. Multimodal large language models (MLLMs), however, do not currently enjoy the same suite of techniques, due in part to their recency and architectural diversity. Inspired by this gap, we investigate whether MLLMs can be steered using vectors derived from their text-only LLM backbone, via sparse autoencoders (SAEs), mean shift, and linear probing. We find that text-derived steering consistently enhances multimodal accuracy across diverse MLLM architectures and visual tasks. In particular, mean shift boosts spatial relationship accuracy on CV-Bench by up to +7.3% and counting accuracy by up to +3.3%, outperforming prompting and exhibiting strong generalization to out-of-distribution datasets. These results highlight textual steering vectors as a powerful, efficient mechanism for enhancing grounding in MLLMs with minimal additional data collection and computational overhead.

Simultaneous Swap Regret Minimization via KL-Calibration

Calibration is a fundamental concept that aims at ensuring the reliability of probabilistic predictions by aligning them with real-world outcomes. There is a surge of studies on new calibration measures that are easier to optimize compared to the classical $\ell_1$-Calibration while still having strong implications for downstream applications. One recent such example is the work by Fishelson et al. (2025) who show that it is possible to achieve $O(T^{1/3})$ pseudo $\ell_2$-Calibration error via minimizing pseudo swap regret of the squared loss, which in fact implies the same bound for all bounded proper losses with a smooth univariate form. In this work, we significantly generalize their result in the following ways: (a) in addition to smooth univariate forms, our algorithm also simultaneously achieves $O(T^{1/3})$ swap regret for any proper loss with a twice continuously differentiable univariate form (such as Tsallis entropy); (b) our bounds hold not only for pseudo swap regret that measures losses using the forecaster's distributions on predictions, but also hold for the actual swap regret that measures losses using the forecaster's actual realized predictions. We achieve so by introducing a new stronger notion of calibration called (pseudo) KL-Calibration, which we show is equivalent to the (pseudo) swap regret for log loss. We prove that there exists an algorithm that achieves $O(T^{1/3})$ KL-Calibration error and provide an explicit algorithm that achieves $O(T^{1/3})$ pseudo KL-Calibration error. Moreover, we show that the same algorithm achieves $O(T^{1/3}(\log T)^{-1/3}\log(T/\delta))$ swap regret w.p. $\ge 1-\delta$ for any proper loss with a smooth univariate form, which implies $O(T^{1/3})$ $\ell_2$-Calibration error. A technical contribution of our work is a new randomized rounding procedure and a non-uniform discretization scheme to minimize the swap regret for log loss.

Discovering Data Structures: Nearest Neighbor Search and Beyond

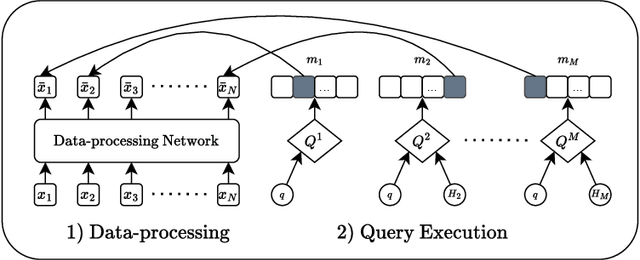
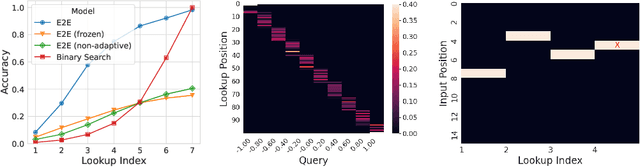
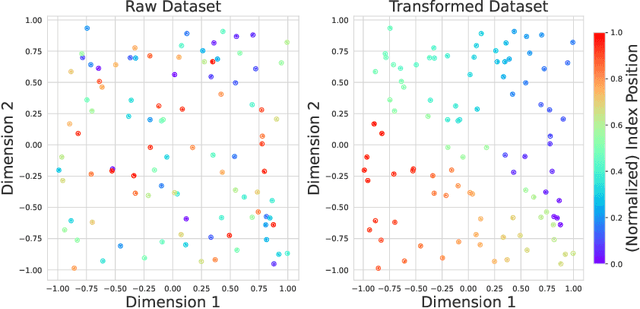
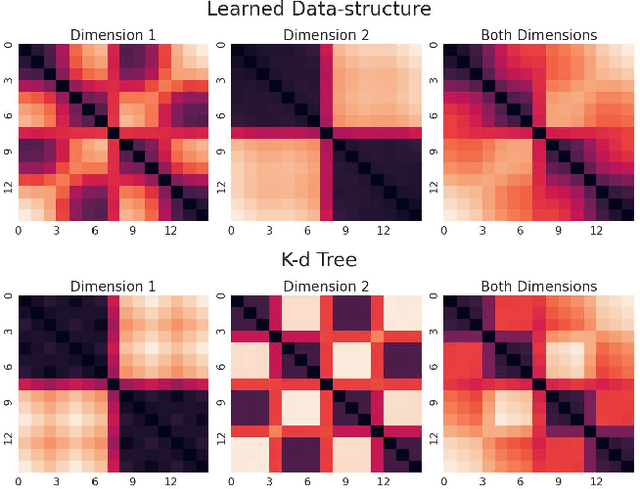
We propose a general framework for end-to-end learning of data structures. Our framework adapts to the underlying data distribution and provides fine-grained control over query and space complexity. Crucially, the data structure is learned from scratch, and does not require careful initialization or seeding with candidate data structures/algorithms. We first apply this framework to the problem of nearest neighbor search. In several settings, we are able to reverse-engineer the learned data structures and query algorithms. For 1D nearest neighbor search, the model discovers optimal distribution (in)dependent algorithms such as binary search and variants of interpolation search. In higher dimensions, the model learns solutions that resemble k-d trees in some regimes, while in others, they have elements of locality-sensitive hashing. The model can also learn useful representations of high-dimensional data and exploit them to design effective data structures. We also adapt our framework to the problem of estimating frequencies over a data stream, and believe it could also be a powerful discovery tool for new problems.

When is Multicalibration Post-Processing Necessary?

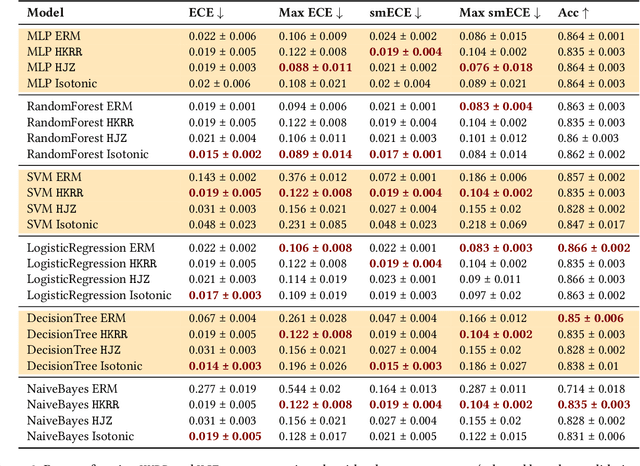
Calibration is a well-studied property of predictors which guarantees meaningful uncertainty estimates. Multicalibration is a related notion -- originating in algorithmic fairness -- which requires predictors to be simultaneously calibrated over a potentially complex and overlapping collection of protected subpopulations (such as groups defined by ethnicity, race, or income). We conduct the first comprehensive study evaluating the usefulness of multicalibration post-processing across a broad set of tabular, image, and language datasets for models spanning from simple decision trees to 90 million parameter fine-tuned LLMs. Our findings can be summarized as follows: (1) models which are calibrated out of the box tend to be relatively multicalibrated without any additional post-processing; (2) multicalibration post-processing can help inherently uncalibrated models; and (3) traditional calibration measures may sometimes provide multicalibration implicitly. More generally, we also distill many independent observations which may be useful for practical and effective applications of multicalibration post-processing in real-world contexts.