Pre-trained Large Language Models Use Fourier Features to Compute Addition
Paper and Code
Jun 05, 2024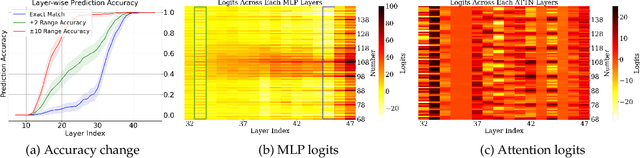

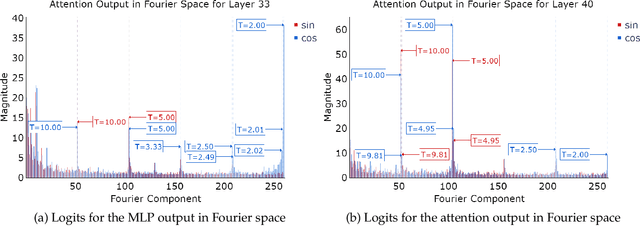
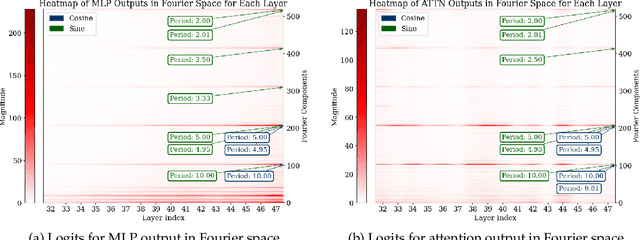
Pre-trained large language models (LLMs) exhibit impressive mathematical reasoning capabilities, yet how they compute basic arithmetic, such as addition, remains unclear. This paper shows that pre-trained LLMs add numbers using Fourier features -- dimensions in the hidden state that represent numbers via a set of features sparse in the frequency domain. Within the model, MLP and attention layers use Fourier features in complementary ways: MLP layers primarily approximate the magnitude of the answer using low-frequency features, while attention layers primarily perform modular addition (e.g., computing whether the answer is even or odd) using high-frequency features. Pre-training is crucial for this mechanism: models trained from scratch to add numbers only exploit low-frequency features, leading to lower accuracy. Introducing pre-trained token embeddings to a randomly initialized model rescues its performance. Overall, our analysis demonstrates that appropriate pre-trained representations (e.g., Fourier features) can unlock the ability of Transformers to learn precise mechanisms for algorithmic tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge