Full-Batch Gradient Descent Outperforms One-Pass SGD: Sample Complexity Separation in Single-Index Learning

It is folklore that reusing training data more than once can improve the statistical efficiency of gradient-based learning. However, beyond linear regression, the theoretical advantage of full-batch gradient descent (GD, which always reuses all the data) over one-pass stochastic gradient descent (online SGD, which uses each data point only once) remains unclear. In this work, we consider learning a $d$-dimensional single-index model with a quadratic activation, for which it is known that one-pass SGD requires $n\gtrsim d\log d$ samples to achieve weak recovery. We first show that this $\log d$ factor in the sample complexity persists for full-batch spherical GD on the correlation loss; however, by simply truncating the activation, full-batch GD exhibits a favorable optimization landscape at $n \simeq d$ samples, thereby outperforming one-pass SGD (with the same activation) in statistical efficiency. We complement this result with a trajectory analysis of full-batch GD on the squared loss from small initialization, showing that $n \gtrsim d$ samples and $T \gtrsim\log d$ gradient steps suffice to achieve strong (exact) recovery.

Hyperphantasia: A Benchmark for Evaluating the Mental Visualization Capabilities of Multimodal LLMs

Mental visualization, the ability to construct and manipulate visual representations internally, is a core component of human cognition and plays a vital role in tasks involving reasoning, prediction, and abstraction. Despite the rapid progress of Multimodal Large Language Models (MLLMs), current benchmarks primarily assess passive visual perception, offering limited insight into the more active capability of internally constructing visual patterns to support problem solving. Yet mental visualization is a critical cognitive skill in humans, supporting abilities such as spatial navigation, predicting physical trajectories, and solving complex visual problems through imaginative simulation. To bridge this gap, we introduce Hyperphantasia, a synthetic benchmark designed to evaluate the mental visualization abilities of MLLMs through four carefully constructed puzzles. Each task is procedurally generated and presented at three difficulty levels, enabling controlled analysis of model performance across increasing complexity. Our comprehensive evaluation of state-of-the-art models reveals a substantial gap between the performance of humans and MLLMs. Additionally, we explore the potential of reinforcement learning to improve visual simulation capabilities. Our findings suggest that while some models exhibit partial competence in recognizing visual patterns, robust mental visualization remains an open challenge for current MLLMs.

The Rich and the Simple: On the Implicit Bias of Adam and SGD

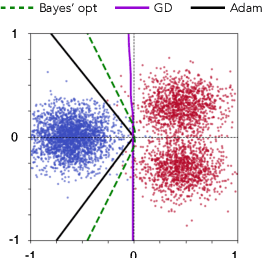
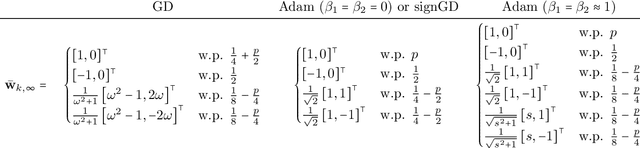
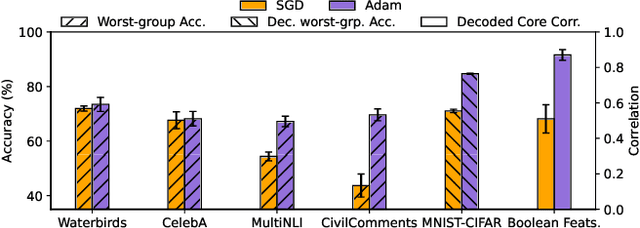
Adam is the de facto optimization algorithm for several deep learning applications, but an understanding of its implicit bias and how it differs from other algorithms, particularly standard first-order methods such as (stochastic) gradient descent (GD), remains limited. In practice, neural networks trained with SGD are known to exhibit simplicity bias -- a tendency to find simple solutions. In contrast, we show that Adam is more resistant to such simplicity bias. To demystify this phenomenon, in this paper, we investigate the differences in the implicit biases of Adam and GD when training two-layer ReLU neural networks on a binary classification task involving synthetic data with Gaussian clusters. We find that GD exhibits a simplicity bias, resulting in a linear decision boundary with a suboptimal margin, whereas Adam leads to much richer and more diverse features, producing a nonlinear boundary that is closer to the Bayes' optimal predictor. This richer decision boundary also allows Adam to achieve higher test accuracy both in-distribution and under certain distribution shifts. We theoretically prove these results by analyzing the population gradients. To corroborate our theoretical findings, we present empirical results showing that this property of Adam leads to superior generalization across datasets with spurious correlations where neural networks trained with SGD are known to show simplicity bias and don't generalize well under certain distributional shifts.

Emergence and Evolution of Interpretable Concepts in Diffusion Models

Diffusion models have become the go-to method for text-to-image generation, producing high-quality images from noise through a process called reverse diffusion. Understanding the dynamics of the reverse diffusion process is crucial in steering the generation and achieving high sample quality. However, the inner workings of diffusion models is still largely a mystery due to their black-box nature and complex, multi-step generation process. Mechanistic Interpretability (MI) techniques, such as Sparse Autoencoders (SAEs), aim at uncovering the operating principles of models through granular analysis of their internal representations. These MI techniques have been successful in understanding and steering the behavior of large language models at scale. However, the great potential of SAEs has not yet been applied toward gaining insight into the intricate generative process of diffusion models. In this work, we leverage the SAE framework to probe the inner workings of a popular text-to-image diffusion model, and uncover a variety of human-interpretable concepts in its activations. Interestingly, we find that even before the first reverse diffusion step is completed, the final composition of the scene can be predicted surprisingly well by looking at the spatial distribution of activated concepts. Moreover, going beyond correlational analysis, we show that the discovered concepts have a causal effect on the model output and can be leveraged to steer the generative process. We design intervention techniques aimed at manipulating image composition and style, and demonstrate that (1) in early stages of diffusion image composition can be effectively controlled, (2) in the middle stages of diffusion image composition is finalized, however stylistic interventions are effective, and (3) in the final stages of diffusion only minor textural details are subject to change.

Test-Time Training Provably Improves Transformers as In-context Learners

Test-time training (TTT) methods explicitly update the weights of a model to adapt to the specific test instance, and they have found success in a variety of settings, including most recently language modeling and reasoning. To demystify this success, we investigate a gradient-based TTT algorithm for in-context learning, where we train a transformer model on the in-context demonstrations provided in the test prompt. Specifically, we provide a comprehensive theoretical characterization of linear transformers when the update rule is a single gradient step. Our theory (i) delineates the role of alignment between pretraining distribution and target task, (ii) demystifies how TTT can alleviate distribution shift, and (iii) quantifies the sample complexity of TTT including how it can significantly reduce the eventual sample size required for in-context learning. As our empirical contribution, we study the benefits of TTT for TabPFN, a tabular foundation model. In line with our theory, we demonstrate that TTT significantly reduces the required sample size for tabular classification (3 to 5 times fewer) unlocking substantial inference efficiency with a negligible training cost.

CryptoMamba: Leveraging State Space Models for Accurate Bitcoin Price Prediction

Predicting Bitcoin price remains a challenging problem due to the high volatility and complex non-linear dynamics of cryptocurrency markets. Traditional time-series models, such as ARIMA and GARCH, and recurrent neural networks, like LSTMs, have been widely applied to this task but struggle to capture the regime shifts and long-range dependencies inherent in the data. In this work, we propose CryptoMamba, a novel Mamba-based State Space Model (SSM) architecture designed to effectively capture long-range dependencies in financial time-series data. Our experiments show that CryptoMamba not only provides more accurate predictions but also offers enhanced generalizability across different market conditions, surpassing the limitations of previous models. Coupled with trading algorithms for real-world scenarios, CryptoMamba demonstrates its practical utility by translating accurate forecasts into financial outcomes. Our findings signal a huge advantage for SSMs in stock and cryptocurrency price forecasting tasks.

Stability properties of gradient flow dynamics for the symmetric low-rank matrix factorization problem

The symmetric low-rank matrix factorization serves as a building block in many learning tasks, including matrix recovery and training of neural networks. However, despite a flurry of recent research, the dynamics of its training via non-convex factorized gradient-descent-type methods is not fully understood especially in the over-parameterized regime where the fitted rank is higher than the true rank of the target matrix. To overcome this challenge, we characterize equilibrium points of the gradient flow dynamics and examine their local and global stability properties. To facilitate a precise global analysis, we introduce a nonlinear change of variables that brings the dynamics into a cascade connection of three subsystems whose structure is simpler than the structure of the original system. We demonstrate that the Schur complement to a principal eigenspace of the target matrix is governed by an autonomous system that is decoupled from the rest of the dynamics. In the over-parameterized regime, we show that this Schur complement vanishes at an $O(1/t)$ rate, thereby capturing the slow dynamics that arises from excess parameters. We utilize a Lyapunov-based approach to establish exponential convergence of the other two subsystems. By decoupling the fast and slow parts of the dynamics, we offer new insight into the shape of the trajectories associated with local search algorithms and provide a complete characterization of the equilibrium points and their global stability properties. Such an analysis via nonlinear control techniques may prove useful in several related over-parameterized problems.

Theoretical Insights into Overparameterized Models in Multi-Task and Replay-Based Continual Learning

Multi-task learning (MTL) is a machine learning paradigm that aims to improve the generalization performance of a model on multiple related tasks by training it simultaneously on those tasks. Unlike MTL, where the model has instant access to the training data of all tasks, continual learning (CL) involves adapting to new sequentially arriving tasks over time without forgetting the previously acquired knowledge. Despite the wide practical adoption of CL and MTL and extensive literature on both areas, there remains a gap in the theoretical understanding of these methods when used with overparameterized models such as deep neural networks. This paper studies the overparameterized linear models as a proxy for more complex models. We develop theoretical results describing the effect of various system parameters on the model's performance in an MTL setup. Specifically, we study the impact of model size, dataset size, and task similarity on the generalization error and knowledge transfer. Additionally, we present theoretical results to characterize the performance of replay-based CL models. Our results reveal the impact of buffer size and model capacity on the forgetting rate in a CL setup and help shed light on some of the state-of-the-art CL methods. Finally, through extensive empirical evaluations, we demonstrate that our theoretical findings are also applicable to deep neural networks, offering valuable guidance for designing MTL and CL models in practice.

Serpent: Scalable and Efficient Image Restoration via Multi-scale Structured State Space Models

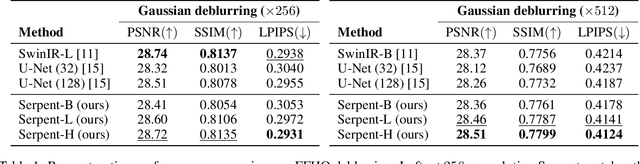
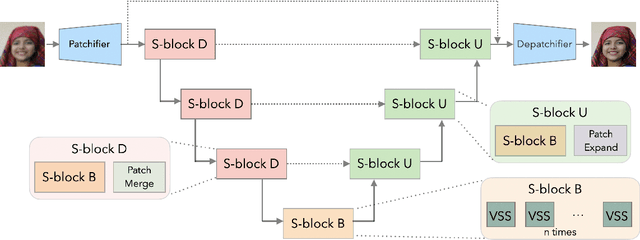
The landscape of computational building blocks of efficient image restoration architectures is dominated by a combination of convolutional processing and various attention mechanisms. However, convolutional filters are inherently local and therefore struggle at modeling long-range dependencies in images. On the other hand, attention excels at capturing global interactions between arbitrary image regions, however at a quadratic cost in image dimension. In this work, we propose Serpent, an architecture that leverages recent advances in state space models (SSMs) in its core computational block. SSMs, originally introduced for sequence modeling, can maintain a global receptive field with a favorable linear scaling in input size. Our preliminary results demonstrate that Serpent can achieve reconstruction quality on par with state-of-the-art techniques, while requiring orders of magnitude less compute (up to $150$ fold reduction in FLOPS) and a factor of up to $5\times$ less GPU memory while maintaining a compact model size.

A Data-Free Approach to Mitigate Catastrophic Forgetting in Federated Class Incremental Learning for Vision Tasks

Deep learning models often suffer from forgetting previously learned information when trained on new data. This problem is exacerbated in federated learning (FL), where the data is distributed and can change independently for each user. Many solutions are proposed to resolve this catastrophic forgetting in a centralized setting. However, they do not apply directly to FL because of its unique complexities, such as privacy concerns and resource limitations. To overcome these challenges, this paper presents a framework for $\textbf{federated class incremental learning}$ that utilizes a generative model to synthesize samples from past distributions. This data can be later exploited alongside the training data to mitigate catastrophic forgetting. To preserve privacy, the generative model is trained on the server using data-free methods at the end of each task without requesting data from clients. Moreover, our solution does not demand the users to store old data or models, which gives them the freedom to join/leave the training at any time. Additionally, we introduce SuperImageNet, a new regrouping of the ImageNet dataset specifically tailored for federated continual learning. We demonstrate significant improvements compared to existing baselines through extensive experiments on multiple datasets.