Richard Leahy
Informed Bootstrap Augmentation Improves EEG Decoding
Nov 15, 2025Abstract:Electroencephalography (EEG) offers detailed access to neural dynamics but remains constrained by noise and trial-by-trial variability, limiting decoding performance in data-restricted or complex paradigms. Data augmentation is often employed to enhance feature representations, yet conventional uniform averaging overlooks differences in trial informativeness and can degrade representational quality. We introduce a weighted bootstrapping approach that prioritizes more reliable trials to generate higher-quality augmented samples. In a Sentence Evaluation paradigm, weights were computed from relative ERP differences and applied during probabilistic sampling and averaging. Across conditions, weighted bootstrapping improved decoding accuracy relative to unweighted (from 68.35% to 71.25% at best), demonstrating that emphasizing reliable trials strengthens representational quality. The results demonstrate that reliability-based augmentation yields more robust and discriminative EEG representations. The code is publicly available at https://github.com/lyricists/NeuroBootstrap.
Learning A Disentangling Representation For PU Learning
Oct 05, 2023Abstract:In this paper, we address the problem of learning a binary (positive vs. negative) classifier given Positive and Unlabeled data commonly referred to as PU learning. Although rudimentary techniques like clustering, out-of-distribution detection, or positive density estimation can be used to solve the problem in low-dimensional settings, their efficacy progressively deteriorates with higher dimensions due to the increasing complexities in the data distribution. In this paper we propose to learn a neural network-based data representation using a loss function that can be used to project the unlabeled data into two (positive and negative) clusters that can be easily identified using simple clustering techniques, effectively emulating the phenomenon observed in low-dimensional settings. We adopt a vector quantization technique for the learned representations to amplify the separation between the learned unlabeled data clusters. We conduct experiments on simulated PU data that demonstrate the improved performance of our proposed method compared to the current state-of-the-art approaches. We also provide some theoretical justification for our two cluster-based approach and our algorithmic choices.
Beta quantile regression for robust estimation of uncertainty in the presence of outliers
Sep 14, 2023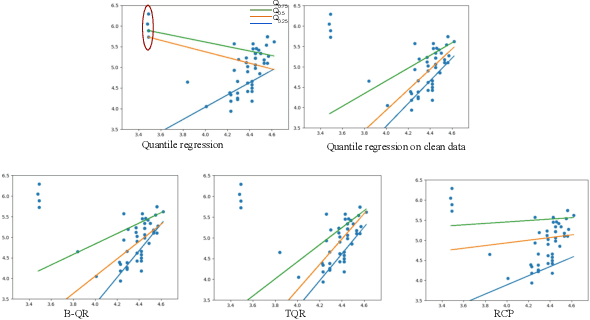
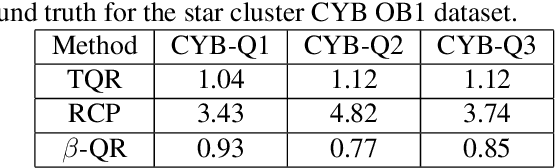
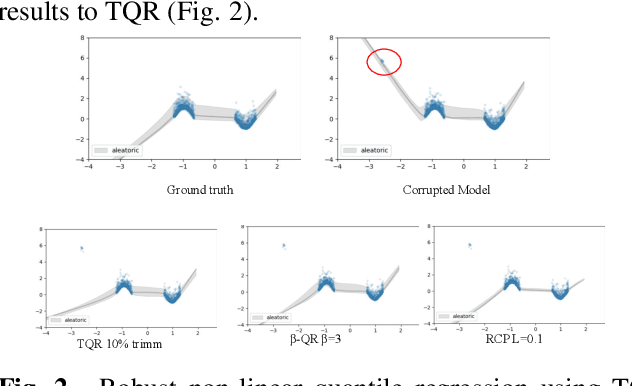
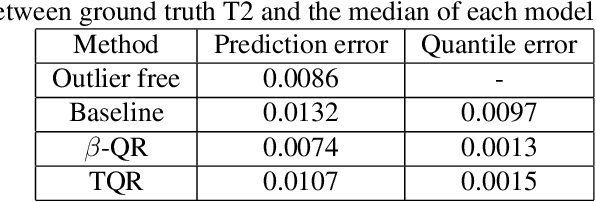
Abstract:Quantile Regression (QR) can be used to estimate aleatoric uncertainty in deep neural networks and can generate prediction intervals. Quantifying uncertainty is particularly important in critical applications such as clinical diagnosis, where a realistic assessment of uncertainty is essential in determining disease status and planning the appropriate treatment. The most common application of quantile regression models is in cases where the parametric likelihood cannot be specified. Although quantile regression is quite robust to outlier response observations, it can be sensitive to outlier covariate observations (features). Outlier features can compromise the performance of deep learning regression problems such as style translation, image reconstruction, and deep anomaly detection, potentially leading to misleading conclusions. To address this problem, we propose a robust solution for quantile regression that incorporates concepts from robust divergence. We compare the performance of our proposed method with (i) least trimmed quantile regression and (ii) robust regression based on the regularization of case-specific parameters in a simple real dataset in the presence of outlier. These methods have not been applied in a deep learning framework. We also demonstrate the applicability of the proposed method by applying it to a medical imaging translation task using diffusion models.
Learning From Positive and Unlabeled Data Using Observer-GAN
Aug 26, 2022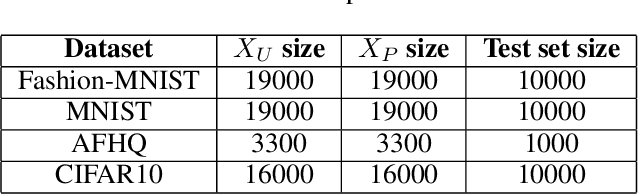



Abstract:The problem of learning from positive and unlabeled data (A.K.A. PU learning) has been studied in a binary (i.e., positive versus negative) classification setting, where the input data consist of (1) observations from the positive class and their corresponding labels, (2) unlabeled observations from both positive and negative classes. Generative Adversarial Networks (GANs) have been used to reduce the problem to the supervised setting with the advantage that supervised learning has state-of-the-art accuracy in classification tasks. In order to generate \textit{pseudo}-negative observations, GANs are trained on positive and unlabeled observations with a modified loss. Using both positive and \textit{pseudo}-negative observations leads to a supervised learning setting. The generation of pseudo-negative observations that are realistic enough to replace missing negative class samples is a bottleneck for current GAN-based algorithms. By including an additional classifier into the GAN architecture, we provide a novel GAN-based approach. In our suggested method, the GAN discriminator instructs the generator only to produce samples that fall into the unlabeled data distribution, while a second classifier (observer) network monitors the GAN training to: (i) prevent the generated samples from falling into the positive distribution; and (ii) learn the features that are the key distinction between the positive and negative observations. Experiments on four image datasets demonstrate that our trained observer network performs better than existing techniques in discriminating between real unseen positive and negative samples.
Deep Quantile Regression for Uncertainty Estimation in Unsupervised and Supervised Lesion Detection
Sep 20, 2021



Abstract:Despite impressive state-of-the-art performance on a wide variety of machine learning tasks in multiple applications, deep learning methods can produce over-confident predictions, particularly with limited training data. Therefore, quantifying uncertainty is particularly important in critical applications such as anomaly or lesion detection and clinical diagnosis, where a realistic assessment of uncertainty is essential in determining surgical margins, disease status and appropriate treatment. In this work, we focus on using quantile regression to estimate aleatoric uncertainty and use it for estimating uncertainty in both supervised and unsupervised lesion detection problems. In the unsupervised settings, we apply quantile regression to a lesion detection task using Variational AutoEncoder (VAE). The VAE models the output as a conditionally independent Gaussian characterized by means and variances for each output dimension. Unfortunately, joint optimization of both mean and variance in the VAE leads to the well-known problem of shrinkage or underestimation of variance. We describe an alternative VAE model, Quantile-Regression VAE (QR-VAE), that avoids this variance shrinkage problem by estimating conditional quantiles for the given input image. Using the estimated quantiles, we compute the conditional mean and variance for input images under the conditionally Gaussian model. We then compute reconstruction probability using this model as a principled approach to outlier or anomaly detection applications. In the supervised setting, we develop binary quantile regression (BQR) for the supervised lesion segmentation task. BQR segmentation can capture uncertainty in label boundaries. We show how quantile regression can be used to characterize expert disagreement in the location of lesion boundaries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge