PixelShuffler: A Simple Image Translation Through Pixel Rearrangement

Image-to-image translation is a topic in computer vision that has a vast range of use cases ranging from medical image translation, such as converting MRI scans to CT scans or to other MRI contrasts, to image colorization, super-resolution, domain adaptation, and generating photorealistic images from sketches or semantic maps. Image style transfer is also a widely researched application of image-to-image translation, where the goal is to synthesize an image that combines the content of one image with the style of another. Existing state-of-the-art methods often rely on complex neural networks, including diffusion models and language models, to achieve high-quality style transfer, but these methods can be computationally expensive and intricate to implement. In this paper, we propose a novel pixel shuffle method that addresses the image-to-image translation problem generally with a specific demonstrative application in style transfer. The proposed method approaches style transfer by shuffling the pixels of the style image such that the mutual information between the shuffled image and the content image is maximized. This approach inherently preserves the colors of the style image while ensuring that the structural details of the content image are retained in the stylized output. We demonstrate that this simple and straightforward method produces results that are comparable to state-of-the-art techniques, as measured by the Learned Perceptual Image Patch Similarity (LPIPS) loss for content preservation and the Fr\'echet Inception Distance (FID) score for style similarity. Our experiments validate that the proposed pixel shuffle method achieves competitive performance with significantly reduced complexity, offering a promising alternative for efficient image style transfer, as well as a promise in usability of the method in general image-to-image translation tasks.

Learning A Disentangling Representation For PU Learning

In this paper, we address the problem of learning a binary (positive vs. negative) classifier given Positive and Unlabeled data commonly referred to as PU learning. Although rudimentary techniques like clustering, out-of-distribution detection, or positive density estimation can be used to solve the problem in low-dimensional settings, their efficacy progressively deteriorates with higher dimensions due to the increasing complexities in the data distribution. In this paper we propose to learn a neural network-based data representation using a loss function that can be used to project the unlabeled data into two (positive and negative) clusters that can be easily identified using simple clustering techniques, effectively emulating the phenomenon observed in low-dimensional settings. We adopt a vector quantization technique for the learned representations to amplify the separation between the learned unlabeled data clusters. We conduct experiments on simulated PU data that demonstrate the improved performance of our proposed method compared to the current state-of-the-art approaches. We also provide some theoretical justification for our two cluster-based approach and our algorithmic choices.

Beta quantile regression for robust estimation of uncertainty in the presence of outliers

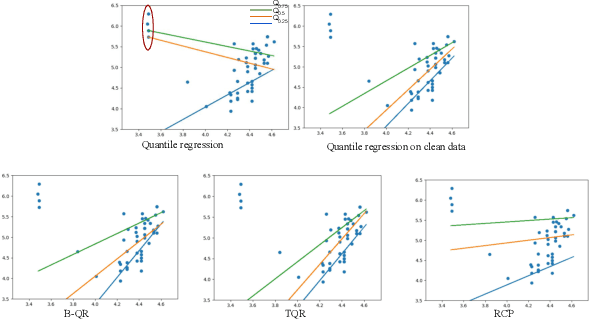
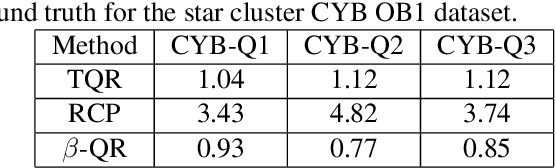
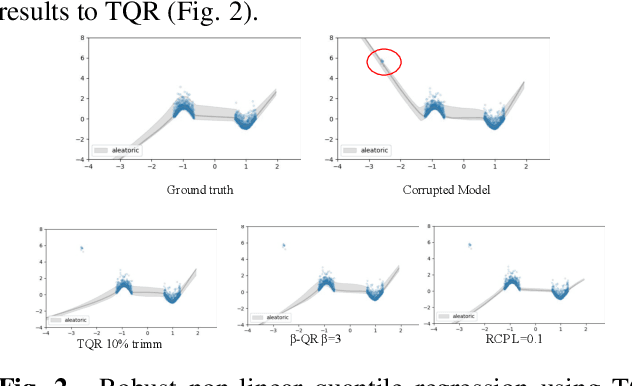
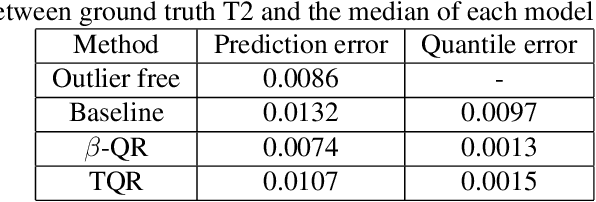
Quantile Regression (QR) can be used to estimate aleatoric uncertainty in deep neural networks and can generate prediction intervals. Quantifying uncertainty is particularly important in critical applications such as clinical diagnosis, where a realistic assessment of uncertainty is essential in determining disease status and planning the appropriate treatment. The most common application of quantile regression models is in cases where the parametric likelihood cannot be specified. Although quantile regression is quite robust to outlier response observations, it can be sensitive to outlier covariate observations (features). Outlier features can compromise the performance of deep learning regression problems such as style translation, image reconstruction, and deep anomaly detection, potentially leading to misleading conclusions. To address this problem, we propose a robust solution for quantile regression that incorporates concepts from robust divergence. We compare the performance of our proposed method with (i) least trimmed quantile regression and (ii) robust regression based on the regularization of case-specific parameters in a simple real dataset in the presence of outlier. These methods have not been applied in a deep learning framework. We also demonstrate the applicability of the proposed method by applying it to a medical imaging translation task using diffusion models.

Learning From Positive and Unlabeled Data Using Observer-GAN

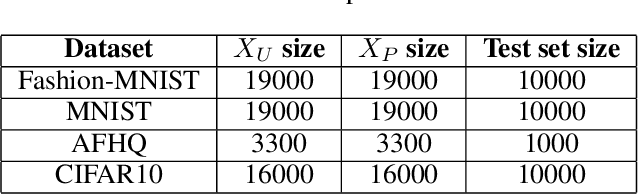
The problem of learning from positive and unlabeled data (A.K.A. PU learning) has been studied in a binary (i.e., positive versus negative) classification setting, where the input data consist of (1) observations from the positive class and their corresponding labels, (2) unlabeled observations from both positive and negative classes. Generative Adversarial Networks (GANs) have been used to reduce the problem to the supervised setting with the advantage that supervised learning has state-of-the-art accuracy in classification tasks. In order to generate \textit{pseudo}-negative observations, GANs are trained on positive and unlabeled observations with a modified loss. Using both positive and \textit{pseudo}-negative observations leads to a supervised learning setting. The generation of pseudo-negative observations that are realistic enough to replace missing negative class samples is a bottleneck for current GAN-based algorithms. By including an additional classifier into the GAN architecture, we provide a novel GAN-based approach. In our suggested method, the GAN discriminator instructs the generator only to produce samples that fall into the unlabeled data distribution, while a second classifier (observer) network monitors the GAN training to: (i) prevent the generated samples from falling into the positive distribution; and (ii) learn the features that are the key distinction between the positive and negative observations. Experiments on four image datasets demonstrate that our trained observer network performs better than existing techniques in discriminating between real unseen positive and negative samples.