Anand Joshi
Beta quantile regression for robust estimation of uncertainty in the presence of outliers
Sep 14, 2023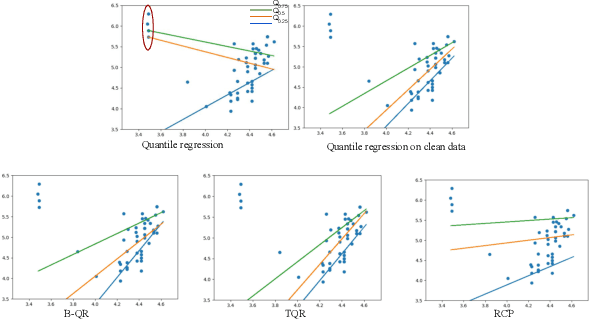
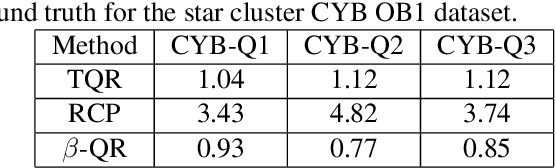
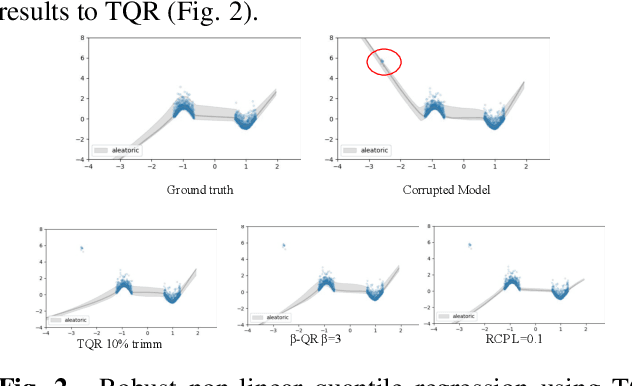
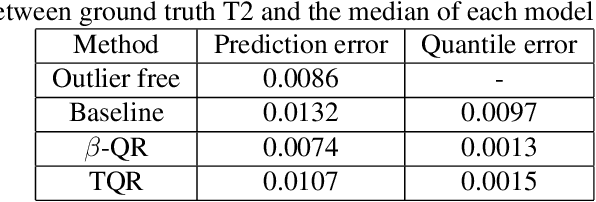
Abstract:Quantile Regression (QR) can be used to estimate aleatoric uncertainty in deep neural networks and can generate prediction intervals. Quantifying uncertainty is particularly important in critical applications such as clinical diagnosis, where a realistic assessment of uncertainty is essential in determining disease status and planning the appropriate treatment. The most common application of quantile regression models is in cases where the parametric likelihood cannot be specified. Although quantile regression is quite robust to outlier response observations, it can be sensitive to outlier covariate observations (features). Outlier features can compromise the performance of deep learning regression problems such as style translation, image reconstruction, and deep anomaly detection, potentially leading to misleading conclusions. To address this problem, we propose a robust solution for quantile regression that incorporates concepts from robust divergence. We compare the performance of our proposed method with (i) least trimmed quantile regression and (ii) robust regression based on the regularization of case-specific parameters in a simple real dataset in the presence of outlier. These methods have not been applied in a deep learning framework. We also demonstrate the applicability of the proposed method by applying it to a medical imaging translation task using diffusion models.
Deep Quantile Regression for Uncertainty Estimation in Unsupervised and Supervised Lesion Detection
Sep 20, 2021



Abstract:Despite impressive state-of-the-art performance on a wide variety of machine learning tasks in multiple applications, deep learning methods can produce over-confident predictions, particularly with limited training data. Therefore, quantifying uncertainty is particularly important in critical applications such as anomaly or lesion detection and clinical diagnosis, where a realistic assessment of uncertainty is essential in determining surgical margins, disease status and appropriate treatment. In this work, we focus on using quantile regression to estimate aleatoric uncertainty and use it for estimating uncertainty in both supervised and unsupervised lesion detection problems. In the unsupervised settings, we apply quantile regression to a lesion detection task using Variational AutoEncoder (VAE). The VAE models the output as a conditionally independent Gaussian characterized by means and variances for each output dimension. Unfortunately, joint optimization of both mean and variance in the VAE leads to the well-known problem of shrinkage or underestimation of variance. We describe an alternative VAE model, Quantile-Regression VAE (QR-VAE), that avoids this variance shrinkage problem by estimating conditional quantiles for the given input image. Using the estimated quantiles, we compute the conditional mean and variance for input images under the conditionally Gaussian model. We then compute reconstruction probability using this model as a principled approach to outlier or anomaly detection applications. In the supervised setting, we develop binary quantile regression (BQR) for the supervised lesion segmentation task. BQR segmentation can capture uncertainty in label boundaries. We show how quantile regression can be used to characterize expert disagreement in the location of lesion boundaries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge