Stability properties of gradient flow dynamics for the symmetric low-rank matrix factorization problem

The symmetric low-rank matrix factorization serves as a building block in many learning tasks, including matrix recovery and training of neural networks. However, despite a flurry of recent research, the dynamics of its training via non-convex factorized gradient-descent-type methods is not fully understood especially in the over-parameterized regime where the fitted rank is higher than the true rank of the target matrix. To overcome this challenge, we characterize equilibrium points of the gradient flow dynamics and examine their local and global stability properties. To facilitate a precise global analysis, we introduce a nonlinear change of variables that brings the dynamics into a cascade connection of three subsystems whose structure is simpler than the structure of the original system. We demonstrate that the Schur complement to a principal eigenspace of the target matrix is governed by an autonomous system that is decoupled from the rest of the dynamics. In the over-parameterized regime, we show that this Schur complement vanishes at an $O(1/t)$ rate, thereby capturing the slow dynamics that arises from excess parameters. We utilize a Lyapunov-based approach to establish exponential convergence of the other two subsystems. By decoupling the fast and slow parts of the dynamics, we offer new insight into the shape of the trajectories associated with local search algorithms and provide a complete characterization of the equilibrium points and their global stability properties. Such an analysis via nonlinear control techniques may prove useful in several related over-parameterized problems.

Tradeoffs between convergence rate and noise amplification for momentum-based accelerated optimization algorithms

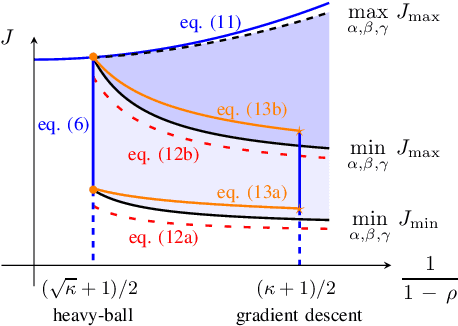
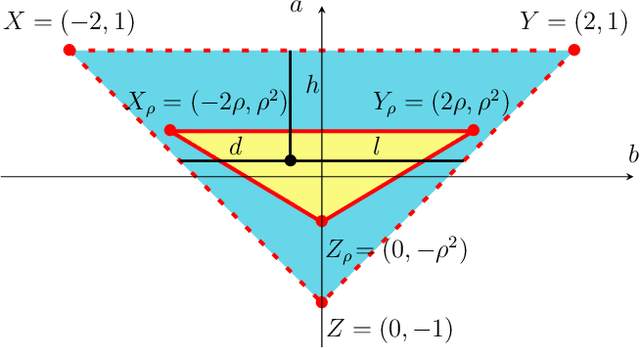
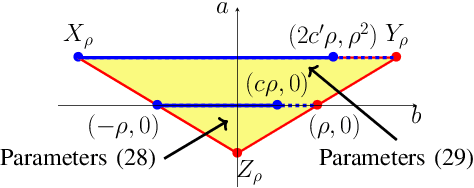
We study momentum-based first-order optimization algorithms in which the iterations utilize information from the two previous steps and are subject to an additive white noise. This class of algorithms includes heavy-ball and Nesterov's accelerated methods as special cases. For strongly convex quadratic problems, we use the steady-state variance of the error in the optimization variable to quantify noise amplification and exploit a novel geometric viewpoint to establish analytical lower bounds on the product between the settling time and the smallest/largest achievable noise amplification. For all stabilizing parameters, these bounds scale quadratically with the condition number. We also use the geometric insight developed in the paper to introduce two parameterized families of algorithms that strike a balance between noise amplification and settling time while preserving order-wise Pareto optimality. Finally, for a class of continuous-time gradient flow dynamics, whose suitable discretization yields two-step momentum algorithm, we establish analogous lower bounds that also scale quadratically with the condition number.

Transient growth of accelerated first-order methods for strongly convex optimization problems

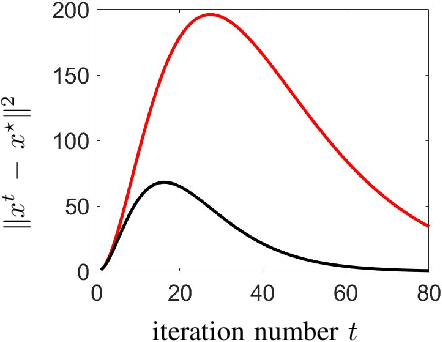
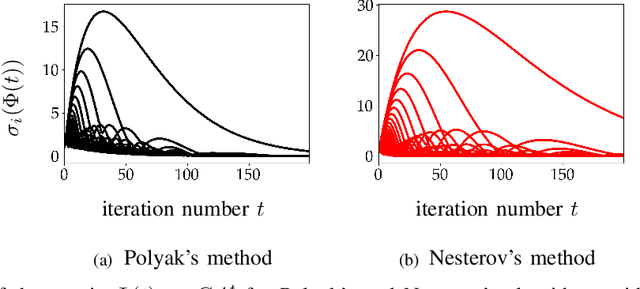
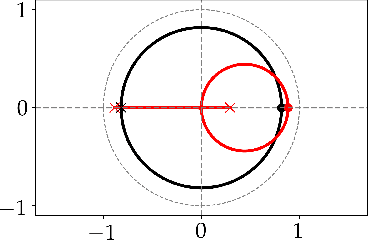
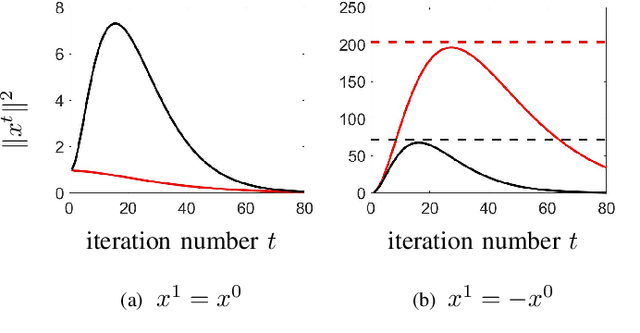
Optimization algorithms are increasingly being used in applications with limited time budgets. In many real-time and embedded scenarios, only a few iterations can be performed and traditional convergence metrics cannot be used to evaluate performance in these non-asymptotic regimes. In this paper, we examine the transient behavior of accelerated first-order optimization algorithms. For quadratic optimization problems, we employ tools from linear systems theory to show that transient growth arises from the presence of non-normal dynamics. We identify the existence of modes that yield an algebraic growth in early iterations and quantify the transient excursion from the optimal solution caused by these modes. For strongly convex smooth optimization problems, we utilize the theory of integral quadratic constraints to establish an upper bound on the magnitude of the transient response of Nesterov's accelerated method. We show that both the Euclidean distance between the optimization variable and the global minimizer and the rise time to the transient peak are proportional to the square root of the condition number of the problem. Finally, for problems with large condition numbers, we demonstrate tightness of the bounds that we derive up to constant factors.

Convergence and sample complexity of gradient methods for the model-free linear quadratic regulator problem

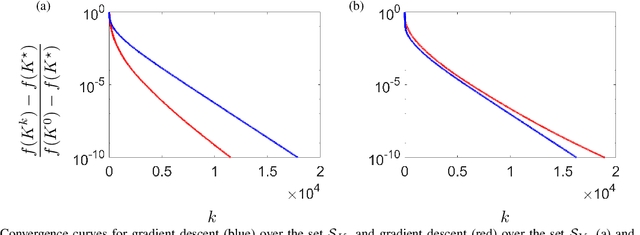
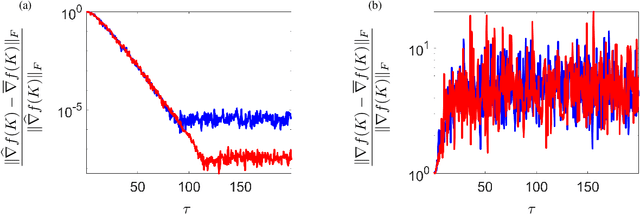
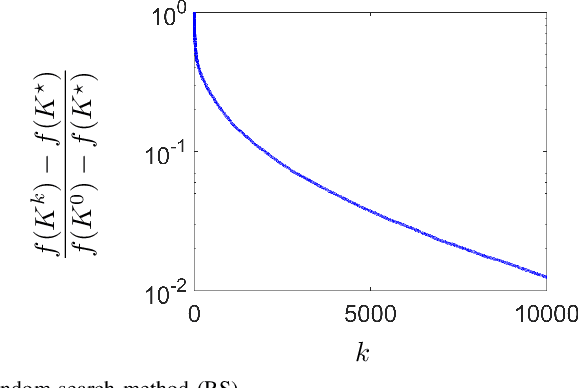
Model-free reinforcement learning attempts to find an optimal control action for an unknown dynamical system by directly searching over the parameter space of controllers. The convergence behavior and statistical properties of these approaches are often poorly understood because of the nonconvex nature of the underlying optimization problems as well as the lack of exact gradient computation. In this paper, we take a step towards demystifying the performance and efficiency of such methods by focusing on the standard infinite-horizon linear quadratic regulator problem for continuous-time systems with unknown state-space parameters. We establish exponential stability for the ordinary differential equation (ODE) that governs the gradient-flow dynamics over the set of stabilizing feedback gains and show that a similar result holds for the gradient descent method that arises from the forward Euler discretization of the corresponding ODE. We also provide theoretical bounds on the convergence rate and sample complexity of a random search method. Our results demonstrate that the required simulation time for achieving $\epsilon$-accuracy in a model-free setup and the total number of function evaluations both scale as $\log \, (1/\epsilon)$.

Robustness of accelerated first-order algorithms for strongly convex optimization problems

We study the robustness of accelerated first-order algorithms to stochastic uncertainties in gradient evaluation. Specifically, for unconstrained, smooth, strongly convex optimization problems, we examine the mean-square error in the optimization variable when the iterates are perturbed by additive white noise. This type of uncertainty may arise in situations where an approximation of the gradient is sought through measurements of a real system or in a distributed computation over network. Even though the underlying dynamics of first-order algorithms for this class of problems are nonlinear, we establish upper bounds on the mean-square deviation from the optimal value that are tight up to constant factors. Our analysis quantifies fundamental trade-offs between noise amplification and convergence rates obtained via any acceleration scheme similar to Nesterov's or heavy-ball methods. To gain additional analytical insight, for strongly convex quadratic problems we explicitly evaluate the steady-state variance of the optimization variable in terms of the eigenvalues of the Hessian of the objective function. We demonstrate that the entire spectrum of the Hessian, rather than just the extreme eigenvalues, influence robustness of noisy algorithms. We specialize this result to the problem of distributed averaging over undirected networks and examine the role of network size and topology on the robustness of noisy accelerated algorithms.