Tradeoffs between convergence rate and noise amplification for momentum-based accelerated optimization algorithms

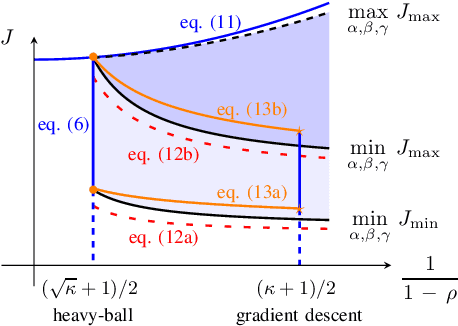
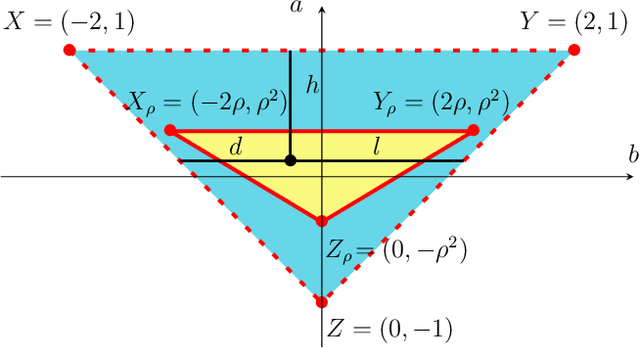
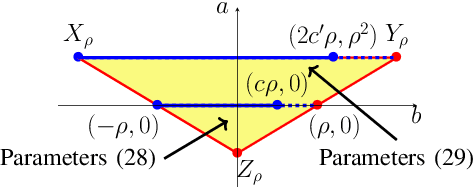
We study momentum-based first-order optimization algorithms in which the iterations utilize information from the two previous steps and are subject to an additive white noise. This class of algorithms includes heavy-ball and Nesterov's accelerated methods as special cases. For strongly convex quadratic problems, we use the steady-state variance of the error in the optimization variable to quantify noise amplification and exploit a novel geometric viewpoint to establish analytical lower bounds on the product between the settling time and the smallest/largest achievable noise amplification. For all stabilizing parameters, these bounds scale quadratically with the condition number. We also use the geometric insight developed in the paper to introduce two parameterized families of algorithms that strike a balance between noise amplification and settling time while preserving order-wise Pareto optimality. Finally, for a class of continuous-time gradient flow dynamics, whose suitable discretization yields two-step momentum algorithm, we establish analogous lower bounds that also scale quadratically with the condition number.